参考:https://www.luogu.org/blog/Owencodeisking/post-xue-xi-bi-ji-cdq-fen-zhi-hu-zheng-ti-er-fen
前置技能:树状数组,线段树,分治、归并排序
CDQ分治:
据说是OI大佬陈丹琦发明的
1.三维偏序
思路:
第一维排序,第二维分治,第三维树状数组上查询
考虑分治时区间 [l, m] 对区间 [m+1, r] 的贡献,因为第一维已经排好序,所以区间 [l, m] 的第一维小于区间 [m+1, r]的第一维
然后对于区间 [m+1, r]中的某个元素x,将区间 [l, m] 的第二维小于x的元素的按第三维的权值加入树状数组,
最后区间 [l, m] 对区间 x 的贡献就是查询树状数组中小于x第三维的个数
可以边进行分治边进行归并排序,树状数组要及时清空
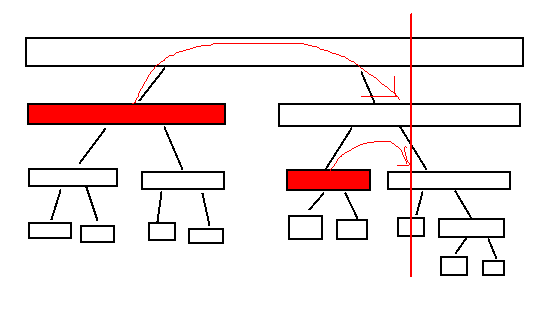
通过画图我们可以发现,对于每个位置,我们在分治时,它之前的位置对它的贡献都计算过了,所以这种方法是正确的。
因为递归的层数是log(n)层,再加上树状数组,所以时间复杂度是O(n*log(n)^2)
代码:
#pragma GCC optimize(2) #pragma GCC optimize(3) #pragma GCC optimize(4) #include<bits/stdc++.h> using namespace std; #define y1 y11 #define fi first #define se second #define pi acos(-1.0) #define LL long long #define ls rt<<1, l, m #define rs rt<<1|1, m+1, r //#define mp make_pair #define pb push_back #define ULL unsigned LL #define pll pair<LL, LL> #define pli pair<LL, int> #define pii pair<int, int> #define piii pair<pii, int> #define pdi pair<double, int> #define pdd pair<double, double> #define mem(a, b) memset(a, b, sizeof(a)) #define debug(x) cerr << #x << " = " << x << " "; #define fio ios::sync_with_stdio(false);cin.tie(0);cout.tie(0); //head const int N = 1e5 + 5, M = 2e5 + 5; struct Node { int x, y, z; int ans, cnt; bool operator < (const Node & rhs) const { if(x == rhs.x) { if(y == rhs.y) return z < rhs.z; else return y < rhs.y; } else return x < rhs.x; } }a[N], tmp[N]; int bit[M], res[N], n, k, cnt = 0; void add(int x, int a) { while(x <= k) bit[x] += a, x += x&-x; } int sum(int x) { int res = 0; while(x) res += bit[x], x -= x&-x; return res; } void cdq(int l, int r) { if(l == r) { a[l].ans += a[l].cnt-1; return ; } int m = l+r >> 1; cdq(l, m); cdq(m+1, r); int p = l, q = m+1, tp = l; while(q <= r) { while(p <= m && a[p].y <= a[q].y) add(a[p].z, a[p].cnt), tmp[tp++] = a[p], ++p; a[q].ans += sum(a[q].z); tmp[tp++] = a[q]; ++q; } for (int i = l; i < p; ++i) add(a[i].z, -a[i].cnt); while(p <= m) tmp[tp++] = a[p], ++p; for (int i = l; i <= r; ++i) a[i] = tmp[i]; } int main() { scanf("%d %d", &n, &k); for (int i = 1; i <= n; ++i) scanf("%d %d %d", &a[i].x, &a[i].y, &a[i].z); sort(a+1, a+1+n); int now = 1; for (int i = 2; i <= n; ++i) { if(a[i].x == a[i-1].x && a[i].y == a[i-1].y && a[i].z == a[i-1].z) ++now; else { a[++cnt] = a[i-1]; a[cnt].cnt = now; a[cnt].ans = 0; now = 1; } } a[++cnt] = a[n]; a[cnt].cnt = now; a[cnt].ans = 0; cdq(1, cnt); for (int i = 1; i <= cnt; ++i) res[a[i].ans] += a[i].cnt; for (int i = 0; i < n; ++i) printf("%d ", res[i]); return 0; }
思路:时间看成一个维度就转换成了三维偏序了
代码:

#pragma GCC optimize(2) #pragma GCC optimize(3) #pragma GCC optimize(4) #include<bits/stdc++.h> using namespace std; #define y1 y11 #define fi first #define se second #define pi acos(-1.0) #define LL long long #define ls rt<<1, l, m #define rs rt<<1|1, m+1, r //#define mp make_pair #define pb push_back #define ULL unsigned LL #define pll pair<LL, LL> #define pli pair<LL, int> #define pii pair<int, int> #define piii pair<pii, int> #define pdi pair<double, int> #define pdd pair<double, double> #define mem(a, b) memset(a, b, sizeof(a)) #define debug(x) cerr << #x << " = " << x << " "; #define fio ios::sync_with_stdio(false);cin.tie(0);cout.tie(0); //head const int N = 1e5 + 5; struct node { int a, t, x, ans, id; bool operator < (const node & rhs) const { return id < rhs.id; } }a[N], tmp[N]; int n; map<int, int> cnt; void cdq(int l, int r) { if(l == r) return ; int m = l+r >> 1; cdq(l, m); cdq(m+1, r); int p = l, q = m+1, tp = l; while(q <= r) { while(p <= m && a[p].t <= a[q].t) { if(a[p].a == 1) cnt[a[p].x]++; else if(a[p].a == 2) cnt[a[p].x]--; tmp[tp++] = a[p], ++p; } if(a[q].a == 3) a[q].ans += cnt[a[q].x]; tmp[tp++] = a[q]; ++q; } for (int i = l; i < p; ++i) { if(a[i].a == 1) cnt[a[i].x]--; else if(a[i].a == 2) cnt[a[i].x]++; } while(p <= m) tmp[tp++] = a[p], ++p; for (int i = l; i <= r; ++i) a[i] = tmp[i]; } int main() { scanf("%d", &n); for (int i = 1; i <= n; ++i) scanf("%d %d %d", &a[i].a, &a[i].t, &a[i].x), a[i].ans = 0, a[i].id = i; cdq(1, n); sort(a+1, a+1+n); for (int i = 1; i <= n; ++i) if(a[i].a == 3) printf("%d ", a[i].ans); return 0; }
例题2:HDU - 5618
思路:由于对于每个点都要询问,所以不能像陌上花开那样缩点了,排序后把相同的点的贡献先加上去
代码:

#pragma GCC optimize(2) #pragma GCC optimize(3) #pragma GCC optimize(4) #include<bits/stdc++.h> using namespace std; #define y1 y11 #define fi first #define se second #define pi acos(-1.0) #define LL long long #define ls rt<<1, l, m #define rs rt<<1|1, m+1, r //#define mp make_pair #define pb push_back #define ULL unsigned LL #define pll pair<LL, LL> #define pli pair<LL, int> #define pii pair<int, int> #define piii pair<pii, int> #define pdi pair<double, int> #define pdd pair<double, double> #define mem(a, b) memset(a, b, sizeof(a)) #define debug(x) cerr << #x << " = " << x << " "; #define fio ios::sync_with_stdio(false);cin.tie(0);cout.tie(0); //head const int N = 1e5 + 5; struct Node { int x, y, z, id; int cnt; bool operator < (const Node & rhs) const { if(x == rhs.x) { if(y == rhs.y) return z < rhs.z; else return y < rhs.y; } else return x < rhs.x; } }a[N], tmp[N]; int bit[N], ans[N], n, cnt = 0; void add(int x, int a) { while(x < N) bit[x] += a, x += x&-x; } int sum(int x) { int res = 0; while(x) res += bit[x], x -= x&-x; return res; } void cdq(int l, int r) { if(l == r) return ; int m = l+r >> 1; cdq(l, m); cdq(m+1, r); int p = l, q = m+1, tp = l; while(q <= r) { while(p <= m && a[p].y <= a[q].y) add(a[p].z, a[p].cnt), tmp[tp++] = a[p], ++p; ans[a[q].id] += sum(a[q].z); tmp[tp++] = a[q]; ++q; } for (int i = l; i < p; ++i) add(a[i].z, -a[i].cnt); while(p <= m) tmp[tp++] = a[p], ++p; for (int i = l; i <= r; ++i) a[i] = tmp[i]; } int T; int main() { scanf("%d", &T); while(T--) { scanf("%d", &n); for (int i = 1; i <= n; ++i) scanf("%d %d %d", &a[i].x, &a[i].y, &a[i].z), a[i].id = i, a[i].cnt = 1, ans[i] = 0; sort(a+1, a+1+n); int now = 0; for (int i = n-1; i >= 1; --i) { if(a[i].x == a[i+1].x && a[i].y == a[i+1].y && a[i].z == a[i+1].z) ++now; else now = 0; ans[a[i].id] += now; } cdq(1, n); for (int i = 1; i <= n; ++i) printf("%d ", ans[i]); } return 0; }
例题3:CodeChef - QRECT
思路:考虑用容斥,用总个数减去和横纵坐标和它不相交的个数,这样我们发现和它横纵坐标都不相交被减了两次,也就是四个角上的矩形,四个角上的矩形的个数就是三维偏序问题
代码:

#include<bits/stdc++.h> using namespace std; #define y1 y11 #define pb push_back //head const int N = 1e5 + 10, M = 2e5 + 5; struct Node { int ty, x1, y1, x2, y2, id; int ans, cnt; bool operator < (const Node & rhs) const { return id < rhs.id; } }a[N], aa[N], tmp[N]; vector<int> vx, vy; int n, bit1[M], bit2[M], bit[M], p, pos[N], cnt = 0, now = 0; char op[10]; void add(int x, int a, int *bit) { while(x < M) bit[x] += a, x += x&-x; } int sum(int x, int *bit) { int res = 0; while(x) res += bit[x], x -= x&-x; return res; } void init() { for (int i = 1; i < M; ++i) bit1[i] = bit2[i] = 0; } void cdq1(int l, int r) { if(l == r) return ; int m = l+r >> 1; cdq1(l, m); cdq1(m+1, r); int p = l, q = m+1, tp = l; while(q <= r) { while(p <= m && aa[p].x1 < aa[q].x1) { if(aa[p].ty == 1) add(aa[p].y1, 1, bit); else if(aa[p].ty == 2) add(aa[p].y1, -1, bit); tmp[tp++] = aa[p]; ++p; } if(aa[q].ty == 3) { aa[q].ans += sum(aa[q].y1-1, bit); } tmp[tp++] = aa[q]; ++q; } for (int i = l; i < p; ++i) if(aa[i].ty == 1) add(aa[i].y1, -1, bit); else if(aa[i].ty == 2) add(aa[i].y1, 1, bit); while(p <= m) tmp[tp++] = aa[p], ++p; for (int i = l; i <= r; ++i) aa[i] = tmp[i]; } void cdq2(int l, int r) { if(l == r) return ; int m = l+r >> 1; cdq2(l, m); cdq2(m+1, r); int p = l, q = m+1, tp = l; while(q <= r) { while(p <= m && aa[p].x1 > aa[q].x1) { if(aa[p].ty == 1) add(aa[p].y1, 1, bit); else if(aa[p].ty == 2) add(aa[p].y1, -1, bit); tmp[tp++] = aa[p]; ++p; } if(aa[q].ty == 3) { aa[q].ans += sum(M-1, bit) - sum(aa[q].y1, bit); } tmp[tp++] = aa[q]; ++q; } for (int i = l; i < p; ++i) if(aa[i].ty == 1) add(aa[i].y1, -1, bit); else if(aa[i].ty == 2) add(aa[i].y1, 1, bit); while(p <= m) tmp[tp++] = aa[p], ++p; for (int i = l; i <= r; ++i) aa[i] = tmp[i]; } void cdq3(int l, int r) { if(l == r) return ; int m = l+r >> 1; cdq3(l, m); cdq3(m+1, r); int p = l, q = m+1, tp = l; while(q <= r) { while(p <= m && aa[p].x1 < aa[q].x1) { if(aa[p].ty == 1) add(aa[p].y1, 1, bit); else if(aa[p].ty == 2) add(aa[p].y1, -1, bit); tmp[tp++] = aa[p]; ++p; } if(aa[q].ty == 3) { aa[q].ans += sum(M-1, bit) - sum(aa[q].y1, bit); } tmp[tp++] = aa[q]; ++q; } for (int i = l; i < p; ++i) if(aa[i].ty == 1) add(aa[i].y1, -1, bit); else if(aa[i].ty == 2) add(aa[i].y1, 1, bit); while(p <= m) tmp[tp++] = aa[p], ++p; for (int i = l; i <= r; ++i) aa[i] = tmp[i]; } void cdq4(int l, int r) { if(l == r) return ; int m = l+r >> 1; cdq4(l, m); cdq4(m+1, r); int p = l, q = m+1, tp = l; while(q <= r) { while(p <= m && aa[p].x1 > aa[q].x1) { if(aa[p].ty == 1) add(aa[p].y1, 1, bit); else if(aa[p].ty == 2) add(aa[p].y1, -1, bit); tmp[tp++] = aa[p]; ++p; } if(aa[q].ty == 3) { aa[q].ans += sum(aa[q].y1-1, bit); } tmp[tp++] = aa[q]; ++q; } for (int i = l; i < p; ++i) if(aa[i].ty == 1) add(aa[i].y1, -1, bit); else if(aa[i].ty == 2) add(aa[i].y1, 1, bit); while(p <= m) tmp[tp++] = aa[p], ++p; for (int i = l; i <= r; ++i) aa[i] = tmp[i]; } int main() { scanf("%d", &n); for (int i = 1; i <= n; ++i) { scanf("%s", op); if(op[0] == 'I') { scanf("%d %d %d %d", &a[i].x1, &a[i].y1, &a[i].x2, &a[i].y2); if(a[i].x1 > a[i].x2) swap(a[i].x1, a[i].x2); if(a[i].y1 > a[i].y2) swap(a[i].y1, a[i].y2); vx.pb(a[i].x1);vx.pb(a[i].x2);vy.pb(a[i].y1);vy.pb(a[i].y2); a[i].ty = 1; a[i].id = i; pos[++now] = i; ++cnt; } else if(op[0] == 'D') { scanf("%d", &p); a[i] = a[pos[p]]; a[i].ty = 2; a[i].id = i; --cnt; } else { scanf("%d %d %d %d", &a[i].x1, &a[i].y1, &a[i].x2, &a[i].y2); if(a[i].x1 > a[i].x2) swap(a[i].x1, a[i].x2); if(a[i].y1 > a[i].y2) swap(a[i].y1, a[i].y2); vx.pb(a[i].x1);vx.pb(a[i].x2);vy.pb(a[i].y1);vy.pb(a[i].y2); a[i].ty = 3; a[i].id = i; a[i].cnt = a[i].ans = cnt; } } sort(vx.begin(), vx.end()); vx.erase(unique(vx.begin(), vx.end()), vx.end()); sort(vy.begin(), vy.end()); vy.erase(unique(vy.begin(), vy.end()), vy.end()); for (int i = 1; i <= n; ++i) { a[i].x1 = lower_bound(vx.begin(), vx.end(), a[i].x1) - vx.begin() + 1; a[i].x2 = lower_bound(vx.begin(), vx.end(), a[i].x2) - vx.begin() + 1; a[i].y1 = lower_bound(vy.begin(), vy.end(), a[i].y1) - vy.begin() + 1; a[i].y2 = lower_bound(vy.begin(), vy.end(), a[i].y2) - vy.begin() + 1; } for (int i = 1; i <= n; ++i) { if(a[i].ty == 1) add(a[i].x1, 1, bit1), add(a[i].x2, 1, bit2); else if(a[i].ty == 2) add(a[i].x1, -1, bit1), add(a[i].x2, -1, bit2); else a[i].ans -= sum(a[i].x1-1, bit2) + (sum(M-1, bit1) - sum(a[i].x2, bit1)); } init(); for (int i = 1; i <= n; ++i) { if(a[i].ty == 1) add(a[i].y1, 1, bit1), add(a[i].y2, 1, bit2); else if(a[i].ty == 2) add(a[i].y1, -1, bit1), add(a[i].y2, -1, bit2); else a[i].ans -= sum(a[i].y1-1, bit2) + (sum(M-1, bit1) - sum(a[i].y2, bit1)); } for (int i = 1; i <= n; ++i) { aa[i] = a[i]; if(a[i].ty <= 2) aa[i].x1 = a[i].x2, aa[i].y1 = a[i].y2; } cdq1(1, n); sort(aa+1, aa+1+n); for (int i = 1; i <= n; ++i) a[i].ans = aa[i].ans; for (int i = 1; i <= n; ++i) { aa[i] = a[i]; if(a[i].ty == 3) aa[i].x1 = a[i].x2, aa[i].y1 = a[i].y2; } cdq2(1, n); sort(aa+1, aa+1+n); for (int i = 1; i <= n; ++i) a[i].ans = aa[i].ans; for (int i = 1; i <= n; ++i) { aa[i] = a[i]; if(a[i].ty <= 2) aa[i].x1 = a[i].x2, aa[i].y1 = a[i].y1; else aa[i].x1 = a[i].x1, aa[i].y1 = a[i].y2; } cdq3(1, n); sort(aa+1, aa+1+n); for (int i = 1; i <= n; ++i) a[i].ans = aa[i].ans; for (int i = 1; i <= n; ++i) { aa[i] = a[i]; if(a[i].ty <= 2) aa[i].x1 = a[i].x1, aa[i].y1 = a[i].y2; else aa[i].x1 = a[i].x2, aa[i].y1 = a[i].y1; } cdq4(1, n); sort(aa+1, aa+1+n); for (int i = 1; i <= n; ++i) a[i].ans = aa[i].ans; for (int i = 1; i <= n; ++i) if(a[i].ty == 3) printf("%d ", a[i].ans); return 0; }
思路:将删除的时间看成一个维度
代码:

#include<bits/stdc++.h> using namespace std; #define LL long long const int N = 1e5 + 5; struct Node { int t, v, pos, id; bool operator < (const Node & rhs) const { return t < rhs.t; } }a[N], tmp[N]; int pos[N], ans[N], n, m, b; LL res = 0; struct BIT { int bit[N]; void init() { for (int i = 1; i <= n; ++i) bit[i] = 0; } void add(int x, int a) { while(x <= n) bit[x] += a, x += x&-x; } int sum(int x) { int res = 0; while(x) res += bit[x], x -= x&-x; return res; } }B; void cdq1(int l, int r) { if(l == r) return ; int m = l+r >> 1; cdq1(l, m); cdq1(m+1, r); int p = l, q = m+1, tp = l; while(q <= r) { while(p <= m && a[p].pos < a[q].pos) { B.add(a[p].v, 1); tmp[tp++] = a[p]; ++p; } ans[a[q].id] += B.sum(n) - B.sum(a[q].v); tmp[tp++] = a[q]; ++q; } for (int i = l; i < p; ++i) B.add(a[i].v, -1); while(p <= m) tmp[tp++] = a[p], ++p; for (int i = l; i <= r; ++i) a[i] = tmp[i]; } void cdq2(int l, int r) { if(l == r) return ; int m = l+r >> 1; cdq2(l, m); cdq2(m+1, r); int p = l, q = m+1, tp = l; while(q <= r) { while(p <= m && a[p].pos > a[q].pos) { B.add(a[p].v, 1); tmp[tp++] = a[p]; ++p; } ans[a[q].id] += B.sum(a[q].v-1); tmp[tp++] = a[q]; ++q; } for (int i = l; i < p; ++i) B.add(a[i].v, -1); while(p <= m) tmp[tp++] = a[p], ++p; for (int i = l; i <= r; ++i) a[i] = tmp[i]; } int main() { scanf("%d %d", &n, &m); for (int i = 1; i <= n; ++i) { scanf("%d", &a[i].v); a[i].pos = i; a[i].id = 0; a[i].t = 0; pos[a[i].v] = i; } for (int i = 1; i <= n; ++i) { res += B.sum(n) - B.sum(a[i].v); B.add(a[i].v, 1); } B.init(); for (int i = 1; i <= m; ++i) { scanf("%d", &b); a[pos[b]].id = i; a[pos[b]].t = m-i+1; } sort(a+1, a+1+n); cdq1(1, n); sort(a+1, a+1+n); cdq2(1, n); for (int i = 1; i <= m; ++i) { printf("%lld ", res); res -= ans[i]; } return 0; }
例题5:UVALive - 6667
思路:严格三维偏序,在对x排序时,如果x相同,按y从大到小排序,这样x相同是左边区间就不会对右边区间产生贡献了,因为这时左边y大于等于右边y
代码:

#pragma GCC optimize(2) #pragma GCC optimize(3) #pragma GCC optimize(4) #include<bits/stdc++.h> using namespace std; #define y1 y11 #define fi first #define se second #define pi acos(-1.0) #define LL long long #define ls rt<<1, l, m #define rs rt<<1|1, m+1, r //#define mp make_pair #define pb push_back #define ULL unsigned LL #define pll pair<LL, LL> #define pli pair<LL, int> #define pii pair<int, int> #define piii pair<pii, int> #define pdi pair<double, int> #define pdd pair<double, double> #define mem(a, b) memset(a, b, sizeof(a)) #define debug(x) cerr << #x << " = " << x << " "; #define fio ios::sync_with_stdio(false);cin.tie(0);cout.tie(0); //head const int N = 3e5 + 10, MM = 1e6 + 5; struct Node { int x, y, z, len; }a[N]; struct BIT { int bit[MM]; void clr(int x) { while(x < MM) bit[x] = 0, x += x&-x; } void add(int x, int a) { while(x < MM) bit[x] = max(bit[x], a), x += x&-x; } int mx(int x) { int res = 0; while(x) res = max(res, bit[x]), x -= x&-x; return res; } }b; bool cmp1(Node a, Node b) { if(a.x == b.x) return a.y > b.y; else return a.x < b.x; } bool cmp2(Node a, Node b) { return a.y < b.y; } void cdq(int l, int r) { if(l == r) return ; int m = l+r >> 1; cdq(l, m); sort(a+l, a+m+1, cmp2); sort(a+m+1, a+r+1, cmp2); int p = l, q = m+1; while(q <= r) { while(p <= m && a[p].y < a[q].y) b.add(a[p].z, a[p].len), ++p; a[q].len = max(a[q].len, b.mx(a[q].z-1)+1); ++q; } for (int i = l; i < p; ++i) b.clr(a[i].z); sort(a+m+1, a+r+1, cmp1); cdq(m+1, r); } int A, B, C = ~(1<<31), M = (1<<16)-1, m, n; int r() { A = 36969 * (A & M) + (A >> 16); B = 18000 * (B & M) + (B >> 16); return (C & ((A << 16) + B)) % 1000000; } int main() { while(~scanf("%d %d %d %d", &m, &n, &A, &B)) { if(!m && !n && !A && !B) break; for (int i = 1; i <= m; ++i) { scanf("%d %d %d", &a[i].x, &a[i].y, &a[i].z); a[i].z++; a[i].len = 1; } for (int i = 1; i <= n; ++i) { ++m; a[m].x = r(); a[m].y = r(); a[m].z = r(); a[m].z++; a[m].len = 1; } sort(a+1, a+1+m, cmp1); cdq(1, m); int ans = 1; for (int i = 1; i <= m; ++i) ans = max(ans, a[i].len); printf("%d ", ans); } return 0; }
2.四维偏序
参考:http://www.cnblogs.com/candy99/p/6442434.html
cdq套cdq
假设四维为(a, b, c, d),在进行普通的cdq分治时,我们归并排序使得b有序,这个时候就可以再套一个cdq来解决(b, c, d)的三维偏序问题,但是这时不要忘记了a的作用,
我们要求a有序时左边[l, m]对右边[m+1, r]的贡献,所以在套之前给左边[l, m]的元素打个标记来区分,然后就可以愉快地套cdq了。时间复杂度显然为O(n*log(n)^3)。
然后原题找不到了,做一道稍微复杂点的,不要忘记第二个cdq是在新数组上进行,如果在原数组上进行的话,做完以后b就不是有序的了。
思路:将一个查询用容斥拆分成8个查询
代码:
#pragma GCC optimize(2) #pragma GCC optimize(3) #pragma GCC optimize(4) #include<bits/stdc++.h> using namespace std; #define y1 y11 #define fi first #define se second #define pi acos(-1.0) #define LL long long #define ls rt<<1, l, m #define rs rt<<1|1, m+1, r //#define mp make_pair #define pb push_back #define ULL unsigned LL #define pll pair<LL, LL> #define pli pair<LL, int> #define pii pair<int, int> #define piii pair<pii, int> #define pdi pair<double, int> #define pdd pair<double, double> #define mem(a, b) memset(a, b, sizeof(a)) #define debug(x) cerr << #x << " = " << x << " "; #define fio ios::sync_with_stdio(false);cin.tie(0);cout.tie(0); //head const int N = 5e4 + 5; struct Node { int ty, x, y, z, c, id; bool flag; }a[N*8], t1[N*8], t2[N*8]; vector<int> vc; int T, n, ty, x1, y1, z1, x2, y2, z2, tot = 0, ans[N], cnt = 0, sz; struct BIT { int bit[N*8]; void add(int x, int a) { while(x <= sz) bit[x] += a, x += x&-x; } int sum(int x) { int res = 0; while(x) res += bit[x], x -= x&-x; return res; } }B; void cdq1(int l, int r){ if(l == r) return ; int m = l+r >> 1; cdq1(l, m); cdq1(m+1, r); int p = l, q = m+1, tp = l; Node *a = t1, *t = t2; while(q <= r) { while(p <= m && a[p].y <= a[q].y) { if(a[p].flag && a[p].ty == 1) B.add(a[p].z, 1); t[tp++] = a[p]; ++p; } if(!a[q].flag && a[q].ty == 2) ans[a[q].id] += a[q].c*B.sum(a[q].z); t[tp++] = a[q]; ++q; } for (int i = l; i < p; ++i) if(a[i].flag && a[i].ty == 1) B.add(a[i].z, -1); while(p <= m) t[tp++] = a[p], ++p; for (int i = l; i <= r; ++i) a[i] = t[i]; } void cdq(int l, int r) { if(l == r) return ; int m = l+r >> 1; cdq(l, m); cdq(m+1, r); int p = l, q = m+1, tp = l; Node *t = t1; while(q <= r) { while(p <= m && a[p].x <= a[q].x) t[tp] = a[p], t[tp].flag = 1, ++tp, ++p; t[tp] = a[q]; t[tp].flag = 0; ++tp; ++q; } while(p <= m) t[tp] = a[p], t[tp].flag = 1, ++tp, ++p; for (int i = l; i <= r; ++i) a[i] = t[i]; cdq1(l, r); } int main() { scanf("%d", &T); while(T--) { scanf("%d", &n); tot = cnt = 0; for (int i = 1; i <= n; ++i) { scanf("%d", &ty); if(ty == 1) { ++tot; a[tot].ty = 1; scanf("%d %d %d", &a[tot].x, &a[tot].y, &a[tot].z); } else { scanf("%d %d %d %d %d %d", &x1, &y1, &z1, &x2, &y2, &z2); ++cnt; ans[cnt] = 0; a[++tot] = {2, x2, y2, z2, 1, cnt, 0}; a[++tot] = {2, x1-1, y2, z2, -1, cnt, 0}; a[++tot] = {2, x2, y1-1, z2, -1, cnt, 0}; a[++tot] = {2, x2, y2, z1-1, -1, cnt, 0}; a[++tot] = {2, x1-1, y1-1, z2, 1, cnt, 0}; a[++tot] = {2, x1-1, y2, z1-1, 1, cnt, 0}; a[++tot] = {2, x2, y1-1, z1-1, 1, cnt, 0}; a[++tot] = {2, x1-1, y1-1, z1-1, -1, cnt, 0}; } } vc.clear(); for (int i = 1; i <= tot; ++i) vc.pb(a[i].z); sort(vc.begin(), vc.end()); vc.erase(unique(vc.begin(), vc.end()), vc.end()); for (int i = 1; i <= tot; ++i) a[i].z = lower_bound(vc.begin(), vc.end(), a[i].z) - vc.begin()+1; sz = (int)vc.size(); cdq(1, tot); for (int i = 1; i <= cnt; ++i) printf("%d ", ans[i]); } return 0; }
3.其他
cdq优化dp等。
例题1:HYSBZ - 4553
思路:设mx[i]为第i个的最大值,mn[i]为最小值
dp[i] = max{dp[j] + 1} 其中 j < i, mx[j] <= a[i], a[j] <= mn[i]
这是个三维偏序问题,可以用cdq维护dp的转移,具体看代码:

#pragma GCC optimize(2) #pragma GCC optimize(3) #pragma GCC optimize(4) #include<bits/stdc++.h> using namespace std; #define y1 y11 #define fi first #define se second #define pi acos(-1.0) #define LL long long #define ls rt<<1, l, m #define rs rt<<1|1, m+1, r //#define mp make_pair #define pb push_back #define ULL unsigned LL #define pll pair<LL, LL> #define pli pair<LL, int> #define pii pair<int, int> #define piii pair<pii, int> #define pdi pair<double, int> #define pdd pair<double, double> #define mem(a, b) memset(a, b, sizeof(a)) #define debug(x) cerr << #x << " = " << x << " "; #define fio ios::sync_with_stdio(false);cin.tie(0);cout.tie(0); //head const int N = 1e5 + 5; struct Node { int v, mx, mn, id, dp; }a[N]; struct BIT { int bit[N]; void clr(int x) { while(x < N) bit[x] = 0, x += x&-x; } void add(int x, int a) { while(x < N) bit[x] = max(bit[x], a), x += x&-x; } int mx(int x) { int res = 0; while(x) res = max(res, bit[x]), x -= x&-x; return res; } }b; bool cmp1(Node a, Node b) { return a.mx < b.mx; } bool cmp2(Node a, Node b) { return a.v < b.v; } bool cmp3(Node a, Node b) { return a.id < b.id; } void cdq(int l, int r) { if(l == r) return ; int m = l+r >> 1; cdq(l, m); sort(a+l, a+m+1, cmp1); sort(a+m+1, a+r+1, cmp2); int p = l, q = m+1; while(q <= r) { while(p <= m && a[p].mx <= a[q].v) b.add(a[p].v, a[p].dp), ++p; a[q].dp = max(a[q].dp, b.mx(a[q].mn)+1); ++q; } for (int i = l; i < p; ++i) b.clr(a[i].v); sort(a+m+1, a+r+1, cmp3); cdq(m+1, r); } int n, m, x, y; int main() { scanf("%d %d", &n, &m); for (int i = 1; i <= n; ++i) { scanf("%d", &a[i].v); a[i].mn = a[i].mx = a[i].v; a[i].id = i; a[i].dp = 1; } for (int i = 1; i <= m; ++i) { scanf("%d %d", &x, &y); a[x].mx = max(a[x].mx, y); a[x].mn = min(a[x].mn, y); } cdq(1, n); int ans = 1; for (int i = 1; i <= n; ++i) ans = max(ans, a[i].dp); printf("%d ", ans); return 0; }
例题2:HDU - 4742
思路:同样是dp,用bit维护最大值和最大值的个树,有点小技巧
代码:

#pragma GCC optimize(2) #pragma GCC optimize(3) #pragma GCC optimize(4) #include<bits/stdc++.h> using namespace std; #define y1 y11 #define fi first #define se second #define pi acos(-1.0) #define LL long long #define ls rt<<1, l, m #define rs rt<<1|1, m+1, r //#define mp make_pair #define pb push_back #define ULL unsigned LL #define pll pair<LL, LL> #define pli pair<LL, int> #define pii pair<int, int> #define piii pair<pii, int> #define pdi pair<double, int> #define pdd pair<double, double> #define mem(a, b) memset(a, b, sizeof(a)) #define debug(x) cerr << #x << " = " << x << " "; #define fio ios::sync_with_stdio(false);cin.tie(0);cout.tie(0); //head const int N = 1e5 + 10; struct Node { int x, y, z, len, cnt; }a[N]; vector<int> vc; int T, n, sz; struct BIT { pii bit[N]; void modify(pii &a, pii b) { if(b.fi == a.fi) a.se += b.se; else if(b.fi > a.fi) a = b; } void clr(int x) { while(x <= sz) bit[x] = {0, 0}, x += x&-x; } void add(int x, pii a) { while( x <= sz) modify(bit[x], a), x += x&-x; } pii mx(int x) { pii res = {0, 0}; while(x) modify(res, bit[x]), x -= x&-x; return res; } }b; bool cmp1(Node a, Node b) { return a.x < b.x; } bool cmp2(Node a, Node b) { return a.y < b.y; } pii MX(pii a, pii b) { if(a.fi == b.fi) return {a.fi, a.se+b.se}; else if(a.fi > b.fi) return a; else return b; } void cdq(int l, int r) { if(l == r) return ; int m = l+r >> 1; cdq(l, m); sort(a+l, a+m+1, cmp2); sort(a+m+1, a+r+1, cmp2); int p = l, q = m+1; while(q <= r) { while(p <= m && a[p].y <= a[q].y) b.add(a[p].z, {a[p].len, a[p].cnt}), ++p; pii t1 = b.mx(a[q].z); t1.fi++; pii t2 = MX({a[q].len, a[q].cnt}, t1); a[q].len = t2.fi, a[q].cnt = t2.se; ++q; } for (int i = l; i < p; ++i) b.clr(a[i].z); sort(a+m+1, a+r+1, cmp1); cdq(m+1, r); } int main() { scanf("%d", &T); while(T--) { scanf("%d", &n); vc.clear(); for (int i = 1; i <= n; ++i) { scanf("%d %d %d", &a[i].x, &a[i].y, &a[i].z); vc.pb(a[i].z); a[i].len = a[i].cnt = 1; } sort(vc.begin(), vc.end()); vc.erase(unique(vc.begin(), vc.end()), vc.end()); for (int i = 1; i <= n; ++i) a[i].z = lower_bound(vc.begin(), vc.end(), a[i].z) - vc.begin() + 1; sz = (int)vc.size(); sort(a+1, a+1+n, cmp1); cdq(1, n); pii ans = {0, 0}; for (int i = 1; i <= n; ++i) ans = MX(ans, {a[i].len, a[i].cnt}); printf("%d %d ", ans.fi, ans.se); } return 0; }
例题3:HDU - 5324
思路:由于要求字典序最小,所以要求dp[i]:以i为起点的最长上升序列,cdq的话先求右边再求左边
代码:

#pragma GCC optimize(2) #pragma GCC optimize(3) #pragma GCC optimize(4) #include<bits/stdc++.h> using namespace std; #define y1 y11 #define fi first #define se second #define pi acos(-1.0) #define LL long long #define ls rt<<1, l, m #define rs rt<<1|1, m+1, r //#define mp make_pair #define pb push_back #define ULL unsigned LL #define pll pair<LL, LL> #define pli pair<LL, int> #define pii pair<int, int> #define piii pair<pii, int> #define pdi pair<double, int> #define pdd pair<double, double> #define mem(a, b) memset(a, b, sizeof(a)) #define debug(x) cerr << #x << " = " << x << " "; #define fio ios::sync_with_stdio(false);cin.tie(0);cout.tie(0); //head const int N = 5e4 + 5; struct Node { int L, R, id; }a[N]; vector<int> vc, res; int sz, n, dp[N], pre[N]; struct BIT { pii bit[N]; void clr(int x) { while(x <= sz) bit[x] = {0, 0}, x += x&-x; } void add(int x, pii a) { while(x <= sz) { if(a.fi > bit[x].fi) bit[x] = a; else if(a.fi == bit[x].fi && a.se < bit[x].se) bit[x] = a; x += x&-x; } } pii mx(int x) { pii res = {0, 0}; while(x) { if(bit[x].fi > res.fi) res = bit[x]; else if(bit[x].fi == res.fi && bit[x].se < res.se) res = bit[x]; x -= x&-x; } return res; } }b; bool cmp1(const Node &a, const Node &b) { return a.id < b.id; } bool cmp2(const Node &a, const Node &b) { return a.R > b.R; } void cdq(int l, int r) { if(l == r) return ; int m = l+r >> 1; cdq(m+1, r); sort(a+l, a+m+1, cmp2); sort(a+m+1, a+r+1, cmp2); int p = l, q = m+1; while(p <= m) { while(q <= r && a[q].R >= a[p].R) b.add(a[q].L, {dp[a[q].id], a[q].id}), ++q; pii P = b.mx(a[p].L); if(P.fi+1 > dp[a[p].id]) { dp[a[p].id] = P.fi+1; pre[a[p].id] = P.se; } else if(P.fi+1 == dp[a[p].id] && P.se < pre[a[p].id]) pre[a[p].id] = P.se; ++p; } for (int i = m+1; i < q; ++i) b.clr(a[i].L); sort(a+l, a+m+1, cmp1); cdq(l, m); } int main() { while(~scanf("%d", &n)) { vc.clear(); for (int i = 1; i <= n; ++i) scanf("%d", &a[i].L), vc.pb(a[i].L); for (int i = 1; i <= n; ++i) scanf("%d", &a[i].R); sort(vc.begin(), vc.end()); vc.erase(unique(vc.begin(), vc.end()), vc.end()); sz = (int)vc.size(); for (int i = 1; i <= n; ++i) { a[i].id = i; dp[i] = 1; pre[i] = 0; a[i].L = lower_bound(vc.begin(), vc.end(), a[i].L) - vc.begin() + 1; } cdq(1, n); res.clear(); int mx = 0, pe = 0; res.pb(0); for (int i = 1; i <= n; ++i) { if(dp[i] > mx) { mx = dp[i]; pe = pre[i]; res[0] = i; } } printf("%d ", mx); while(pe) { res.pb(pe); pe = pre[pe]; } for (int i = 0; i < mx; ++i) printf("%d%c", res[i], " "[i==mx-1]); } return 0; }
参考:https://www.cnblogs.com/Sakits/p/7990875.html
整体二分:
1.静态区间第k大
思路:首先对于单个查询我们可以二分答案求解,对于一个二分出来的mid,如果我们能知道小于等于mid的个数,就能判断答案是小于等于mid还是大于mid
整体二分就是将所有查询的二分放在一起考虑,如果对于某个查询我们能快速知道小于等于mid的个数(可以用树状数组维护,将小于等于mid的修改按位置加入),
我们就能知道哪些查询答案是小于等于mid,哪些查询答案是大于mid,哪些修改只对答案小于等于mid的查询有用,哪些修改只对答案大于mid的查询有用
按照这个标准将所有查询修改分成两部分,递归求解,直到二分答案的区间长度为1。具体实现看代码(l,r表示二分答案的区间,L,R表示查询或修改的区间)
时间复杂度:与cdq分治类似,为O(n*log(n)^2)
代码:
#pragma GCC optimize(2) #pragma GCC optimize(3) #pragma GCC optimize(4) #include<iostream> #include<cstdio> #include<algorithm> using namespace std; #define y1 y11 #define fi first #define se second #define pi acos(-1.0) #define LL long long #define ls rt<<1, l, m #define rs rt<<1|1, m+1, r //#define mp make_pair #define pb push_back #define ULL unsigned LL #define pll pair<LL, LL> #define pli pair<LL, int> #define pii pair<int, int> #define piii pair<pii, int> #define pdi pair<double, int> #define pdd pair<double, double> #define mem(a, b) memset(a, b, sizeof(a)) #define debug(x) cerr << #x << " = " << x << " "; #define fio ios::sync_with_stdio(false);cin.tie(0);cout.tie(0); //head const int N = 1.1e5 + 5; const int INF = 0x3f3f3f3f; struct Node { int ty, x, y, k, id; }a[N], t1[N], t2[N]; int n, m, ans[N]; struct BIT { int bit[N]; inline void add(int x, int a) { while(x < N) bit[x] += a, x += x&-x; } inline int sum(int x) { int res = 0; while(x) res += bit[x], x -= x&-x; return res; } }b; void solve(int l, int r, int L, int R) { if(l > r || L > R) return ; if(l == r) { for (int i = L; i <= R; ++i) if(a[i].ty == 2) ans[a[i].id] = l; return ; } int m = l+r >> 1; int p = 0, q = 0; for (int i = L; i <= R; ++i) { if(a[i].ty == 2){ int cnt = b.sum(a[i].y) - b.sum(a[i].x-1); if(cnt >= a[i].k) t1[++p] = a[i]; else a[i].k -= cnt, t2[++q] = a[i]; } else { if(a[i].x <= m) b.add(a[i].id, 1), t1[++p] = a[i]; else t2[++q] = a[i]; } } for (int i = 1; i <= p; ++i) if(t1[i].ty == 1) b.add(t1[i].id, -1); for (int i = 1; i <= p; ++i) a[L+i-1] = t1[i]; for (int i = 1; i <= q; ++i) a[L+p+i-1] = t2[i]; solve(l, m, L, L+p-1); solve(m+1, r, L+p, R); } int main() { scanf("%d %d", &n, &m); for (int i = 1; i <= n; ++i) { scanf("%d", &a[i].x); a[i].ty = 1; a[i].id = i; } for (int i = n+1; i <= n+m; ++i) { scanf("%d %d %d", &a[i].x, &a[i].y, &a[i].k); a[i].ty = 2; a[i].id = i-n; } solve(-INF, INF, 1, n+m); for (int i = 1; i <= m; ++i) printf("%d ", ans[i]); return 0; }
2.动态第k大
思路:在静态第k大的基础上将修改拆成两个,具体看代码
代码:
#pragma GCC optimize(2) #pragma GCC optimize(3) #pragma GCC optimize(4) #include<iostream> #include<cstdio> #include<algorithm> using namespace std; #define y1 y11 #define fi first #define se second #define pi acos(-1.0) #define LL long long #define ls rt<<1, l, m #define rs rt<<1|1, m+1, r //#define mp make_pair #define pb push_back #define ULL unsigned LL #define pll pair<LL, LL> #define pli pair<LL, int> #define pii pair<int, int> #define piii pair<pii, int> #define pdi pair<double, int> #define pdd pair<double, double> #define mem(a, b) memset(a, b, sizeof(a)) #define debug(x) cerr << #x << " = " << x << " "; #define fio ios::sync_with_stdio(false);cin.tie(0);cout.tie(0); //head const int N = 1e5 + 5; const int INF = 0x3f3f3f3f; struct Node { int ty, x, y, k, id; }q[N], t1[N], t2[N]; int n, m, a[N], ans[N]; struct BIT { int bit[N]; inline void add(int x, int a) { while(x <= n) bit[x] += a, x += x&-x; } inline int sum(int x) { int res = 0; while(x) res += bit[x], x -= x&-x; return res; } }b; void solve(int l, int r, int L, int R) { if(l > r || L > R) return ; if(l == r) { for (int i = L; i <= R; ++i) if(q[i].ty == 2) ans[q[i].id] = l; return ; } int m = l+r >> 1, c1 = 0, c2 = 0; for (int i = L; i <= R; ++i) { if(q[i].ty == 2) { int cnt = b.sum(q[i].y) - b.sum(q[i].x-1); if(q[i].k <= cnt) t1[++c1] = q[i]; else q[i].k -= cnt, t2[++c2] = q[i]; } else { if(q[i].x <= m) b.add(q[i].id, q[i].y), t1[++c1] = q[i]; else t2[++c2] = q[i]; } } for (int i = 1; i <= c1; ++i) if(t1[i].ty == 1) b.add(t1[i].id, -t1[i].y); for (int i = 1; i <= c1; ++i) q[L+i-1] = t1[i]; for (int i = 1; i <= c2; ++i) q[L+c1+i-1] = t2[i]; solve(l, m, L, L+c1-1); solve(m+1, r, L+c1, R); } int T, x, y, k; char op[10]; int main() { scanf("%d", &T); while(T--) { scanf("%d %d", &n, &m); int tot = 0; for (int i = 1; i <= n; ++i) { scanf("%d", &a[i]); q[++tot] = {1, a[i], 1, 0, i}; } for (int i = 1; i <= m; ++i) { scanf("%s", op); if(op[0] == 'Q') { scanf("%d %d %d", &x, &y, &k); q[++tot] = {2, x, y, k, i}; } else { scanf("%d %d", &x, &y); q[++tot] = {1, a[x], -1, 0, x}; q[++tot] = {1, a[x]=y, 1, 0, x}; } ans[i] = -1; } solve(0, INF, 1, tot); for (int i = 1; i <= m; ++i) if(~ans[i]) printf("%d ", ans[i]); } return 0; }
例题1:HYSBZ - 3110
思路:在线段树上进行区间加法
代码:

#pragma GCC optimize(2) #pragma GCC optimize(3) #pragma GCC optimize(4) #include<bits/stdc++.h> using namespace std; #define y1 y11 #define fi first #define se second #define pi acos(-1.0) #define LL long long #define ls rt<<1, l, m #define rs rt<<1|1, m+1, r //#define mp make_pair #define pb push_back #define ULL unsigned LL #define pll pair<LL, LL> #define pli pair<LL, int> #define pii pair<int, int> #define piii pair<pii, int> #define pdi pair<double, int> #define pdd pair<double, double> #define mem(a, b) memset(a, b, sizeof(a)) #define debug(x) cerr << #x << " = " << x << " "; #define fio ios::sync_with_stdio(false);cin.tie(0);cout.tie(0); //head const int N = 5e4 + 5; struct Node { int ty, x, y, id; LL c; }a[N], t1[N], t2[N]; int n, m, ans[N]; LL tree[N<<2], lazy[N<<2]; inline void push_up(int rt) { tree[rt] = tree[rt<<1] + tree[rt<<1|1]; } inline void push_down(int rt, int len) { lazy[rt<<1] += lazy[rt]; lazy[rt<<1|1] += lazy[rt]; tree[rt<<1] += lazy[rt]*(len - (len>>1)); tree[rt<<1|1] += lazy[rt]*(len>>1); lazy[rt] = 0; } void update(int L, int R, int x, int rt, int l, int r) { if(L <= l && r <= R) { lazy[rt] += x; tree[rt] += x*(r-l+1); return ; } if(lazy[rt]) push_down(rt, r-l+1); int m = l+r >> 1; if(L <= m) update(L, R, x, ls); if(R > m) update(L, R, x, rs); push_up(rt); } LL query(int L, int R, int rt, int l, int r) { if(L <= l && r <= R) return tree[rt]; if(lazy[rt]) push_down(rt, r-l+1); int m = l+r >> 1; LL ans = 0; if(L <= m) ans += query(L, R, ls); if(R > m) ans += query(L, R, rs); push_up(rt); return ans; } void solve(int l, int r, int L, int R) { if(l > r || L > R) return ; if(l == r) { for (int i = L; i <= R; ++i) if(a[i].ty == 2) ans[a[i].id] = l; return ; } int m = l+r >> 1, p = 0, q = 0; for (int i = L; i <= R; ++i) { if(a[i].ty == 2) { LL cnt = query(a[i].x, a[i].y, 1, 1, n); if(cnt >= a[i].c) t2[++q] = a[i]; else a[i].c -= cnt, t1[++p] = a[i]; } else { if(a[i].c > m) update(a[i].x, a[i].y, 1, 1, 1, n), t2[++q] = a[i]; else t1[++p] = a[i]; } } for (int i = 1; i <= q; ++i) if(t2[i].ty == 1) update(t2[i].x, t2[i].y, -1, 1, 1, n); for (int i = 1; i <= p; ++i) a[L+i-1] = t1[i]; for (int i = 1; i <= q; ++i) a[L+p+i-1] = t2[i]; solve(l, m, L, L+p-1); solve(m+1, r, L+p, R); } int tot = 0; int main() { scanf("%d %d", &n, &m); for (int i = 1; i <= m; ++i) scanf("%d %d %d %lld", &a[i].ty, &a[i].x, &a[i].y, &a[i].c), a[i].id = (a[i].ty == 1)?i:(++tot); solve(-n, n, 1, m); for (int i = 1; i <= tot; ++i) printf("%d ", ans[i]); return 0; }
思路:在二维树状数组上进行加法
代码:

#include<bits/stdc++.h> using namespace std; #define y1 y11 #define LL long long const int N = 505, M = 3.2e5 + 5; const int INF = 0x3f3f3f3f; struct Node { int ty, x1, y1, x2, y2, k, id; }a[M], t1[M], t2[M]; int n, m, ans[M]; struct BIT2 { int bit[N][N]; inline void add(int x, int y, int a) { for (int i = x; i <= n; i += i&-i) { for (int j = y; j <= n; j += j&-j) { bit[i][j] += a; } } } inline int sum(int x, int y) { int res = 0; for (int i = x; i > 0; i -= i&-i) { for (int j = y; j > 0; j -= j&-j) { res += bit[i][j]; } } return res; } }B; void solve(int l, int r, int L, int R){ if(l > r || L > R) return ; if(l == r) { for (int i = L; i <= R; ++i) { if(a[i].ty == 2) ans[a[i].id] = l; } return ; } int m = l+r >> 1, p = 0, q = 0; for (int i = L; i <= R; ++i) { if(a[i].ty == 1) { if(a[i].k <= m) B.add(a[i].x1, a[i].y1, 1), t1[++p] = a[i]; else t2[++q] = a[i]; } else { int cnt = B.sum(a[i].x2, a[i].y2) - B.sum(a[i].x1-1, a[i].y2) - B.sum(a[i].x2, a[i].y1-1) + B.sum(a[i].x1-1, a[i].y1-1); if(cnt >= a[i].k) t1[++p] = a[i]; else a[i].k -= cnt, t2[++q] = a[i]; } } for (int i = 1; i <= p; ++i) if(t1[i].ty == 1) B.add(t1[i].x1, t1[i].y1, -1); for (int i = 1; i <= p; ++i) a[L+i-1] = t1[i]; for (int i = 1; i <= q; ++i) a[L+p+i-1] = t2[i]; solve(l, m, L, L+p-1); solve(m+1, r, L+p, R); } int main() { int tot = 0; scanf("%d %d", &n, &m); for (int i = 1; i <= n; ++i) { for (int j = 1; j <= n; ++j) { ++tot; scanf("%d", &a[tot].k); a[tot].x1 = i; a[tot].y1 = j; a[tot].ty = 1; } } for (int i = 1; i <= m; ++i) { ++tot; scanf("%d %d %d %d %d", &a[tot].x1, &a[tot].y1, &a[tot].x2, &a[tot].y2, &a[tot].k); a[tot].ty = 2; a[tot].id = i; } solve(-INF, INF, 1, tot); for (int i = 1; i <= m; ++i) printf("%d ", ans[i]); return 0; }
