Codeforces 385D

385D - Bear and Floodlight

思路：状态压缩dp+计算几何。

i表示亮灯的集合，i的二进制中1表示亮灯，0表示不亮灯。

dp[i]表示在i的亮灯情况下最大的可以照亮的长度。

状态转移方程：dp[i^(1<<j)]=max(dp[i^(1<<j)],cal(dp[i],j))。

其中i&(1 << j)=0表示第j个灯不在i状态中，然后把第j个灯的照射范围放在最右边，cal(dp[i],j)求出第j个灯从dp[i]位置开始照可以照多长的距离。

最终dp[(1 << n)-1]即为答案。

关于cal函数的计算，见下图（还有两种情况没有画）：

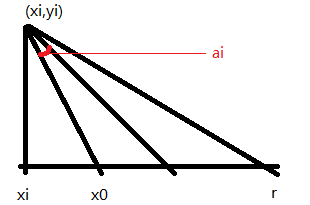
代码：

#include<bits/stdc++.h>
using namespace std;
#define ll long long
#define pb push_back
#define mem(a,b) memset((a),(b),sizeof(a))
#define pi acos(-1.0)
double x[20],y[20],a[20],dp[(1<<20)-1];
double l,r;
double cal(double x0,int i)
{
    double t1=atan((r-x[i])/y[i]);
    double t2=atan((x0-x[i])/y[i])+a[i];
    return x[i]+tan(min(t1,t2))*y[i];
}

int main()
{
    ios::sync_with_stdio(false);
    cin.tie(0);
    int n;
    cin>>n>>l>>r;
    r-=l;
    for(int i=0;i<n;i++)
    {
        cin>>x[i]>>y[i]>>a[i];
        x[i]-=l;
        a[i]=a[i]/180.*pi;
    }
    
    int N=1<<n;
    for(int i=0;i<N;i++)
    {
        for(int j=0;j<n;j++)
        {
            if((i&(1<<j))==0)
            {
                dp[i^(1<<j)]=max(dp[i^(1<<j)],cal(dp[i],j));
            }
        }
    }
    cout<<fixed<<setprecision(10)<<dp[N-1]<<endl;
    return 0;
}