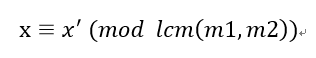算法笔记--中国剩余定理

中国剩余定理（CRT）的表述如下

设正整数两两互素，则同余方程组

                             

有整数解。并且在模下的解是唯一的，解为

                               

其中，而为模的逆元。

模板：

int ex_gcd(int a,int b,int &x,int &y)
{
    if(b==0)
    {
        x=1;
        y=0;
        return a;
    }
    int ans=ex_gcd(b,a%b,y,x);
    y-=a/b*x;
    return ans;
}
int CRT(int a[],int m[],int n)
{
    int M=1;
    int ans=0;
    for(int i=1;i<=n;i++)M*=m[i];
    for(int i=1;i<=n;i++)
    {
        int x,y;
        int Mi=M/m[i];
        ex_gcd(Mi,m[i],x,y); 
        ans=(ans+a[i]*Mi*x)%M;
    }
    if(ans<0)ans+=M;
    return ans;
}

例题1:ZSTUOJ 1265: Biorhythms

代码：

#include<bits/stdc++.h>
using namespace std;
#define ll long long
#define pb push_back
#define mem(a,b) memset(a,b,sizeof(a))

int a[10],m[10];
int ex_gcd(int a,int b,int &x,int &y)
{
    if(b==0)
    {
        x=1;
        y=0;
        return a;
    }
    int ans=ex_gcd(b,a%b,y,x);
    y-=a/b*x;
    return ans;
}
int CRT(int a[],int m[],int n)
{
    int M=1;
    int ans=0;
    for(int i=1;i<=n;i++)M*=m[i];
    for(int i=1;i<=n;i++)
    {
        int x,y;
        int Mi=M/m[i];
        ex_gcd(Mi,m[i],x,y); 
        ans=(ans+a[i]*Mi*x)%M;
    }
    if(ans<0)ans+=M;
    return ans;
}
int main()
{
    ios::sync_with_stdio(false);
    cin.tie(0);
    int p,e,i,d;
    int cse=1;
    while(cin>>p>>e>>i>>d)
    {
        if(p==-1&&e==-1&&i==-1)break;
        a[1]=p%23;
        a[2]=e%28;
        a[3]=i%33;
        m[1]=23;
        m[2]=28;
        m[3]=33;
        int ans=CRT(a,m,3);
        if(ans<=d)ans+=21252;
        cout<<"Case "<<cse++<<": the next triple peak occurs in "<<ans-d<<" days."<<endl;
    }
    return 0; 
} 

例题2：

中国剩余定理扩展——求解模数不互质情况下的线性方程组：

　　普通的中国剩余定理要求所有的互素，那么如果不互素呢，怎么求解同余方程组？

　　这种情况就采用两两合并的思想，假设要合并如下两个方程：

                  

　　那么得到：

    

　　我们需要求出一个最小的xx使它满足：

                 

　　那么x1和x2就要尽可能的小，于是我们用扩展欧几里得算法求出x1x1的最小正整数解，将它代回a1+m1，得到x的一个特解x′，当然也是最小正整数解。

　　所以xx的通解一定是x′x′加上lcm(m1,m2)∗k，这样才能保证x模m1和m2的余数是a1和a2。由此，我们把这个x′当做新的方程的余数，把lcm(m1,m2)l当做新的方程的模数。（这一段是关键）

                 

　　参考：https://www.cnblogs.com/MashiroSky/p/5918158.html