【LeetCode & 剑指offer 刷题笔记】目录(持续更新中...)
排列与组合
说明:排列组合方法很多,不限于文中的这些方法,可以在网上多看些解法,选择几种自己比较欣赏的解法。
1 Permutations I
Given a collection of distinct integers, return all possible permutations.
Example:
Permutations I问题
Input: [1,2,3]
Output:
[
[1,2,3],
[1,3,2],
[2,1,3],
[2,3,1],
[3,1,2],
[3,2,1]
]
Permutations II问题
Input: [1,1,2]
Output:
[
[1,1,2],
[1,2,1],
[2,1,1]
]
/*问题: next_permutation ??单个元素如果大于9还适用吗??(有时间在讨论)
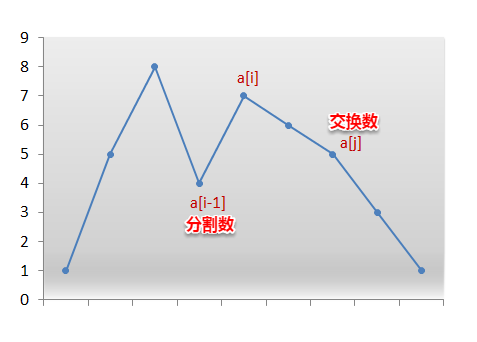
找下一个排列数,这里将排列位上的各位构成数字,下一种排列,其排列数大于输入排列数(如果输入的数为降序,已经最大,则约定下一个排列为升序排列,回到最小排列数),其最接近
要得到某个排列数下一个最接近的排列数
方法:具体见note
最小的排列数为增序排列,最大的排列数为降序排列,中间的为乱序,
(1) 先找第一个分割数pivot,其满足小于后一个相邻数,且最靠后(可以从后往前扫描)
(2) 再到后面找一个刚好大于此分割数的数changenum(从后往前扫描)
(3) 交换pivot与changenum
(4) 反序pivot后面的序列
例:
6 8 7 4 3 2
[6] 8 [7] 4 3 2 选中pivot和changenum
[7] 8 [6] 4 3 2 交换
7 [8 6 4 3 2]
7 [2 3 4 6 8] 反序pivot+1~end的序列
*/


//排列与组合问题示例:字符串的排列
//返回一个数组所有可能的排列结果(数组中所有元素不同) 方法一也适用于Permutations II
//可以看成回溯法,也可以看成暴力枚举法
//方法一:偷懒法 stl中next_permutation函数
//O(n!), O(1)
#include <algorithm>
class Solution
{
public:
vector<vector<int>> permute(vector<int>& nums)
{
vector<vector<int>> result;
sort(nums.begin(), nums.end()); //排列成增序
do
{
result.push_back(nums);
}while(next_permutation(nums.begin(), nums.end()));
//若新排列按字典序大于旧者则为 true 。若抵达最后重排并重置范围为首个排列则为 false
return result;
}
};
//方法二:自己实现 next_permutation
#include <algorithm>
class Solution
{
public:
vector<vector<int>> permute(vector<int>& nums)
{
vector<vector<int>> result;
sort(nums.begin(), nums.end()); //排列成增序
do
{
result.push_back(nums);
}while(nextPermutation(nums)); //与系统默认的函数参数不同
//若新排列按字典序大于旧者则为 true 。若抵达最后重排并重置范围为首个排列则为 false
return result;
}
public:
//O(n),O(1)
bool nextPermutation(vector<int>& nums)
{
if(nums.empty() || nums.size()==1) return false; //异常情况处理
int pivot = -1; //初始化枢轴
for(int i = nums.size()-1; i>=1; i--) //从后往前扫描,找到分割数
{
if(nums[i-1] < nums[i])
{
pivot = i-1;
break;
}
}
if(pivot == -1) //说明排列数已经最大,不存在分割数
{
reverse(nums.begin(), nums.end());
return false; //排列数已经最大时,返回false
}
int change = pivot; //初始化changenum位置
for(int i = nums.size()-1; i>=0; i--) //从后往前扫描,找changenum
{
if(nums[i] > nums[pivot])
{
change = i;
break;
}
}
swap(nums[pivot], nums[change]); //交换
reverse(nums.begin()+pivot+1, nums.end()); //反序(注意这里是begin()+pivot+1,对应索引为pivot+1的位置)
return true; //存在下一个排列数
}
};
/*
方法三:递归法
*/
#include <algorithm>
class Solution
{
public:
vector<vector<int> > permute(vector<int>& num)
{
vector<vector<int>> result;
if(num.empty()) return result;
vector<int> path; //中间结果
sort(num.begin(), num.end()); //sort之后递归函数才能按全排列顺序排列(好的初始顺序)
dfs(num, path, result);
return result;
}
private:
void dfs(vector<int>& num, vector<int>& path, vector<vector<int>>& result)
{
if(path.size() == num.size())
{
result.push_back(path);
return;
}
for(int a:num) //用于产生递归树某一层的多个分支,if语句来约束分支
{
if(find(path.begin(), path.end(), a) == path.end()) //如果在当前路径上没有元素a,则将该元素push到路径
{
path.push_back(a);
dfs(num, path, result); //产生递归树的深度
path.pop_back(); //回溯,腾出空间,供一个分支push元素
}
}
}
};
2 Permutations II
Given a collection of numbers that might contain duplicates, return all possible unique permutations.
Example:
Input: [1,1,2]
Output:
[
[1,1,2],
[1,2,1],
[2,1,1]
]
//返回一个数组所有可能的排列结果(数组中存在重复元素)
/*
方法一:用next_permutation ,同问题Permutations 1
*/
/*
方法二:dfs
用一个map来统计各个元素出现的次数,通过这个容器约束各路径
与问题Permutations 1不同的是现在用计数器来约束,而之前用输入的num数组来约束选取(递归函数for循环部分)
*/
#include <map>
class Solution
{
public:
vector<vector<int>> permuteUnique(vector<int>& nums)
{
vector<vector<int>> result;
if(nums.empty()) return result;
vector<int> path;
map<int,int> counter;
// sort(str.begin(), str.end()); //上面用了map,故这里无需先sort了
for(int a:nums) counter[a]++; //统计nums中各数出现的次数没有key的时候会自动创建
dfs(nums, counter, path, result);//递归
return result;
}
private:
void dfs(vector<int>& nums, map<int,int>& counter, vector<int>& path, vector<vector<int>>& result)
{
if(path.size() == nums.size()) //到达树的末尾,将单路径数组push到结果向量中
{
result.push_back(path);
return;
}
for(auto& p:counter) //for循环带来的是树宽度方向的延伸,即产生同一层的多个分支
{
if(p.second>0) //如果该元素没有被取完(某个元素可能会出现多次)
{
path.push_back(p.first);
p.second--; //已经取了这个元素,统计数减一
dfs(nums, counter, path, result); //继续往深度方向延伸
path.pop_back(); //回溯,给其他分支腾空间!!
p.second++;
}
}
}
};
3 Combinations
Given two integers n and k, return all possible combinations of k numbers out of 1 ... n.
Example:
Input: n = 4, k = 2
Output:
[
[2,4],
[3,4],
[2,3],
[1,2],
[1,3],
[1,4],
]
//产生所有可能组合(给n和k,返回从1~n中k个数的组合)
/*
递归法:画出递归树(数的组合数),然后设计递归函数
举例,1~4,k=3
(为了避免重复,后面的数都必须必前面的大)
dfs(3) push and return
dfs(2) dfs(4) push and return
dfs(1) dfs(3) dfs(4) push and return
dfs(4) return(递归子程序结束)
dfs(2)....
dfs(3)...
dfs(4)...
*/
class Solution
{
public:
vector<vector<int>> combine(int n, int k)
{
vector<vector<int>> result;
vector<int> path;
if(n<=0 || k<=0) return result;
dfs(n, k, 1, path, result);
return result;
}
private:
//start为每个父结点的子结点开始的数,子结点取nums[start~end]
//到树的末尾后push到result中
void dfs(int n, int k, int start, vector<int>& path, vector<vector<int>>& result)
{
if(path.size() == k) //步数达到k后push路径,步数达不到k的,会运行到for循环,函数末尾而结束(递归到start = n时就会结束)
{
result.push_back(path);
return; //递归出口之一
}
for(int i = start; i<=n; i++) //产生父结点的多个子结点
{
path.push_back(i);
dfs(n, k, i+1, path, result); //深度方向和宽度方向都是以i~end扩展,而记录深度变化,通过step
(为了避免重复,后面的数都必须必前面的大)某分支下一个step的start = i+1
path.pop_back(); //腾出空间
}
}
};