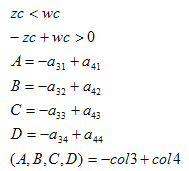3、使用裁剪空间的方法提取平面
上一篇中,我们讨论了通过几何的方法提取视锥体的六个片面。在这一篇中,我们继续讨论通过裁剪空间的方法来提取视锥体的平面。
假设现在在世界坐标系中有一点p=(x,yz,1),modelview矩阵记作M,projection矩阵记作P。当点p经过这两个矩阵变换后变到pc=(xc,yc,zc,wc)的位置,即
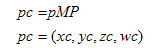
因为pc点是由齐次坐标表示的,则其正则化后为pcn:
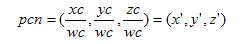
在正则化的裁剪空间中,视锥体的中心与单位立方体的原点对齐,且它的六个平面由以下平面界定:
- Left Plane: x’ = -1
- Right Plane: x’ = 1
- Top Plane: y’ = 1
- Bottom Plane: y’ = -1
- Near Plane: z’ = -1
- Far Plane: z’ = 1
那么,当pcn=(x',y',z')的坐标满足以下关系时,就证明pcn在视锥体内部:
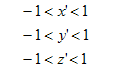
往前推一步,没有正则化的pc=(xc,yc,zc),如果想在视锥体内的话,那它的坐标范围为:
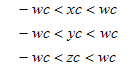
基于这样的信息,那么我们就可以用世界坐标来届定六个平面,例如,当pc点在左平面的“右”侧时,就必须满足:
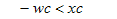
继续向前推一步,考虑点p的坐标,记A=MP,如下图所示
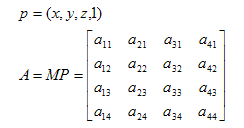
点pc中xc和wc坐标就可以通过以下式子计算:
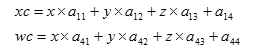
则p点在视锥体左平面的右侧就可以用以下不等式表示:
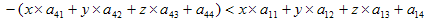
经过如下简单代数变换:
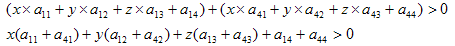
就可以得到左平面的一般方程:(Ax+By+Cz+D=0)
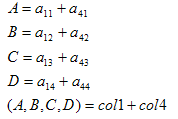
其中,col1和col4分别代表A矩阵的第一列和第四列。
如果我们只需要考虑一个点在平面左还是右,那上面的定义已经足够了,但是在后面我们还要检测球体在平面的左侧还是右侧,这需要计算球心到平面的距离。就还需要对平面进行一般化,即求出其一般方程。
右平面也可以通过同样地方式获得:
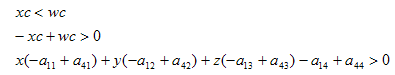
右平面方程的系数:
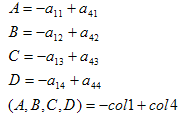
剩余的平面:
下平面
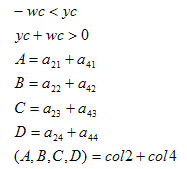
上平面

近平面
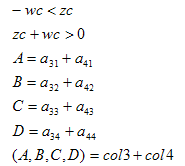
远平面