写在最前面:
这一寒假,因为假期的延长,学习了一下新的算法和数据结构。可能有些完全掌握了,但是有些确实有些不熟练。
在假期的最后一段时间,我会将在寒假及之前学习的一些知识逐渐整理为笔记,供自己复习巩固,也供他人学习了解。笔记的顺序按照我学习该知识点的时间排序。
笔记大部分会写的很详细,面向初学者还是很好懂的。虽然我的语文不好,但我会尽量用我的最好水平来写。
可能一个学 OI 还不到半年的蒟蒻的笔记确实没有什么看的价值,但我还是希望和大家一起慢慢变强。OI 的路还很长,一步一步走下去吧。
希望在某一天开学后,没有人后悔自己一整个寒假碌碌无为。
1.快速幂
目录:
-
什么是快速幂
-
快速幂的原理
-
快速幂的代码实现
-
快速幂的位运算优化
什么是快速幂?
快速幂是一种快速求幂的算法,面对大量数据时就会展现出它的优势。
朴素的求幂算法是用一个循环逐渐累乘,时间复杂度为 (Theta(n)),(n) 为指数。代码如下:
#define mod 10000007
long long power(long long base,long long n)
{
long long res=1;
for(register long long i=1;i<=n;++i)
res*=base,res%=mod;
return res;
}
但是在处理正整数次幂时,可以使用一种时间复杂度为 (Theta(log_2n)) 的算法,就是我们要用的快速幂。
快速幂的原理
快速幂的思想是将指数拆分为若干个 (2) 次幂之和,然后分别进行计算。
为什么这样更快呢?我们想一下,如果在循环中乘上本身而不是乘上底数,即可得到若干的 (2) 次幂,求 (2^i) 次幂的时间复杂度就是 (Theta(i)),而朴素的算法为 (Theta(2^i))。
那么怎么将十进制转换为二进制?不会的人请看下面。
我们举一个例子,我们要求 (a) 的 (11) 次幂。
我们将 (11) 转换为二进制数:
我们发现二进制中,数字为 (1) 的数位为第 (0) 位、第 (1) 位和第 (3) 位,分别对应 (2^0,2^1,2^3),而 (11) 正好等于 (2^0+2^1+2^3)。
其实上述做法就是十进制转二进制最常用的方法:按权展开。
因此,并根据同底数幂乘法原理:
就可以实现用若干 (2) 次幂来表示指数再进行计算了。
快速幂的代码实现
如何用代码实现呢?一般有循环和递归两种。
while 循环实现
一般常用此方法,因为循环效率比递归高,个人也较喜欢此方法。下面的详细解释也以此方法为例。
在 while 循环中,指数不为 (0) 为循环条件,每次循环中将底数扩方,相应的指数除以 (2)。在遇到奇数时,代表一个二次幂分解完,将答案乘上当前的底数。
代码:
#define mod 10000007
long long qpower(long long base,long long n) //base 为底数,n 为指数。
{
long long res=1; //res 为幂。
while(n>0)
{
if(n%2==1)
res=res*base%mod;
base=base*base%mod;
n/=2;
}
return res;
}
结合 Dev-c++ 的调试功能我们可以更清楚的了解实现的过程,我们以计算 (2^5) 为例:
进入循环,初始赋值:
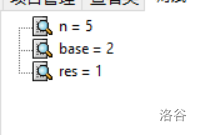
此时 (n) 为奇数,更新 res。同时更改 base(底数)、n(指数):

然后的 (n) 为偶数,res 不作操作,其他同上。
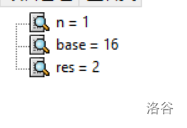
这是就是最后一次了,(n) 为 (1),最后一次更新。

然后 (n) 变成了 (0),跳出循环,此时 res 为 (32)。
递归实现:
递归实现的思路其实和循环是一样的,我在这里就简单的贴一个代码:
#define mod 10000007
long long qpower(long long base,long long n)
{
if(n==0)
return 1;
if(n==1)
return base;
long long res=qpower(base,n/2)%mod;
res=res*res%mod;
if(n%2==1)
res=res*base%mod;
return res;
}
快速幂的位运算优化
前置知识:位运算基础。
我们知道,计算机有一个很神奇的运算,叫做位运算,它比普通运算快许多,那在快速幂中能不能用位运算优化呢?
肯定是能的。
首先 >> 表示右移,a>>i 表示将 (a) 在二进制下右移 (i) 位,低位丢弃。那么不难想到,n/2 就可以用 n>>1 来代替。
那么在判定奇偶性时怎么用位运算优化呢?首先,我们知道,如果一个数是奇数,那么它在二进制下,末位一定是 (1)。根据这个特点,我们可以用按位与 &这种运算来代替。
我们知道,(1) 的二进制数是 (0000ldots 0001),那么将它和一个奇数按位与,结果肯定是 (0000ldots 0001),转为十进制就是 (1),偶数则为 (0)。因此,代码中的 n%2==1 可以改为 n&1。
优化过的代码:
#define mod 10000007
long long qpower(long long base,long long n)
{
long long res=1;
while(n>0)
{
if(n&1)
res=res*base%mod;
base=base*base%mod;
n>>=1;
}
return res;
}
后记
这是第一篇笔记,可能有很多不足,我会逐渐改进。希望能越来越好吧。