5道巧妙位操作的算法题。
***第一道***
题目描述
给定一个非空整数数组,除了某个元素只出现一次以外,其余每个元素均出现两次。找出那个只出现了一次的元素。
说明:
你的算法应该具有线性时间复杂度。 你可以不使用额外空间来实现吗?
示例 1:
输入: [2,2,1] 输出: 1
示例 2:
输入: [4,1,2,1,2] 输出: 4
题目解析
根据题目描述,由于加上了时间复杂度必须是O(n),并且空间复杂度为O(1)的条件,因此不能用排序方法,也不能使用map数据结构。
小吴想了一下午没想出来,答案是使用 位操作Bit Operation 来解此题。
将所有元素做异或运算,即a[1] ⊕ a[2] ⊕ a[3] ⊕ …⊕ a[n],所得的结果就是那个只出现一次的数字,时间复杂度为O(n)。
异或
异或运算A ⊕ B的真值表如下:
AB⊕FFFFTTTFTTTF
动画演示
进阶版
有一个 n 个元素的数组,除了两个数只出现一次外,其余元素都出现两次,让你找出这两个只出现一次的数分别是几,要求时间复杂度为 O(n) 且再开辟的内存空间固定(与 n 无关)。
示例 :
输入: [1,2,2,1,3,4] 输出: [3,4]
题目再解析
根据前面找一个不同数的思路算法,在这里把所有元素都异或,那么得到的结果就是那两个只出现一次的元素异或的结果。
然后,因为这两个只出现一次的元素一定是不相同的,所以这两个元素的二进制形式肯定至少有某一位是不同的,即一个为 0 ,另一个为 1 ,现在需要找到这一位。
根据异或的性质 任何一个数字异或它自己都等于 0,得到这个数字二进制形式中任意一个为 1 的位都是我们要找的那一位。
再然后,以这一位是 1 还是 0 为标准,将数组的 n 个元素分成两部分。
- 将这一位为 0 的所有元素做异或,得出的数就是只出现一次的数中的一个
- 将这一位为 1 的所有元素做异或,得出的数就是只出现一次的数中的另一个。
这样就解出题目。忽略寻找不同位的过程,总共遍历数组两次,时间复杂度为O(n)。
动画再演示
***第二道***
题目来源于 LeetCode 上第 231 号问题:2 的幂。题目难度为 Easy,目前通过率为 45.6% 。
题目描述
给定一个整数,编写一个函数来判断它是否是 2 的幂次方。
示例 1:
输入: 1
输出: true
解释: 20 = 1
示例 2:
输入: 16
输出: true
解释: 24 = 16
示例 3:
输入: 218
输出: false
题目解析
首先,先来分析一下 2 的次方数的二进制写法:

仔细观察,可以看出 2 的次方数都只有一个 1 ,剩下的都是 0 。根据这个特点,只需要每次判断最低位是否为 1 ,然后向右移位,最后统计 1 的个数即可判断是否是 2 的次方数。
代码很简单:
class Solution { public: bool isPowerOfTwo(int n) { int cnt = 0; while (n > 0) { cnt += (n & 1); n >>= 1; } return cnt == 1; } };
该题还有一种巧妙的解法。再观察上面的表格,如果一个数是 2 的次方数的话,那么它的二进数必然是最高位为1,其它都为 0 ,那么如果此时我们减 1 的话,则最高位会降一位,其余为 0 的位现在都为变为 1,那么我们把两数相与,就会得到 0。
比如 2 的 3 次方为 8,二进制位 1000 ,那么 8 - 1 = 7,其中 7 的二进制位 0111。
图片描述

代码实现
利用这个性质,只需一行代码就可以搞定。
1 class Solution { 2 public: 3 bool isPowerOfTwo(int n) { 4 return (n > 0) && (!(n & (n - 1))); 5 } 6 };
***第三道***
### 题目描述
给定一个整数 (32 位有符号整数),请编写一个函数来判断它是否是 4 的幂次方。
示例 1:
输入: 16
输出: true
示例 2:
输入: 5
输出: false
进阶:
你能不使用循环或者递归来完成本题吗?
题目解析
这道题最直接的方法就是不停的去除以 4 ,看最终结果是否为 1 ,参见代码如下:
1 class Solution { 2 public boolean isPowerOfFour(int num) { 3 while ( (num != 0) && (num % 4 == 0)) { 4 num /= 4; 5 } 6 return num == 1; 7 } 8 }
不过这段代码使用了 循环 ,逼格不够高。
对于一个整数而言,如果这个数是 4 的幂次方,那它必定也是 2 的幂次方。
我们先将 2 的幂次方列出来找一下其中哪些数是 4 的幂次方。
十进制二进制2104100 (1 在第 3 位)810001610000(1 在第 5 位)32100000641000000(1 在第 7 位)12810000000256100000000(1 在第 9 位)5121000000000102410000000000(1 在第 11 位)
找一下规律: 4 的幂次方的数的二进制表示 1 的位置都是在奇数位。
之前在小吴的文章中判断一个是是否是 2 的幂次方数使用的是位运算 n & ( n - 1 )。同样的,这里依旧可以使用位运算:将这个数与特殊的数做位运算。
这个特殊的数有如下特点:
- 足够大,但不能超过 32 位,即最大为 1111111111111111111111111111111( 31 个 1)
- 它的二进制表示中奇数位为 1 ,偶数位为 0
符合这两个条件的二进制数是:
1010101010101010101010101010101
如果用一个 4 的幂次方数和它做与运算,得到的还是 4 的幂次方数。
将这个二进制数转换成 16 进制表示:0x55555555 。有没有感觉逼格更高点。。。
代码实现
1 class Solution { 2 public boolean isPowerOfFour(int num) { 3 if (num <= 0) 4 return false; 5 //先判断是否是 2 的幂 6 if ((num & num - 1) != 0) 7 return false; 8 //如果与运算之后是本身则是 4 的幂 9 if ((num & 0x55555555) == num) 10 return true; 11 return false; 12 } 13 }
***************************第四道*******************************
题目描述
喜羊羊和灰太狼用几堆石子在做游戏。偶数堆石子排成一行,每堆都有正整数颗石子 piles[i] 。
游戏以谁手中的石子最多来决出胜负。石子的总数是奇数,所以没有平局。
喜羊羊和灰太狼轮流进行,喜羊羊先开始。 每回合,玩家从行的开始或结束处取走整堆石头。 这种情况一直持续到没有更多的石子堆为止,此时手中石子最多的玩家获胜。
假设喜羊羊和灰太狼都发挥出最佳水平,当喜羊羊赢得比赛时返回 true ,当灰太狼赢得比赛时返回 false 。
题目分析
举两个例子来帮助理解题意。
例子一:
输入:[ 5,3,4,5 ]
输出:true
解释:
喜羊羊先开始,只能拿前 5 颗或后 5 颗石子 。
假设他取了前 5 颗,这一行就变成了 [ 3 ,4,5 ] 。
如果灰太狼拿走前 3 颗,那么剩下的是 [ 4,5 ],喜羊羊拿走后 5 颗赢得 10 分。
如果灰太狼拿走后 5 颗,那么剩下的是 [ 3,4 ],喜羊羊拿走后 4 颗赢得 9 分。
这表明,取前 5 颗石子对喜羊羊来说是一个胜利的举动,所以我们返回 true 。
例子二:
输入:[ 5,10000,2,3 ]
输出:true
解释:
喜羊羊先开始,只能拿前 5 颗或后 3 颗石子 。
假设他取了后 3 颗,这一行就变成了 [ 5,10000,2 ]。
灰太狼肯定会在剩下的这一行中取走前 5 颗,这一行就变成了 [ 10000,2 ]。
然后喜羊羊取走前 10000 颗,总共赢得 10003 分,灰太狼赢得 7 分。
这表明,取后 3 颗石子对喜羊羊来说是一个胜利的举动,所以我们返回 true 。
这个例子表明,并不是需要每次都挑选最大的那堆石头。
题目回答
涉及到最优解的问题,那么肯定要去尝试一下使用 **动态规划 **来解决了。
先看一下力扣的正规题解:
让我们改变游戏规则,使得每当灰太狼得分时,都会从喜羊羊的分数中扣除。
令 dp(i, j) 为喜羊羊可以获得的最大分数,其中剩下的堆中的石子数是 piles[i], piles[i+1], ..., piles[j]。这在比分游戏中很自然:我们想知道游戏中每个位置的值。
我们可以根据 dp(i + 1,j) 和 dp(i,j-1) 来制定 dp(i,j) 的递归,我们可以使用动态编程以不重复这个递归中的工作。(该方法可以输出正确的答案,因为状态形成一个DAG(有向无环图)。)
当剩下的堆的石子数是 piles[i], piles[i+1], ..., piles[j] 时,轮到的玩家最多有 2 种行为。
可以通过比较 j-i和 N modulo 2 来找出轮到的人。
如果玩家是喜羊羊,那么它将取走 piles[i] 或 piles[j] 颗石子,增加它的分数。之后,总分为 piles[i] + dp(i+1, j) 或 piles[j] + dp(i, j-1);我们想要其中的最大可能得分。
如果玩家是灰太狼,那么它将取走 piles[i] 或 piles[j] 颗石子,减少喜羊羊这一数量的分数。之后,总分为 -piles[i] + dp(i+1, j) 或 -piles[j] + dp(i, j-1);我们想要其中的最小可能得分。
代码如下:
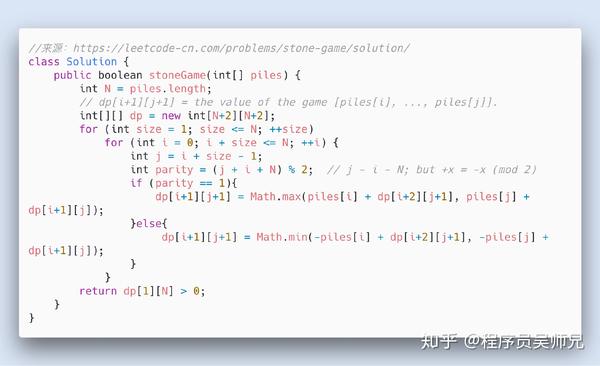
上面的代码并不算复杂,当然,如果你看不懂也没关系,不影响解决问题,请看下面的数学分析。
数学分析
因为石头的数量是奇数,因此只有两种结果,输或者赢。
喜羊羊先开始拿石头,随便拿!然后比较石头数量:
- 如果石头数量多于对手,赢了;
- 如果石头数量少于对手,自己拿石头的顺序和对手拿石头的顺序对调,还是赢。
所以代码如下:
1 class Solution { 2 public boolean stoneGame(int[] piles) { 3 return true; 4 } 5 }
看完之后,你的心情是怎么样的?
***第五道***
题目来源于 LeetCode 上第 172 号问题:阶乘后的零。题目难度为 Easy,目前通过率为 38.0% 。
题目描述
给定一个整数 n,返回 n! 结果尾数中零的数量。
示例 1:
输入: 3
输出: 0
解释: 3! = 6, 尾数中没有零。
示例 2:
输入: 5
输出: 1
解释: 5! = 120, 尾数中有 1 个零.
说明: 你算法的时间复杂度应为 O(log n) 。
题目解析
题目很好理解,数阶乘后的数字末尾有多少个零。
最简单粗暴的方法就是先乘完再说,然后一个一个数。
事实上,你在使用暴力破解法的过程中就能发现规律: 这 9 个数字中只有 2(它的倍数) 与 5 (它的倍数)相乘才有 0 出现。
所以,现在问题就变成了这个阶乘数中能配 多少对 2 与 5。
举个复杂点的例子:
10! = 【 2 *( 2 * 2 )* 5 *( 2 * 3 )*( 2 * 2 * 2 )*( 2 * 5)】
在 10!这个阶乘数中可以匹配两对 2 * 5 ,所以10!末尾有 2 个 0。
可以发现,一个数字进行拆分后 2 的个数肯定是大于 5 的个数的,所以能匹配多少对取决于 5 的个数。(好比现在男女比例悬殊,最多能有多少对异性情侣取决于女生的多少)。
那么问题又变成了 统计阶乘数里有多少个 5 这个因子。
需要注意的是,像 25,125 这样的不只含有一个 5 的数字的情况需要考虑进去。
比如 n = 15。那么在 15! 中 有 3 个 5 (来自其中的5, 10, 15), 所以计算 n/5 就可以 。
但是比如 n=25,依旧计算 n/5 ,可以得到 5 个5,分别来自其中的5, 10, 15, 20, 25,但是在 25 中其实是包含 2个 5 的,这一点需要注意。
所以除了计算 n/5 , 还要计算 n/5/5 , n/5/5/5 , n/5/5/5/5 , ..., n/5/5/5,,,/5直到商为0,然后求和即可。
代码实现
1 public class Solution { 2 public int trailingZeroes(int n) { 3 return n == 0 ? 0 : n / 5 + trailingZeroes(n / 5); 4 } 5 }
参考:程序员吴师兄 https://www.zhihu.com/question/33776070/answer/685253646 
