一、概念
1.定义与性质
(1)设x为二叉查找树中的一个结点,若y是x左子树中的一个结点,则key[y] <= key[x];若y是x右子树中的一个结点,则key[x]<=key[y]
(2)二叉查找树上执行的基本操作的时间与树的高度成正比。
2.结构
(1)结点结构:
关键字key
卫星数据data
分别指向父、左右孩子的指针p, left, right
3.在二叉查找树上的操作
查找一个关键字:SEARCH(x, k)
求最小关键字:MINIMUM(x)
求最大关键字:MAXIMUM(x)
求前驱:PREDECESSOR(x)
求后继:SUCCESSOR(x)
插入一个结点:INSERT(T, z)
删除一个结点:DELETE(z)
4.二叉查找树的应用
1.遍历:中序遍历、先序遍历、后序遍历
2.查找:查找包含某个关键字的结点,查找关键字最大或最小的结点、查找某个结点的前驱或后继
二、代码
1 #include <iostream> 2 #include <string> 3 using namespace std; 4 5 struct BST_Node 6 { 7 public: 8 int key;//关键字 9 int data;//卫星数据 10 BST_Node *left;//左孩子 11 BST_Node *right;//右孩子 12 BST_Node *p;//父结点 13 14 BST_Node(int x):key(x),data(x),left(NULL),right(NULL),p(NULL){} 15 }; 16 17 //二叉查找树的结构 18 class BST_Tree 19 { 20 public: 21 BST_Node *root; 22 BST_Tree():root(NULL){} 23 public: 24 //12.1 二叉查找树 25 void Inorder_Tree_Walk(BST_Node *x); 26 //12.2 查询二叉查找树 27 BST_Node *Tree_Search(BST_Node *x, int k); 28 BST_Node *Iterative_Tree_Search(BST_Node *x, int k); 29 BST_Node *Iterative_Tree_Minimum(BST_Node *x); 30 BST_Node *Iterative_Tree_Maximum(BST_Node *x); 31 BST_Node *Tree_Successor(BST_Node *x); 32 //12.3 插入和删除 33 void Iterative_Tree_Insert(BST_Node *z); 34 BST_Node *Tree_Delete(BST_Node *z); 35 }; 36 /*************12.1 二叉查找树****************************************************************/ 37 //递归的中序遍历 38 void BST_Tree::Inorder_Tree_Walk(BST_Node *x) 39 { 40 if(x != NULL) 41 { 42 //中序遍历当前结点的左子树 43 Inorder_Tree_Walk(x->left); 44 //访问当前结点 45 cout<<x->key<<endl; 46 //中序遍历当前结点的右子树 47 Inorder_Tree_Walk(x->right); 48 } 49 } 50 /********12.2 查询二叉查找树****************************************************************/ 51 //递归地查询二叉查找树 52 BST_Node *BST_Tree::Tree_Search(BST_Node *x, int k) 53 { 54 //找到叶子结点了还没找到,或当前结点是所查找的结点 55 if(x == NULL || k == x->key) 56 return x; 57 //所查找的结点位于当前结点的左子树 58 if(k < x->key) 59 return Tree_Search(x->left, k); 60 //所查找的结点位于当前结点的左子树 61 else 62 return Tree_Search(x->right, k); 63 } 64 //非递归的查询二叉查找树 65 BST_Node *BST_Tree::Iterative_Tree_Search(BST_Node *x, int k) 66 { 67 //不是叶子结点且不是所查找的结点 68 while(x != NULL && k != x->key) 69 { 70 //所查找的结点位于当前结点的左子树 71 if(k < x->key) 72 x = x->left; 73 //所查找的结点位于当前结点的右子树 74 else 75 x = x->right; 76 } 77 return x; 78 } 79 //非递归找最小值 80 BST_Node *BST_Tree::Iterative_Tree_Minimum(BST_Node *x) 81 { 82 //只要有比当前结点小的结点 83 while(x->left != NULL) 84 x = x->left; 85 return x; 86 } 87 //非递归找最大值 88 BST_Node *Iterative_Tree_Maximum(BST_Node *x) 89 { 90 //只要有比当前结点小的结点 91 while(x->right != NULL) 92 x = x->right; 93 return x; 94 } 95 //查找中序遍历下x结点的后继,后继是大于key[x]的最小的结点 96 BST_Node *BST_Tree::Tree_Successor(BST_Node *x) 97 { 98 //如果有右孩子 99 if(x->right != NULL) 100 //右子树中的最小值 101 return Iterative_Tree_Minimum(x->right); 102 //如果x的右子树为空且x有后继y,那么y是x的最低祖先结点,且y的左儿子也是 103 BST_Node *y = x->p; 104 while(y != NULL && x == y->right) 105 { 106 x = y; 107 y = y->p; 108 } 109 return y; 110 } 111 /*********12.3插入和删除**********************************************************/ 112 //二叉查找树的插入,非递归 113 void BST_Tree::Iterative_Tree_Insert(BST_Node *z) 114 { 115 //找到要插入的位置 116 BST_Node *x = root, *y = NULL; 117 //若x为空,x是要插入的位置,x的父是z->p 118 while(x != NULL) 119 { 120 y = x; 121 if(z->key == x->key) 122 { 123 cout<<"error:exist"<<endl; 124 return; 125 } 126 if(z->key < x->key) 127 x = x->left; 128 else 129 x = x->right; 130 } 131 //修改指针,注意树为空的情况 132 z->p = y; 133 if(y == NULL) 134 root = z; 135 else if(z->key < y->key) 136 y->left = z; 137 else y->right = z; 138 } 139 //二叉查找树的删除,实际删除的不一定是z,可能是z的后继 140 //然后把z的值改为实际删除结点的值 141 BST_Node *BST_Tree::Tree_Delete(BST_Node *z) 142 { 143 BST_Node *x, *y; 144 //若z最多只有一个孩子,实际删除的结点是z 145 if(z->left == NULL || z->right == NULL) 146 y = z; 147 //若z有两个孩子,实际删除的结点是z的后继 148 else 149 y = Tree_Successor(z); 150 //用x表示"实际要删除的结点"的孩子(最多一个孩子) 151 if(y->left != NULL) 152 x = y->left; 153 else 154 x = y->right; 155 //修改指针,以删去结点 156 if(x != NULL)//若"实际要删除的结点"没有孩子 157 x->p = y->p; 158 if(y->p == NULL)//若"实际要删除的结点"是根结点 159 root = x; 160 else if(y == y->p->left) 161 y->p->left = x; 162 else y->p->right = x; 163 //"若初阶要删除的结点"不是"待删除的结点",则内容替代 164 if(y != z) 165 { 166 z->key = y->key; 167 z->data = y->data; 168 } 169 return y; 170 }
三、练习
12.1 二叉查找树
12.1-2
二叉查找树:左子树关键字<根结点关键字<右子树关键字
堆:左子树关键字<根结点关键字 && 右子树关键字<根结点关键字
不能,因为一个结点的的左子树与右子树的关键字大小没有关系
12.1-3
用栈实现:见算法导论-10.4-有根树的表示中的10.4-3
不用栈实现:见算法导论-10.4-5
12.1-4
1 //递归的先序遍历 2 void BST_Tree::Preorder_Tree_Walk(BST_Node *x) 3 { 4 //x不是叶子结点 5 if(x != NULL) 6 { 7 //访问当前结点 8 cout<<x->key<<' '; 9 //先序遍历当前结点的左子树 10 Preorder_Tree_Walk(x->left); 11 //先序遍历当前结点的右子树 12 Preorder_Tree_Walk(x->right); 13 } 14 } 15 //递归的后序遍历 16 void BST_Tree::Postorder_Tree_Walk(BST_Node *x) 17 { 18 //x不是叶子结点 19 if(x != NULL) 20 { 21 //后序遍历当前结点的左子树 22 Postorder_Tree_Walk(x->left); 23 //后序遍历当前结点的右子树 24 Postorder_Tree_Walk(x->right); 25 //访问当前结点 26 cout<<x->data<<' '; 27 } 28 }
1 12.2-1 2 c,e 3 12.2-2 4 //递归地查找最小值 5 BST_Node *BST_Tree::Tree_Minimum(BST_Node *x) 6 { 7 if(x->left != NULL) 8 return Tree_Minimum(x->left); 9 else return x; 10 } 11 //递归的查找最大值 12 BST_Node *BST_Tree::Tree_Maximum(BST_Node *x) 13 { 14 if(x->right != NULL) 15 return Tree_Maximum(x->right); 16 else return x; 17 } 18 12.2-3 19 //查找中序遍历下x的前驱,即小于x的最大值 20 BST_Node *BST_Tree::Tree_Predecessor(BST_Node *x) 21 { 22 //如果x的左子树非空 23 if(x->left != NULL) 24 //x的前驱是x的左子树的最大值 25 return Tree_Maximum(x->left); 26 //如果x的左子树为空且x有前驱y,那么y是x的最低祖先结点,且y的右儿子也是 27 BST_Node *y = x->p; 28 while(y != NULL && x == y->left) 29 { 30 x = y; 31 y = y->p; 32 } 33 return y; 34 } 35 12.2-4 36 (1) 37 4->left = 2 4->right =NIL 38 2->left = 1 2->right = 3 39 搜索路径4-2-1 40 (2) 41 1->right = 3 1->left = NUL 42 3->left = 2 3->right = 4 43 搜索路径1-3-4
12.3 插入和删除
12.3-1
1 //递归的二叉查找树的插入操作,分三种情况 2 void BST_Tree::Tree_Insert(BST_Node *x, BST_Node *z) 3 { 4 //已经存在 5 if(z->key == x->key) 6 { 7 cout<<"error:exist"<<endl; 8 return; 9 } 10 //插入到x的左子树中 11 else if(z->key < x->key) 12 { 13 //x没有左子树 14 if(x->left == NULL) 15 { 16 //修改指针,插入操作 17 x->left = z; 18 z->p = x; 19 return; 20 } 21 //x有左子树 22 else 23 //对x的左子树执行插入操作 24 Tree_Insert(x->left, z); 25 } 26 //插入到x的右子树中,与上面类似 27 else if(z->key > x->key) 28 { 29 if(x->right == NULL) 30 { 31 x->right = z; 32 z->p = x; 33 } 34 else 35 Tree_Insert(x->right, z); 36 } 37 }
12.3-3
最坏是n^2
最好是nlgn
12.3-4
求y的前驱z分为两种情况,以下分别讨论:
(1)y有左孩子,则z是left[y]中最右边的结点,z没有右孩子,因此删除z时直接删除修改指针即可,没有问题
(2)y没有左孩子,则z是y的祖先,y是z右子树是最左边的点,又分为两种情况:
(2.1)若z没有左孩子,则直接删除z并修改指针,没有问题。
(2.2)若z有左孩子,则不直接删除z,而是用z代替y存在并删除y。这里会有问题,另一个数据结构中的保存了指向y的指针,但是y的内容转移到另一个结点上了,指向y的指针指向了一个被释放的空间。
解决方法:使TREE-DELETE返回删除后的y的指针,这个值可能会变,可能不变。让另一个数据结构的y指针指向TREE-DELETE的返回值。
12.3-5
不或交换,反例如图
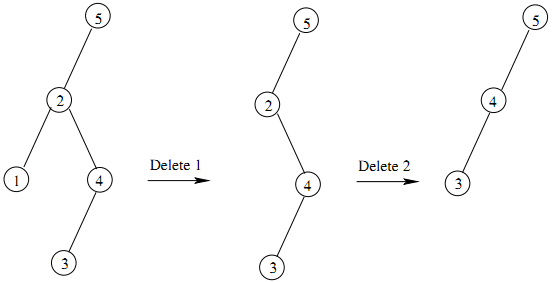
12.3-6
当待删除结点有两个子树时,不删除待删除结点,而是删除它的前驱或后继,用随机数rand()%2来确定删除的前驱还是后继
代码见文:二
四、思考题
12-1 具有相同关键字元素的二叉树
12-2 基数树
12-3 随机构造的二叉查找树中的平均结点深度
f)待解决