精读45-180程序转弯模板
大家好,我是画螺旋画的停不下来的刘崇军。今天和大家分享一下45-180程序转弯模板的计算过程。
简要说明一下,风螺旋精确计算方法是对传统的分段圆弧画法的一种数学实现,它们之间是精确替代关系。风螺旋计算的关注点是:风螺旋的初始参数(rotation、offset、圆心点位置)和结束参数(通常为公切线的角度)。风螺旋起点到终点之间的部分通过使用风螺旋公式自动化计算而来,在分析时不单独说明。
先来了解一下45-180程序转弯模板的飞行方法:
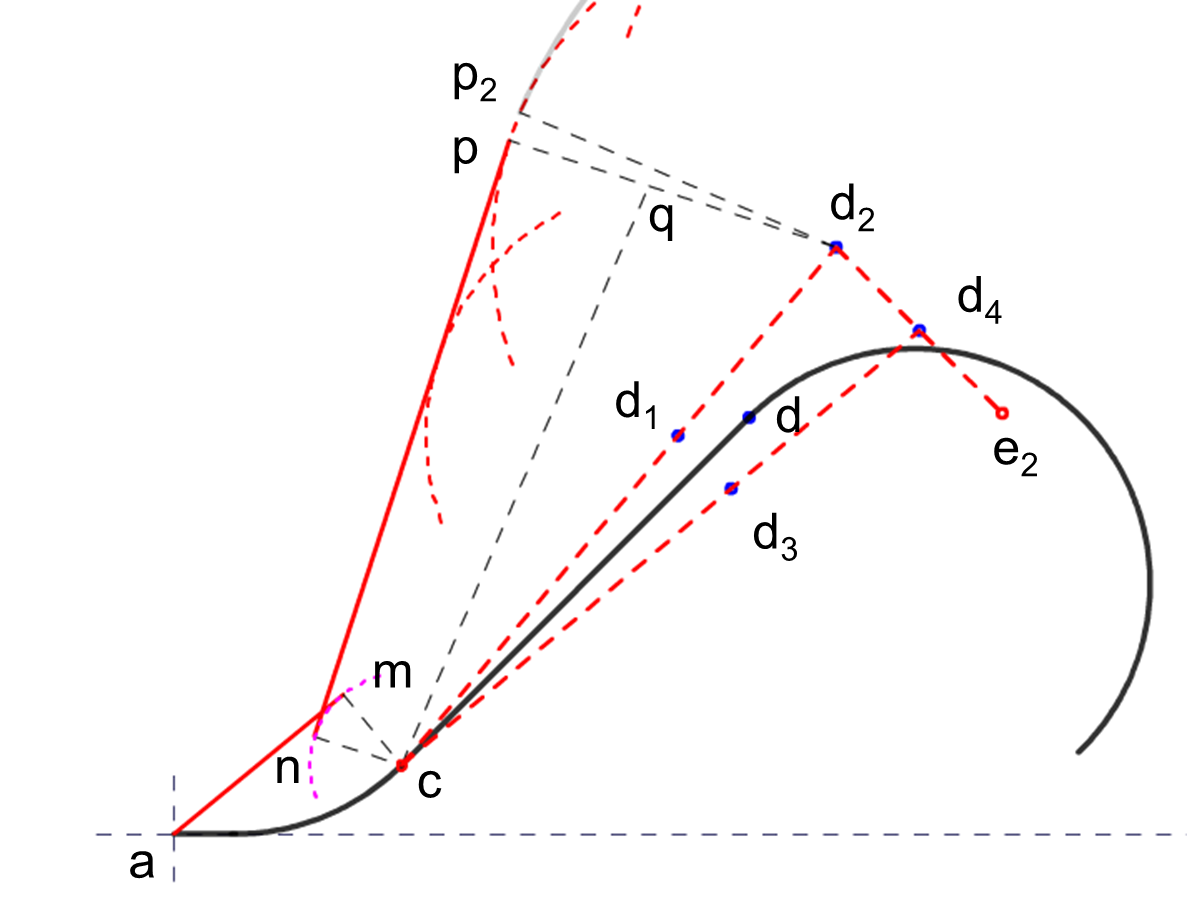
图1 标称航迹与模板初始段位置关系
航空器从 a 点开始经过5“(建立坡度时间)直飞到达b点,从b点开始向航迹一侧转弯45°(图1中为左转),之后直线飞行一段时间到达d点(从a 点 到 d 点的总飞行时间为:AB类1分钟,CD类1.25分钟)。过d点后向另一侧转弯180°(图1中为右转),切入向台航迹,飞向导航台。
直线飞行段需要考虑 5° 的航迹保持误差,因此,从 c 点开始在航迹两侧各画 5° 线,表示可能存在的标称航迹。d 点是完全排除了一切误差的标称点,按照航迹误差、计时的长短(此处不是计时误差),得到 d 点的”容差点“: d1 d2 d3 d4,这四个点就是风螺旋计算的起点。
d 点的距离计算方法是:直线段(ab = 5v) 加上 转弯45° 的距离,再加上 直线段(cd = (t-5-45/R)*v )计算得到。从 cd 的计算公式可知,t 代表的是从a点至d 点的总飞行时间,包含了ab段的 5秒直线飞行,与转弯45°所消耗的时间,因此,若称之为”出航时间“是不合适的。
d 点的最早容差点 d1 d3 的计算方法是在 d 点计算的基础上,减少了 5秒的坡度恢复时间。45°转弯结束时需要5”来进行姿态恢复,d 点的计时中已包含了这部分距离,在计算最早点时,需将这 5 秒减去 (个人观点,仅供参考),因此 cd1=cd2 = cd-5v 。
d 点的最晚容差点 d2 d4 的计算方法是在 d 点计算的基础上,增加了 进入180°转弯前的5秒的坡度建立时间,再加上10秒的计时误差,总计 15"时间。因此 cd2 = cd4 = cd + 15v 。
最早、最晚点之间相差20秒时间,这个数字很重要,后面计算风螺旋公切线时会用到。
图1中显示了45°转弯外边界的切线位置。从图中可以看到,c 点圆弧的半径为 5“的风速,加上45°转弯过程累积的风速距离(45E,E表示每转弯一度所产生的风偏移量),即 Wc = 5w + 45E。
d2点处的圆弧半径,等于从c点开始,先飞到d 点再飞15秒才能到达的位置,从a 点飞至 d 点,需要 t 秒,总共的风影响量(圆弧半径)为 Wd2= (t + 15)*w。
知道了 c 与 d2 处的圆弧半径,可以得到切线 np 与 cd2 之间的夹角:arcSin( ( Wd2- Wc)/ cd2 = arcSin( (t+15)*w '-(5w '+45E) )/cd2。
由于 E=w '/R ,上式可化简为 arcSin( (t+10w '-45/R)*w ' )/ cd2)。将cd2 = (t -5 +45/R + 15)*v ,代入,可知∠ qcd 2 = arcsin(qd 2/cd 2) = arcsin(w '/v) = DA ,即公切线 np 与 cd 2的夹角 为最大偏流的夹角DA。
偏流角DA在风螺旋的计算中随处可见,直线段夹角也等于DA,其实并不偶然,因为,偏流角最初的定义就是直线飞行时受偏流的影响而形成的最大外扩角度。
刚刚简单证明了一下直线段的切线与标称航迹夹角为DA,这里隐藏了另外一个问题,那就是图2中 d2p2 线与 e2d2 沿长线的夹角也等于DA(风螺旋Esita外扩方向),因此,在 d2p 与 d2p2 之间就存在了一个夹角,这个夹角正好等于5°,整个模板在这个位置仿佛被撕开了一个口子,这种情况在后面的基线模板、等待模板中都普遍存在。这个5°夹角产生的原因,是传统模板中风螺旋起点的半径是按照与标称航迹相垂直,而不是与5°偏航容差线相垂直而造成的,因此,5°偏航容差在外边界的衔接中就体现为 5°的缝隙。在现阶段5°的缝隙可以直接以同一个半径相连接,但对于计算机处理而言它有着不同的含意。
过去的模板分析中并未有5°缝隙的相关讨论,主要原因分段圆弧画法的模板精度是有欠缺的。当采用风螺旋计算时,相当于高清画质的情况下,每一度的计算都可以找到相应的依据,因此,对于类似这样”缝隙“的存在,是清晰可见的。
PBN模板计算时,通常风螺旋是从主区开始绘制,转弯半径与标称航迹”天然“的垂直,没有 5° 航迹误差的存在,因此,”恰好“没有了这种在传统模板中非常常见的5°缝隙。从这个角度来说,PBN模板真得是非常适合计算机的自动化处理,未来我们会讨论到这个话题。
d 点的容差点就是风螺旋的起点(这里的起点指的是含有初始外扩距离的风螺旋的计算起点,和通常所说的螺旋线从这一点开始绘制 不是相同的概念),因此很容易的想到,45-180程序转弯模板中应该有4条风螺旋,但实际的模板中只用到了其中的3条。三条风螺旋的位置关系如下图所示(图中蓝色曲线为风螺旋线):

图2 45-180程序转弯模板中的风螺旋
d1点为起点的风螺旋在d3之内,仅在切入向台航迹时才会有所体现,因此,在ICAO8168里被直接拿掉了(同情一下 -。-!)。现在只有3条风螺旋了,我们以风螺旋的圆心点来命名风螺旋,则分别有 e2 e3 e4 三条风螺旋。
用来绘制圆弧的对应点按这3条风螺旋来分类,将是这样的:
e2 系列 d2 f g
e4 系列 d4 h i j
e3 系列 d3 k l (这几个点之间离得有点远,正常情况下是按50度间隔)
每个系列中的对应点,都是按照该系列的起点,加上转弯角度所换算出的风偏移量进行计算的。当你对各个点的计算存在疑问时,最好先了解一下它属于哪个系列的风螺旋,检查一下初始点的外扩距离是多少,再进行转弯过程的数值累积计算,通常可以得到一个较好的验证结果。
各个点的数值大小不是风螺旋的关注重点,所以全部略过,接下来分析一下公切点的位置计算。
e2 风螺旋与 e4 风螺旋初始角度相同,初始外扩距离相同,根据公切线的计算方法:公切线 与 圆心点连线 的 夹角 = arcSin((Esita2-Esita1)/Distance),外扩距离相等的情况下,夹角等于零,即公共线与 e2 e4之间的连线相平行。根据风螺旋原理,切线角度为90度时,对应的sita 角度为 90+DA。因此,e2风螺旋的终点角度为 90+DA,e4 风螺旋的(绘制)起点角度为 90+DA。(对于离场转弯等绘制相同参数的两条风螺旋的情况下,这个计算方法同样适用)
第一组公切线的位置如图3所示(可以口算出来的切点位置,不算很难吧?:-)
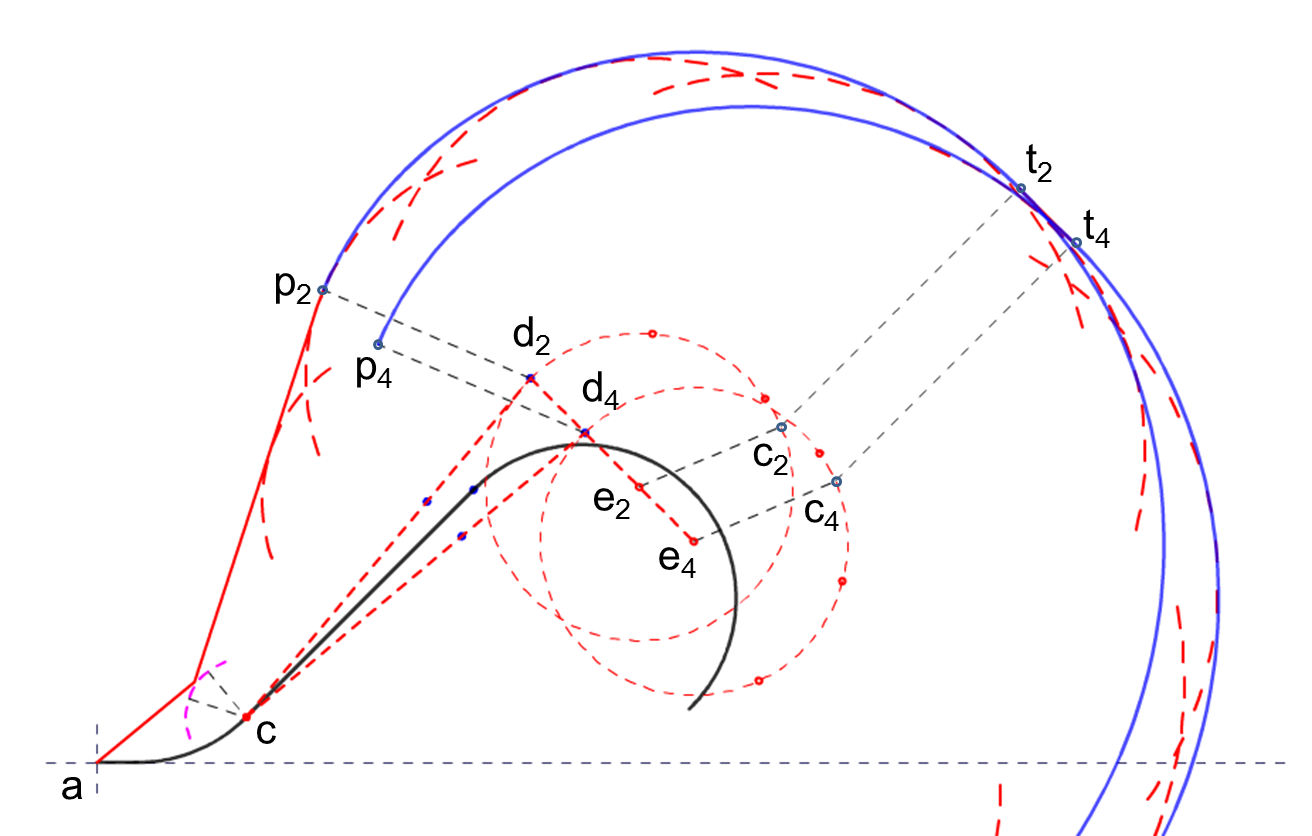
图3 90°+DA所确定的公切线位置
e4 e3 风螺旋的公切线计算稍微复杂一点点,按照标准步骤推演一下:
1、确定初始旋转角度(rotation,以软件系统中水平向右为起点,顺时针角度增加来计算)
e4风螺旋 rotation4 = 225°
e3风螺旋 rotation3 = 225°
2、确定初始外扩距离(offset)
e4风螺旋 offset4 = Wd4 = (t+15)w = 2.25km
e3风螺旋 offset3 = Wd3 = (t -5)w = 1.64km
3、计算圆心点的连线距离与角度
e3 e4之间的距离 distance = cd4 - cd3 = 20v = 1.62km
e3 e4之间的角度 angle = -45 + 5 +180 = 140°
4、计算公切与圆心连线之间的夹角
alpha = arcSin( (offset4 - offset3 -(rotation3-rotaion4)*E )/ distance)
将前面的代数式代入之后,有趣的一幕发生了,
alpha = arcSin((( t+15)w - (t-5)w ) / 20v ) = arcSin( 20w / 20v) = DA
我们刚刚似乎在历史上首次证明了,45-180模板中e3 e4 风螺旋的切线 与 圆心点的连线 之间的夹角为偏流角(惊不惊喜,意不意外?)。
冷静、冷静一下,这个结果其实并不意外。假如飞机是从 e3 点飞向 e4 点,这属于直线飞行,外扩角当然是 DA 角,将 e3 e4 直线段飞行所积累的风偏移量原样搬移到转弯180°之后,偏移量与距离的比仍然会保持相同的计算结果(图4中的c5c6段),所以,这里的计算只是进一步证明了这个结论,切线的位置点如图4所示。
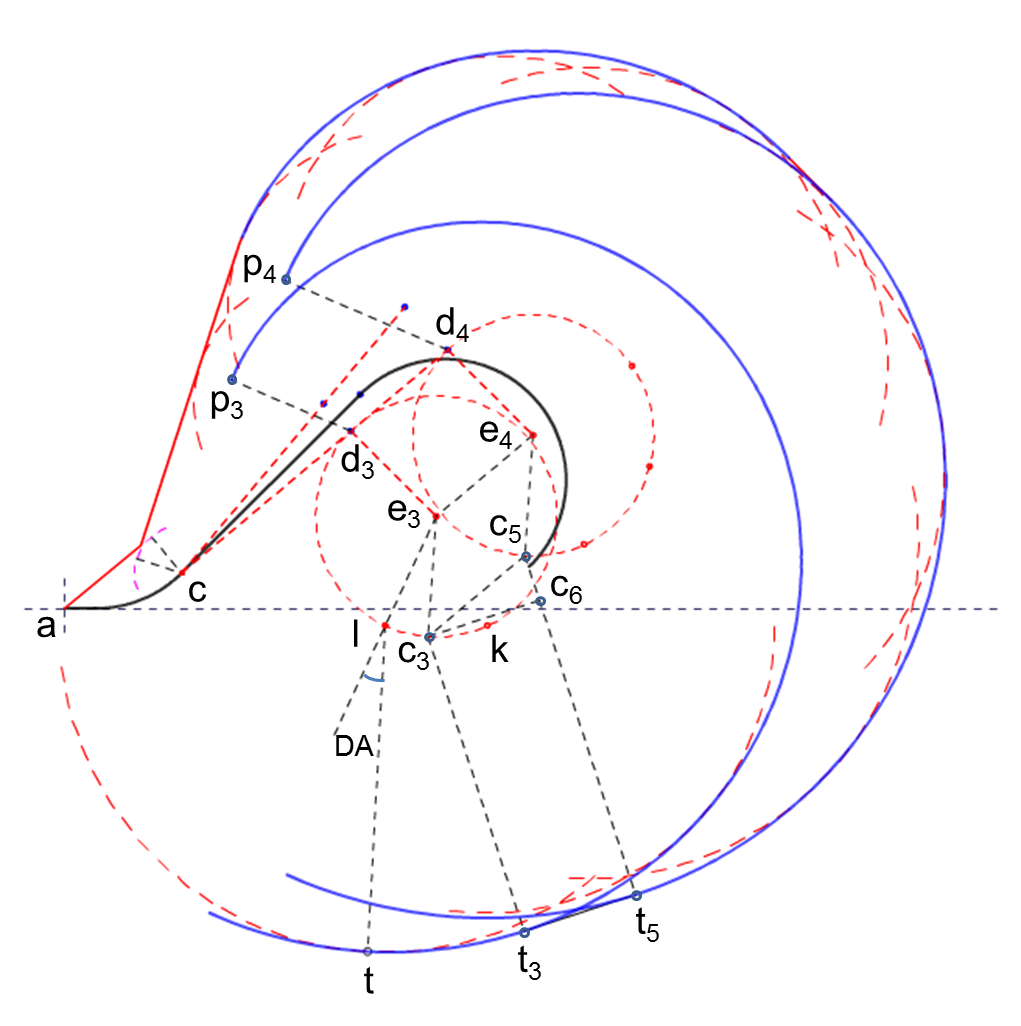
图4 e4 e3风螺旋公切线位置关系
5、计算公切线两端的螺旋的角度
公切线角度知道、圆心点连线角也知道的情况下,接下来就可以根据风螺旋原理(一个神秘的原理)口算sita 角度。
e4风螺旋的结束角度:
sita4 = (140°+360°)+DA - 90° + DA - 225 = 2 DA + 185°
e3风螺旋的结束角度:
sita4 = (140°+360°)+DA - 90° + DA - 225 = 2 DA + 185°
在标准模板中 DA 角的计算值为21.9°,因此,e3风螺旋的绘图起点为2*21.9° + 185° =229°,是比 Wk 点略晚一点的位置,Wk 代表了转弯200°时的位置。
e3、e4风螺旋的初始旋转角度相同,公切线位置所对应的转弯角度 sita 值也是相同的,所产生的外扩距离的差异来自于初始外扩距离的不同,即初始外扩距离中相差了 20秒的风速,这是决定它们的公切角度的决定因素。
ICAO最终的模板省略了很多的技术细节,如下图所示:

ICAO标准模板中采用的是 L 点(250°转弯)的外扩圆弧,向 a 点做切线形成的封闭模板。通过风螺旋线的走向分析 及 对照 9371文件( Template manual for holding reversal and racetrack procedures),可以知道这样的作法没有必要。模板不能等同于保护区,a 点在实际应用时,应根据定位容差去”摆放“,形成的最大范围才是保护区。
从算法研究来说,实现模板的自动化计算,已经是达成了预期目标。后续实现保护区的过程中,实际上是要根据模板的思路将模板”打散“,将风螺旋放置于不同的定位容差点,自动化的计算出最外侧的公切线,与风螺旋相衔接成为完整的保护区。
相关文章阅读:
题外话:
今天的配图是彩色的,上一篇文章《80-260模板》大部分配图是纯黑白的,它们的区别是:彩色配图是之前写论文时用 Flash 编程实现的图片(Flash 的绘图系统真的是很完美),黑白色配图是近期学习 C# 之后,代码搬迁之后的成果。初学 C#, 很多东西没消化,所以暂时顾不上解决色彩问题了(求 C# 高手指导一下)。
与本篇文章相关的论文发表于2017年4月的《航空计算技术》,论文的引用格式为:
[1] 刘崇军, 赵航. 风螺旋线精确算法在程序转弯模板中的应用[J]. 航空计算技术, 2017, 47(3):62-65.