在飞行程序设计中,偏流角(Draft Angle简写为DA)通常指得是受侧风影响航向偏移的最大角度。用速度向量来表示时,是图1中的三角形关系:

图1中假定风速度向量(w)的方向是可变的,则风速度向量的范围是一个圆周,当地速度向量(GS)与风速度向量相垂直时,DA角最大。
在直线运动中,速度向量乘以时间,得到距离,距离的比值关系仍然符合这个关系,如图2所示:

将速度的比例关系放到圆周运动中来观察,与特定的风速w相关的最大偏流角DA的位置关系如图3所示:

图3中,线段c1c与真空速向量(v)相垂直,因此,线段c1c与线段c2c之间的夹角等于DA角,用数值来表示DA= arcsin(w/v)。
根据等距螺旋的原理,螺旋线是直线运动与圆周运动的叠加,风螺旋是等距螺旋的一种特殊形式。以风速向量最大外扩方向做为直线运动的方向,将这个直线向内进行延长,可以得到图4中的效果。

根据对顶角的关系,图4中所标注的橙色线,与标称圆半径的夹角均为DA角,若增加直线的绘制“密度”,可以得到图4中所示的红色圆。红色圆的半径用D来表示,则它的值等于D=r*sin(DA)。
由于风螺旋中的sin(DA)又等于w/v,因此,w/v 就等于D/r,二者均为DA角的 正弦值。
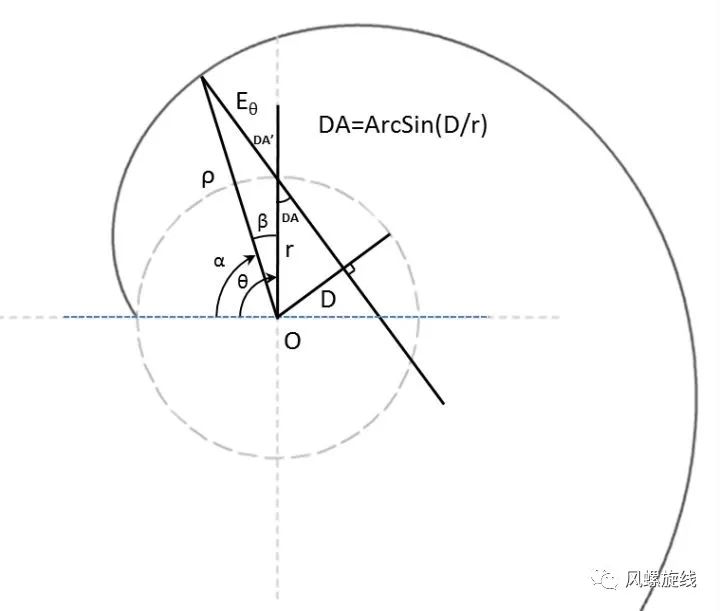
回到等距螺旋的话题中来,直线与圆周相交,直线与圆心点的最近距离为D(中文发音:大地)。从圆心向直线做垂线,垂点可称为近地点,是直线轨迹与圆心最接近的一个位置点。
令D的取值范围为0到r(圆周半径),当D为零时,直线运动与圆周运动叠加可以产生阿基米德螺旋;当D不为零,且速度比等于D/r时,可以得到风螺旋线;当D等于r,且速度比为1时,可以得到渐开线(风螺旋与渐开线对于旋转方向有一定要求,这里暂不详述)。更多的位置随意、速度比任意的螺旋,可以统称为自由螺旋。等距螺旋的分类大致就是这样。
DA角在等距螺旋中可以当做是D边所对应的角度,正如图5所示,所以它在等距螺旋中也可以理解为D-Angle(D角)。等距螺旋是从风螺旋扩展而来,很多的概念沿用了风螺旋的概念,随着等距螺旋概念的不断普及和深化,风螺旋将不再神秘,飞行程序设计自动化的浪潮也即将袭来。
往期文章回顾
两年前发现的结论,今年才将等到正式论文的刊发,这才是真实的科研节奏,汗一个。
风螺旋线从今天起正式升级为等距螺线!(2016-5-4)
等距螺旋的并不是一个全新的名词,只是我们重新定义了它,并且通过它将阿基米德螺旋、风螺旋、渐开线螺旋 画上了等号。
等距螺旋的概念非常烧脑,所以在公式推导之前,一定是先对原理进行反复的说明。或许当下理解这个概念还比较困难,这其实很正常,不必因此而感到挫折。
为 什么螺旋线的概念一直没有太大的变化呢?即使很多人都发现,阿基米德螺旋与渐开线是如此的“相似”,却无法在这二者间建立一个统一的公式。我想根本的原因还是因为“无用”两个字,即使电脑动画可以明白无误的画出很多种的螺旋,但因为这些螺旋的确没有太大用处,所以,少有人去分析它们的关系。而风螺旋计算是飞行程序设计中必须解决的一个问题,因此,才产生了“有用”的价值。所以,等距螺旋的产生条件中,风螺旋是一个必有的条件,而这个机遇恰好被我捡到了,仅此而已。