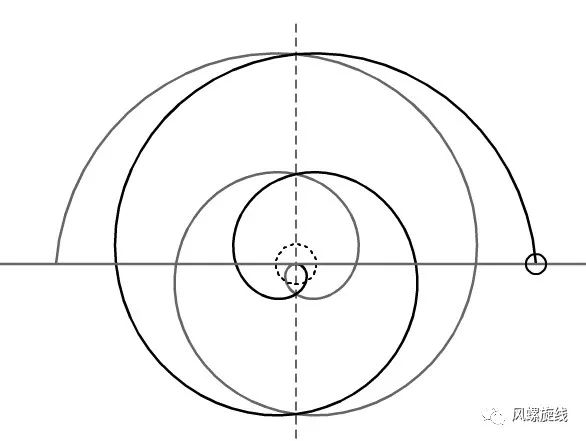
阿基米德螺旋、渐开线螺旋、风螺旋是等距螺旋的典型特例,它们的计算公式可以统一用等距螺旋公式来表示。
等距螺旋的理论基础是圆周运动与直线运动的叠加,它的形态与运动的方向、速度的大小有密切的关系。
假定圆周运动的速度为v,直线运动的速度为w,二者构成的等距螺旋的极坐标公式有下面三个:
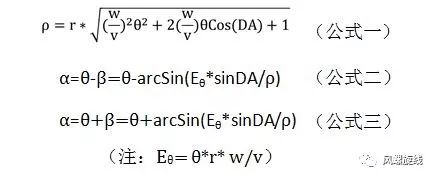
图1 等距螺旋的基础公式
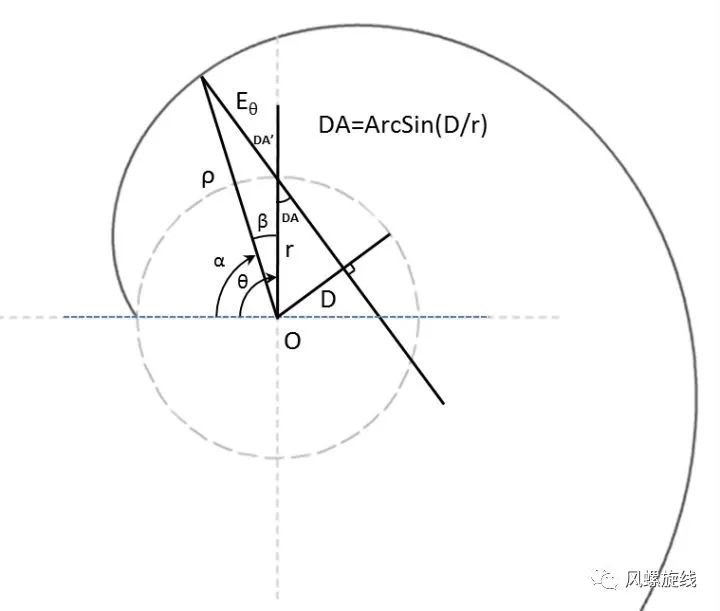
图2 等距螺旋角度关系图
若公式二的螺旋是顺时针外扩的,则公式三表示的是逆时针外扩的螺旋。
(先来热个身,插一段题外话)
等距螺旋公式与圆周公式的关系
当直线运动的速度w=0时,将得到ρ=r和α=θ,这刚好是圆的极坐标公式。也就是说,在没有外部因素的干扰下,可以将圆看成为圆周运动的轨迹。
这里还体现了等距螺旋公式的一个特点,那就是,等距螺旋公式中角度的起点是从直线与圆周相交的那点开始计算的。而以往的螺旋公式通常是从圆心点(阿基米德螺旋)、或近地点开始(渐开线)开始计算角度。
等距螺旋公式与阿基米德螺旋公式的关系
根据等距螺旋中直线与圆的位置关系,阿基米德螺旋的直线运动是穿过圆心的,因此,DA角的值为零。
代入等距螺旋公式可得:
ρ = r*((w/v)*θ+1) 或表示为ρ = (r*w/v)(θ + v/w)
α=θ
常见的阿基米德螺旋公式为ρ = a θ + b或者ρ = a θ。
对比等距螺旋生成的公式可以发现,常用的阿基米德螺旋公式中忽略了太多的参数细节,直接导致了对阿基米德螺旋中速度认知的偏差。
具体来看,等距螺旋θ值为零时,ρ = r,代表的是圆周上的一点。若用ρ = a θ来计算螺旋,θ值为零时,代表的是圆心点。两个θ之间相差v/w弧度单位。
图3 风螺旋等距外扩的示例(与本文内容无关)
常用公式中的系数a,在等距螺旋中代表了r*w/v,即半径乘以直线运动的速度除以圆周运动的速度。半径的大小隐藏在了系数a中,绝大多数情况下,阿基米德螺旋中都没有提及到特定的半径。
若指定了较大的半径,对于相同的系数a,相当于圆周运动速度v增加,而直线运动速度w减小,其计算结果是相同的。因此,在阿基米德螺旋中并不关心半径倒底有多大,但半径一定是不为零的。
根据等距螺旋公式可以看到,直线运动与圆周运动的速度并不单独出现在公式中,而是以速度比的方式出现。也就是说,对于指定的半径,不同的阿基米德螺旋之间的区别实际上是速度比不同而已。

图4 风螺旋等距外扩示例(与本文内容无关)
举个例子,如果旋转的速度增大一倍,则旋转周期T将缩小一倍,此时,若直线运动的速度也增大一倍,那么在一个旋转周期结束时,圆周会回到原来的位置上,而直线上运动了相同的距离,得到的是将同样的螺旋线轨迹。
等速螺旋的定义中将速度限定为匀速,忽视了速度比的存在。因而等速螺旋无法解释,在速度同时倍增时,螺旋保持不变这一情况。
等速度比才是等距螺旋更深层的特质。

微信扫一扫
关注该公众号