codeforces 486B.OR in Matrix 解题报告

题目链接：http://codeforces.com/problemset/problem/486/B

题目意思：给出一个m行n列的矩阵B(每个元素只由0/1组成)，问是否可以利用矩阵B，通过一定的运算逆回来求出矩阵A（行和列数都跟B相同）。可以的话输出"YES" 并输出矩阵A，否则输出 "NO"。运算如下：

    

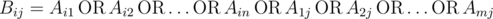
     也就是，Bij 是通过 A 矩阵第 i 行中所有的数做 或（|） 运算接着再跟所有第 j 列中所有的数做 或 运算求出来的。or 运算就是除了所有元素都为 0 的情况，or出来的结果为0外，其他情况算出来都是1（至少有一个元素是 1 即可）。

    以下注释部分可以忽略～～～

    /******************************************

     我一开始的错误做法是利用两个数组 row[] 和 col[] ，初始化使得row[1]～row[m] 都为1，col[1]～col[n] 都为1。当 Bij = 0 时，令 row[i] = 0，col[j] = 0来表示第 i 行 和 第 j 列都必须要填 0。这样才能保证 or 出来的结果是0嘛～～然后找出矛盾，即如果b[i][j] = 0，它需要满足row[i] == 0 且 col[j] == 0；如果b[i][j] = 1，但遇到row[i] == 0 且 col[j] == 0，那么就表示有矛盾啦。最后就根据如果row[i] == 0 或者 col[j] == 0 就输出0，否则输出1。

    不过仔细想一下，其实填1的情况是比较复杂的，例如b[i][j] = 1，那么并不能确定究竟是因为row[i] = 1 还是 col [j] = 1，而输出如果仅仅是根据 row[i] == 0 或者 col[j] == 0 输出0是不对的，试想，因为只要保证其中一个（row[i] == 0 && col[j] == 1类似这种）是1即有可能输出1了。于是最终测试遇到这组数据的时候就呵呵了～～～（我的输出是9个0，明显是错的）

     1  0 0

     1  0 0     

　   1  0 0

   如果按我的做法，那么分析结果是row[1] = 0, row[2] = 0, row[3] = 0，col[1] = 1，col[2] = 0，col[3] = 0。b[i][j] == 1 且 row[i] == 0 && col[j] == 0 是得不出矛盾的。例如b[1][1] = 1，它只是row[1] = 0，但col[1] != 0。

************************************************/

    正确的做法要用到逆向思维。首先根据b[i][j]构造出相应的a[i][j] 哪些数必定为1。如果b[i][j] = 0，那么a[i][0]～a[i][n-1] 都为0，a[0][j]～a[m-1][j] 都为0。那么逆回来就是如果a[i][j] = 1，那么b[i][0]～b[i][n-1]所有元素都为1，b[0][j] ～b[m-1][j]所有元素都为1，就是没有一个元素等于0！是不是很神奇呢～～～～然后利用矩阵a求出对应的b'[i][j]（代码中是c[i][j]），然后对比b[i][j]是否跟c[i][j]不同，不同即引出矛盾。

      这种思维确实需要好好锻炼!!!

#include <iostream>
#include <cstdio>
#include <cstdlib>
#include <cstring>
using namespace std;

const int maxn = 100 + 10;
int a[maxn][maxn], b[maxn][maxn];
int c[maxn][maxn];

int main()
{
    int m, n;
    while (scanf("%d%d", &m, &n) != EOF)
    {
        for (int i = 0; i < m; i++)
        {
            for (int j = 0; j < n; j++)
                scanf("%d", &b[i][j]);
        }
        memset(a, 0, sizeof(a));
        for (int i = 0; i < m; i++)   // 构造a矩阵
        {
            for (int j = 0; j < n; j++)
            {
                bool ok = false;
                for (int l = 0; l < m; l++)  // 行
                {
                    if (!b[l][j])          
                        ok = true;
                }
                for (int l = 0; l < n; l++)  // 列
                {
                    if (!b[i][l])
                        ok = true;
                }
                if (!ok)          // a[i][j] 填1必须要满足b[0][j]～b[m-1][j]以及b[i][0]～b[i][n-1]没有一个元素等于0。
                    a[i][j] = 1;
            }
        }
        // 从a矩阵经计算应该得到的b矩阵
        for (int i = 0; i < m; i++)
        {
            for (int j = 0; j < n; j++)
            {
                if (a[i][j] == 1)
                {
                    for (int l = 0; l < m; l++)
                        c[l][j] = 1;
                    for (int l = 0; l < n; l++)
                        c[i][l] = 1;
                }
            }
        }
        // 检查是否有矛盾
        bool ok = true;
        for (int i = 0; i < m && ok; i++)
        {
            for (int j = 0; j < n && ok; j++)
            {
                if (c[i][j] != b[i][j])
                {
                    ok = false;
                    break;
                }
            }
        }
        printf("%s
", ok ? "YES" : "NO");
        for (int i = 0; i < m && ok; i++)
        {
            for (int j = 0; j < n; j++)
                cout << a[i][j] << (j == n-1 ?  "
" : " ");
        }
    }
    return 0;
}