题目链接:http://codeforces.com/problemset/problem/501/C
题目意思:有 n 个点,编号为 0 ~ n-1。给出 n 个点的度数(即有多少个点跟它有边相连)以及跟它相连的点的编号的异或结果。最后需要输出整幅图的所有边的情况。
这道题确实是一道很好的题目!!!!它说拓扑排序的变形,需要队列的运用,还有就是异或计算的性质!!!(非一般厉害)
由于是无向无环的简单图,换言之就是一棵树啦^_^。那么它就肯定有叶子结点,叶子节点的度数为1,此时它相邻点的异或结果实际上就是所求点的编号了。然后把跟叶子节点相邻的点的度数-1,代表把叶子节点去除,此时异或结果是有变的。需要用本来的异或结果跟该叶子节点再异或一次,就得出除了这个叶子节点外其他点的异或值了。举个例子吧,假如有一幅图是这样的。
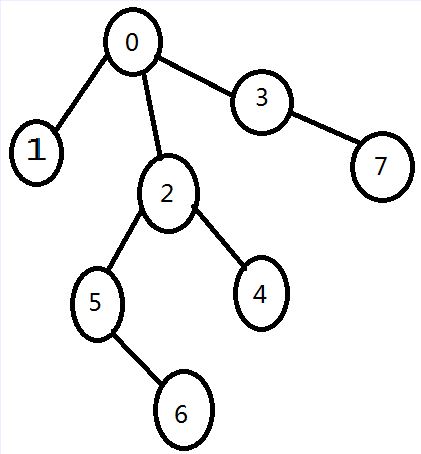
0 的相邻点有1、 2、 3,异或出来的结果是0,它的度数是3.那么当处理0-1这条边时,容易知道去除1这个点后,只有2和3异或了:10 ^ 11 = 1,刚好等于 1 ^ 2 ^ 3 ^ 1 (01 ^ 10 ^ 11 ^ 01)。异或的一个性质就是a^b^c^a = b ^ c。是不是很神奇呢~~~~当然我们总是处理那些度数为1的点,把这些点放入队列里面,依次处理。
1 #include <iostream> 2 #include <cstdio> 3 #include <cstdlib> 4 #include <queue> 5 using namespace std; 6 7 #define f first 8 #define s second 9 10 const int maxn = (1<<16) + 5; 11 int degree[maxn], XOR_sum[maxn]; 12 13 int main() 14 { 15 #ifndef ONLINE_JUDGE 16 freopen("in.txt", "r", stdin); 17 #endif // ONLINE_JUDGE 18 19 int n; 20 while (scanf("%d", &n) != EOF) { 21 queue<int> q; 22 pair<int, int> ans[maxn]; 23 for (int i = 0; i < n; i++) { 24 scanf("%d%d", °ree[i], &XOR_sum[i]); 25 if (degree[i] == 1) 26 q.push(i); 27 } 28 int cnt = 0; 29 while (!q.empty()) { 30 int from = q.front(); 31 q.pop(); 32 if (degree[from] == 1) { // 这句判断很重要,因为有可能degree[]--过程中使得变为0 33 int to = XOR_sum[from]; 34 ans[cnt].f = from; 35 ans[cnt++].s = to; 36 degree[to]--; 37 XOR_sum[to] ^= from; // 异或性质 38 if (degree[to] == 1) 39 q.push(to); 40 } 41 } 42 printf("%d ", cnt); 43 for (int i = 0; i < cnt; i++) 44 printf("%d %d ", ans[i].f, ans[i].s); 45 } 46 return 0; 47 }