前言:这两天着手做毕设,在今年的研究生数学建模的基础上研究“大数据下多流形聚类分析”问题,导师要求我这周把每一个算法的实现对比一下效果展示给他看,表示今天google的搜索结果中没有找到诸如SSC的函数教程,又养成了不copy代码的习惯,那就自己从头开始学呗,刚好mathworks上面提供一篇详细的聚类分析的教程,特此翻译一下,希望自己和读者都能更好的咬文嚼字,以作为未来几天高维度数据matlab聚类实现的热身运动。
下面的例子将演示如何使用Matlab内的统计和机器学习工具箱中的聚类分析算法检验观测值或对象之间的异同。俗话说的好:“物以类聚,人以群分”。不管是人还是物总是呈现出抱团或者集群的状态;其中,相同的种类集群对象的特征是相似的,不同簇对象的特性不一致。
本文内容如下:
- K均值和层次聚类
- 费雪鸢尾花数据
- 对费雪鸢尾花数据进行K-均值聚类
K均值和层次聚类
统计和机器学习工具箱中有两个聚类算法的函数实现,分别是:K均值和层次聚类算法。
K-均值聚类算法是会把数据中的观测值作为拥有位置和观测值之间的距离的对象来划分,也就是说该算法会根据对象的位置和对象间的距离来决定聚类结果。
层次聚类算法是一种对每一个观察值进行分组观察的算法,该算法会在各种距离的基础上创建一个集群树。这棵树不同于单一类集合的K-均值聚类,它神奇的地方在于其“多层次结构”,也就是说某一个级别的不同类可能会在下一个更高级别中被聚为一类。意味着你可以根据你的应用选择最适合的聚类规模——“聚类之树”的大小和高度。
在本次示例使用的函数中会调用Matlab内置函数rng来生成随机数。因此为了让本次示例中的结果一致,你应该通过执行以下命令来设置随机种子控制随机数的产生。如果你不设置成相同的随机状态将会导致一些不必要的麻烦,例如,你可能看发现集群的编号顺序不同;还有就是可能会导致一个非最优的聚类结果(本次示例包含非最优聚类结果探讨以及避免该结果的方法)。
rng(14,'twister');
译者注:由于我的Matlab属于早期版本R2010a,因此没有内置随机数控制器rng函数;故各位使用早期版本的同志可以通过如下方式设置随机种子,详情见官网解释:
rand('twister',14);
费雪鸢尾花数据
在20世纪20年代,植物学家埃德加·安德森集从鸢尾花样本中测量了三个不同品种的鸢尾花萼片长宽和花瓣长宽的数据,其中每个种类分别有50个小样本。该测量数据被称为费雪鸢尾花数据或安德森鸢尾花数据。
在这些数据中的各个观测值都来自于已知物种,因此能够很清晰的将这些数据进行分组。现在,我们将忽略数据中的品种信息,只使用原始的测量数据来对观测值进行聚类。当我们完成聚类的时候,就可以将所得的聚类结果与实际物种分类结果进行对比,以查看鸢尾花的三个种类是否表现出明显的个性特征。
对费雪鸢尾花数据进行K-均值聚类
函数kmeans实现K-均值聚类,通过使用迭代算法让所有观测值分配到类中,使得每一个对象到对应类的质心的距离之和最小。该方法应用于本次的费雪鸢尾花数据时,将能够很自然的根据数据中的萼片和花瓣的测量数据对鸢尾花样本进行种类分组。使用K-均值聚类的时候,你必须要指定聚类数。
首先,加载数据然后调用函数kmeans,该函数指定了希望聚类的数量为2,并使用(平方)欧式距离计算点到质心的距离。你可以绘制轮廓图来更好的知道聚类分离的效果,轮廓图显示的是观察值到同一类内的点之间的距离与到其他类内的点之间的距离的对比。
load fisheriris % 加载数据到矩阵变量meas到向量species中 [cidx2,cmeans2] = kmeans(meas,2,'dist','sqeuclidean'); % 参数‘dist’的值为‘sqeuclidean’ [silh2,h] = silhouette(meas,cidx2,'sqeuclidean'); % 绘制轮廓图并返回轮廓值到si1h2
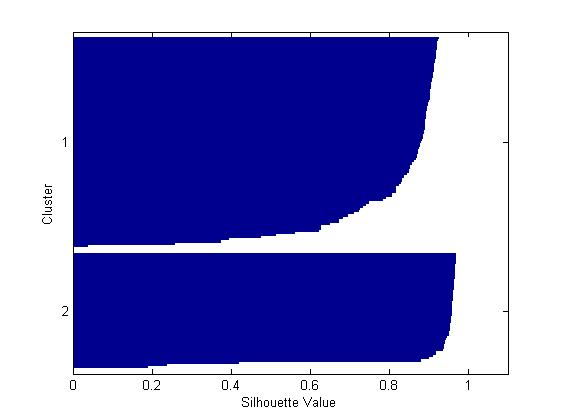
从上面所示的轮廓图可以你可以看到,两类中大部分的点都有很高的轮廓值(大于0.8),说明这些点能够从临近的群中很好的分离出来,但是每一个类中同样有少部分点的轮廓值是比较低的,表明他们很接近其他类的点,很容易与其他类的点混淆,其特征不够明显。
事实表明,数据中的第四个测量变量——花瓣宽度与第三个测量变量花瓣长度之间的关系相当紧密。因此,我们可以在不考虑第四个测量变量的情况下根据前三个变量数据绘制出一个展示效果良好的三维图。如果根据k-均值聚类的结果给每一个类的数据用不同的符号表示绘制散点图,你将会很方便的识别出那些轮廓值低的点,因为这些点与其他类的点靠在一起。
ptsymb = {'bs','r^','md','go','c+'};
for i = 1:2
clust = find(cidx2==i);
plot3(meas(clust,1),meas(clust,2),meas(clust,3),ptsymb{i}); % 使用蓝色方块和红色三角形分别标记2类的观察值
hold on
end
plot3(cmeans2(:,1),cmeans2(:,2),cmeans2(:,3),'ko');
plot3(cmeans2(:,1),cmeans2(:,2),cmeans2(:,3),'kx'); % 使用符号来标记两个类的质心
hold off
xlabel('Sepal Length'); % 标记x轴
ylabel('Sepal Width');
zlabel('Petal Length');
view(-137,10); % 旋转
grid on % 添加网格
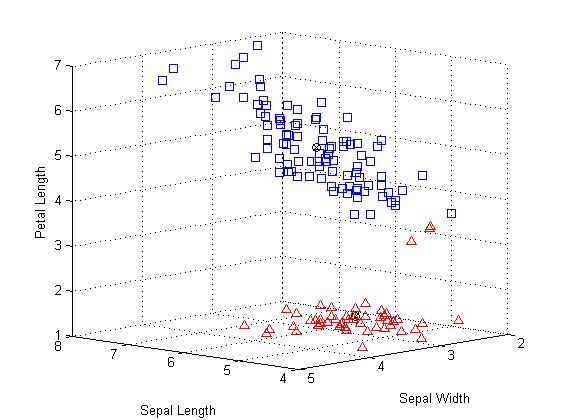
上图中,很明显的有上下两个类;且使用圆叉符号标记每一个类的质心。其中属于下层的有3个使用三角形标记的观察值非常靠近上层中使用正方形标记的群集。但是,实际上,由于上部分的类展开的比较分散,因此那3个点相对于上面的类而言跟接近下面的类的质心,即使他们与被划分的那一个类别之间被一条沟分离。由于k-均值聚类只考虑距离而不是密度,也就使得这样的聚类结果产生。
你可以通过增加簇的数目来查看kmeans函数是否可以从数据中找到进一步的分组结构。这一次,我们使用可选参数“display”打印出聚类算法在每一次迭代过程中的详细信息。
[cidx3,cmeans3] = kmeans(meas,3,'display','iter');

在每一次迭代中,k均值算法都会重新类内的点以降低点到质心之间的距离之和,然后为新的类的划分重新计算聚类中心。注意在每一次迭代后重新分配的观察值的数目都会减少直到距离之和达到最小值的时候质心稳定,不再需要重新聚类。在本次示例中k均值算法由两个阶段组成,第二阶段不再进行任何重新分配,表明第一阶段经过3此迭代后达到最小值78.8514。
默认情况下,k均值算法会使用随机选择的初始质心位置处开始聚类过程。正如其他类型的数值最小化算法一样,k均值算法要想达到距离最小值有时候取决于初始点的选定;并且有可能因此只会收敛到局部最小值,这就会造成分配点到某一个类的时候计算的该点到质心的聚类之和相对来说不是全局最小值,从而因此错过更好的聚类结果。好消息是你可以指定可选参数“replicates”来解决这一问题。当你指定该参数为1以上的时候,k均值算法将会为每一次重复聚类选定不同的随机产生的质心开始聚类过程。
[cidx3,cmeans3,sumd3] = kmeans(meas,3,'replicates',5,'display','final'); % 指定重复5次选取初始质心
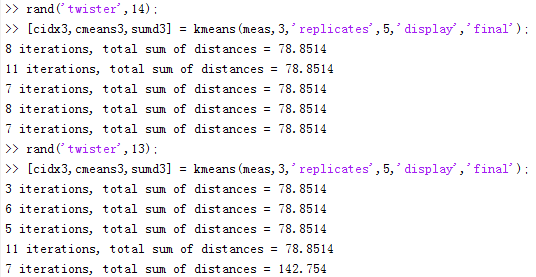
这里告诉我们,随机种子的设定非常重要,一旦随机子不同,选取的随机数就不同,造成不同的初始点选定。其中,在选定随机种子为13的时候,在重复第5次聚类过程经过7次迭代,出现了局部最小值为142.754。因此,对于这个简单的示例,非全局最小值仍然存在。其中,第三个输出参数“sumd3”包含了最佳聚类方案的每一个类内距离之和数据。
sum(sumd3) % 对类内距离之和求和

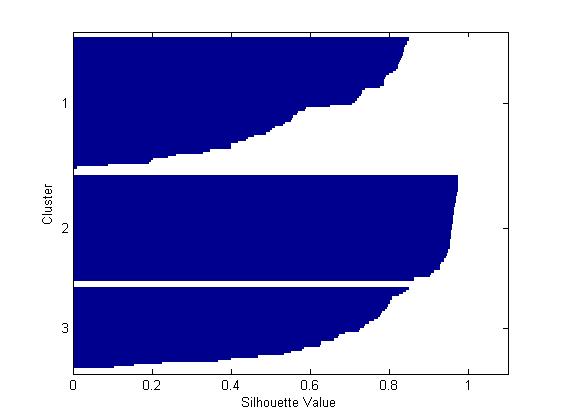
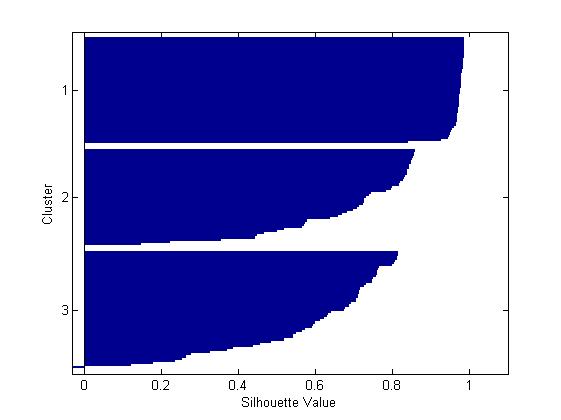
为这个聚为3类的解决方案绘制轮廓图,该图表明有一个类能够很好的从其他类中分离,但是另外两个类区分的并不是很明显。
[silh3,h] = silhouette(meas,cidx3,'sqeuclidean');
你还可以通过再次绘制原始数据的散点图观察点的聚类情况。
for i = 1:3
clust = find(cidx3==i);
plot3(meas(clust,1),meas(clust,2),meas(clust,3),ptsymb{i});
hold on
end
plot3(cmeans3(:,1),cmeans3(:,2),cmeans3(:,3),'ko');
plot3(cmeans3(:,1),cmeans3(:,2),cmeans3(:,3),'kx');
hold off
xlabel('Sepal Length');
ylabel('Sepal Width');
zlabel('Petal Length');
view(-137,10);
grid on
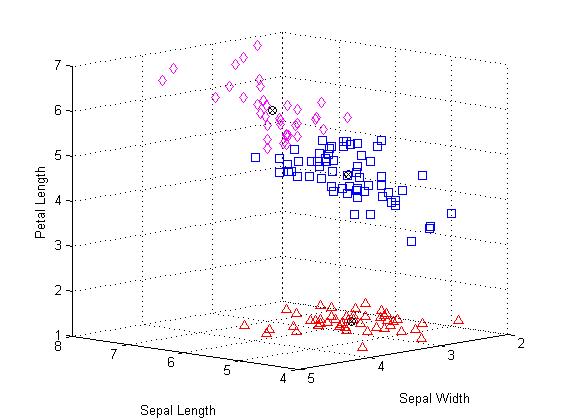
由上图可以发现原来属于上面的那个类被聚为两个类别,并且这两个类里面的观察值彼此之间挨得很紧密。当然,这三个聚类结果相对于前面的两个聚类结果而言是否对你有用取决于你的打算。函数“silhouette”的第一个输出参数包含每一个点的轮廓值,根据轮廓值的均值结果对比可知轮廓均值较大的那个解决方案即聚为两类相对来说更合理。
[mean(silh2) mean(silh3)]

你也可以使用不同的距离指标来对这些数据重新聚类。余弦距离来评估这些数据的相似性使用可能更有意义,因为它会只考虑数据的相对大小而忽略测量数据的绝对大小。因此,两个花朵的大小不一,但拥有相同形状的花瓣和萼片,使用欧式距离就无法决定它们相似但是使用余弦距离却可以下出这两朵花相似的结论。
[cidxCos,cmeansCos] = kmeans(meas,3,'dist','cos');
从剪影图的现实结果来看,余弦距离相对欧式距离的聚类结果似乎只显示出轻微的较好的分离效果。
[silhCos,h] = silhouette(meas,cidxCos,'cos'); [mean(silh2) mean(silh3) mean(silhCos)]

注意,本次聚类的类别编号和上一次聚类的编号不同,这是因为k均值算法随机的选择初始值。通过绘制原始数据散点图,可以看出使用不同距离创建的群集形状的差异。这两种聚类的结果相似,但是使用余弦距离处理的处于坐标上方的两个簇集合形状彼此之间互相渗透,互相延伸。
for i = 1:3
clust = find(cidxCos==i);
plot3(meas(clust,1),meas(clust,2),meas(clust,3),ptsymb{i});
hold on
end
hold off
xlabel('Sepal Length');
ylabel('Sepal Width');
zlabel('Petal Length');
view(-137,10);
grid on

上图并没有画出质心,因为余弦距离质心对应于原始数据空间中原点上的的射线(这句话目前不能理解)。然而,你可以在平行坐标轴上绘制标准化后的数据散点图进而可视化聚类中心之间的差异。
lnsymb = {'b-','r-','m-'};
names = {'SL','SW','PL','PW'};
meas0 = meas ./ repmat(sqrt(sum(meas.^2,2)),1,4); % 将每一个数据除以数据进行平方求和开根号后的结果从而达到标准化
ymin = min(min(meas0));
ymax = max(max(meas0));
for i = 1:3
subplot(1,3,i);
plot(meas0(cidxCos==i,:)',lnsymb{i});
hold on;
plot(cmeansCos(i,:)','k-','LineWidth',2);
hold off;
title(sprintf('Cluster %d',i));
xlim([.9, 4.1]);
ylim([ymin, ymax]);
% 以下部分在R2010a版本中运行不出
h_gca = gca;
h_gca.XTick = 1:4;
h_gca.XTickLabel = names;
end

译者注:可能是Matlab的版本原因,导致定义结构化数据h_gca的时候报错,并且横坐标的刻度的label也没有成功标记,因此该部分代码修改如下:
set(gca,'XTick',1:4); set(gca,'XTickLabel',names);
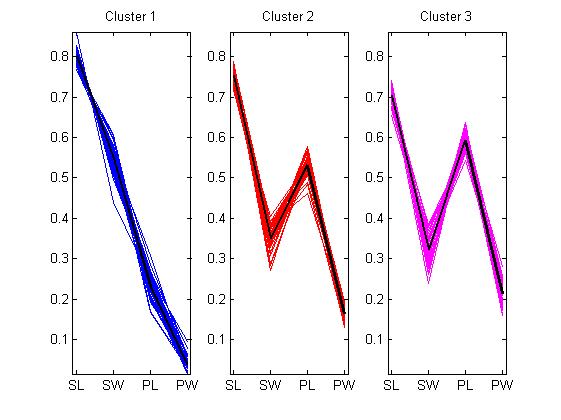
上图清晰的表明,三个簇中平均每一个花朵样品的花瓣和萼片大小都不同。第一簇中的花瓣比他们的萼片严格小(严格递减)。后面两类的花瓣和萼片的大小都有重叠部分,也就是说后面两类的部分花瓣和萼片大小差不多,但是第三类比第二类重叠的部分更多。你也可以看出第二类和大三类的样品的属性非常相似。
因为实际上的数据样本中每一个观察值所属的种类都是已知的,因此可以通过将k均值聚类结果和实际分类结果对比发现这三个物种之间是否存在可以用来区分的物理特性。事实上,正如下图所示,使用余弦距离创建的类于实际分组不同的观察值只有5个,这5个用星星标记的点都处于坐标系上方两个类之间的边界附近。
subplot(1,1,1);
for i = 1:3
clust = find(cidxCos==i);
plot3(meas(clust,1),meas(clust,2),meas(clust,3),ptsymb{i});
hold on
end
xlabel('Sepal Length');
ylabel('Sepal Width');
zlabel('Petal Length');
view(-137,10);
grid on
sidx = grp2idx(species);
miss = find(cidxCos ~= sidx);
plot3(meas(miss,1),meas(miss,2),meas(miss,3),'k*');
legend({'setosa','versicolor','virginica'});
hold off

译者注:原网站的部分图片出现错误,本次翻译都已经改正;所有代码均在Matlab2010a版本上运行无误,如有翻译不当地方,欢迎指正。关于第二个层次聚类方法,后面将会继续更——使用费雪鸢尾花数据实现层次聚类。