[SDOI2012]任务安排
斜率优化入门题:
设(f(x))为(F(x))的后缀和,(t(x))为(T(x))的前缀和。(dp(i))表示完成到第(i)任务的最小代价,转移:
(dp(i)=min {dp(j) +f(j+1) imes(S+t(i)-t(j)) })
拆掉:
- 和(j)无关: 没有
- 只和(j)相关:(dp(j)+f(j+1) imes(S-t(j)))
- 和(i,j)相关:(f(j+1) imes t(i))
我们发现只和(j)相关的可以直接预处理,现在的问题是确定了(i)如何快速找到一个(j)
令(y_j=dp(j)+f(j+1) imes(S-t(j))),(x_j=f(j+1)),原式可以写成:
[dp(i)= y_j+x_jt(i)
]
转换一下式子
[y_j=-t(i)x_j+dp(i)
]
现在问题就变成了确定了一个(i),要快速查询前面的一个(j)使得(dp(i))最小
把这个东西看成一条直线,就变成了我有一条在平面上平移的斜率为(-t(i))的直线,现在要找一个点((x_j,y_j))使得过这个点的斜率为(-t(i))的直线的截距尽量小。
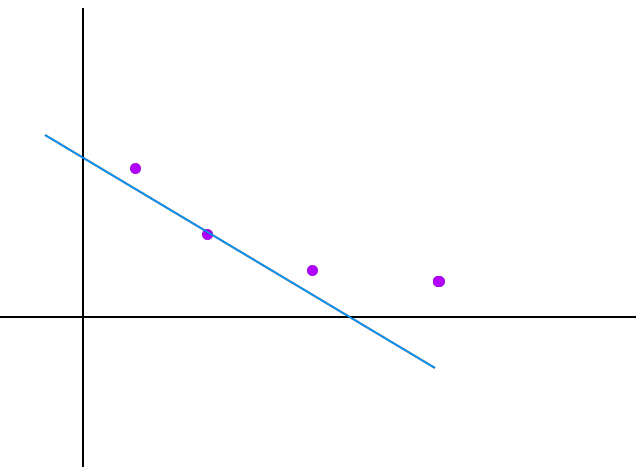
蓝线:斜率为(-t(i))的线
紫点:((x_j,y_j))
很明显,可以看做有一条在(y)负半轴无限远处有一条直线慢慢上移(截距慢慢变大),这条直线突然经过一个我们集合内的点时,它此时的截距就是最小的截距。很显然,这个点一定在凸包上面,而且这个点左右两边的斜率一定是左边更小,右边更大(斜率是负数)。
动态维护一下凸包就好了。
//@winlere
#include<iostream>
#include<cstdio>
#include<cstring>
#include<algorithm>
using namespace std; typedef long long ll;
inline int qr(){
register int ret=0,f=0;
register char c=getchar();
while(c<48||c>57)f|=c==45,c=getchar();
while(c>=48&&c<=57) ret=ret*10+c-48,c=getchar();
return f?-ret:ret;
}
int n,s;
const int maxn=3e5+5;
int Ti[maxn],Fi[maxn];
ll st[maxn],sf[maxn];
ll x[maxn],y[maxn],q[maxn],dp[maxn];
int cnt;
inline ll getval(const int&i,const int&j){
return dp[j]+sf[j+1]*(s+st[i]-st[j]);
}
inline bool chek0(const int&i,const int&j,const ll&k){
return (long double)1.0*((y[i]+dp[i])-(y[j]+dp[j]))*(x[i]-x[k])<=(long double)1.0*((y[i]+dp[i])-(y[k]+dp[k]))*(x[i]-x[j]);
}
inline bool chek(const int&i,const int&j,const ll&k){
return (long double)1.0*(y[i]+dp[i])-(y[j]+dp[j])<=(long double)1.0*k*(x[i]-x[j]);
}
inline int lookup(const ll&k){
register int l=1,r=cnt-1,ret=cnt,mid;
while(l<=r){
mid=(l+r)>>1;
if(chek(q[mid],q[mid+1],k))
r=mid-1,ret=mid;
else l=mid+1;
}
return q[ret];
}
int main(){
n=qr();s=qr();
for(register int t=1;t<=n;++t)
Ti[t]=qr(),Fi[t]=qr(),st[t]=st[t-1]+Ti[t];
for(register int t=n;t>=0;--t) sf[t]=sf[t+1]+Fi[t];
for(register int t=0;t<=n;++t) y[t]=sf[t+1]*(s-st[t]),x[t]=sf[t+1];
q[cnt=1]=0;
for(register int t=1;t<=n;++t){
dp[t]=getval(t,lookup(-st[t]));
while(cnt>1&&chek0(q[cnt-1],q[cnt],t)) --cnt;
q[++cnt]=t;
}
cout<<dp[n]<<endl;
return 0;
}