用G2O来拟合曲线,拟合模型:y = exp(a*x*x + b*x + c);
首先利用opencv产生随机数,x_data, y_data;同时我们把随机数写入txt,通过matlab来拟合检验
#include <iostream> #include<fstream> #include<iomanip> #include <g2o/core/base_vertex.h> #include <g2o/core/base_unary_edge.h> #include <g2o/core/block_solver.h> #include <g2o/core/optimization_algorithm_levenberg.h> #include <g2o/core/optimization_algorithm_gauss_newton.h> #include <g2o/core/optimization_algorithm_dogleg.h> #include <g2o/solvers/dense/linear_solver_dense.h> #include <Eigen/Core> #include <opencv2/core/core.hpp> #include <cmath> #include <chrono> using namespace std; // 曲线模型的顶点,模板参数:优化变量维度和数据类型 class CurveFittingVertex: public g2o::BaseVertex<3, Eigen::Vector3d> { public: // Eigen库为了使用SSE加速,所以内存分配上使用了128位的指针 EIGEN_MAKE_ALIGNED_OPERATOR_NEW// 参考 https://blog.csdn.net/rs_huangzs/article/details/50574141 virtual void setToOriginImpl() // 顶点重置 { _estimate << 0,0,0; } virtual void oplusImpl( const double* update ) // 顶点更新,X_k+1 = X_k + X_delta { _estimate += Eigen::Vector3d(update); } // 存盘和读盘:留空 virtual bool read(istream& in) { return 0; } virtual bool write( ostream& out ) const { return 0; } }; // 误差模型 模板参数:观测值维度,类型,连接顶点类型 class CurveFittingEdge: public g2o::BaseUnaryEdge<1,double,CurveFittingVertex> { public: EIGEN_MAKE_ALIGNED_OPERATOR_NEW CurveFittingEdge( double x ): BaseUnaryEdge(), _x(x) {} // 计算曲线模型误差 void computeError() { const CurveFittingVertex* v = static_cast<const CurveFittingVertex*> (_vertices[0]); const Eigen::Vector3d abc = v->estimate(); _error(0,0) = _measurement - std::exp( abc(0,0)*_x*_x + abc(1,0)*_x + abc(2,0) ); } virtual bool read( istream& in ) { return 0; } virtual bool write( ostream& out ) const { return 0; } public: double _x; // x 值, y 值为 _measurement }; int main( int argc, char** argv ) { // 产生带噪声的数据 double a=1.0, b=2.0, c=1.0; // 真实参数值 int N=100; // 数据点 double w_sigma=1.0; // 噪声Sigma值 cv::RNG rng; // OpenCV随机数产生器 double abc[3] = {0,0,0}; // abc参数的估计值 vector<double> x_data, y_data; // 数据 cout<<"generating data: "<<endl; for ( int i=0; i<N; i++ ) { double x = i/100.0; x_data.push_back ( x ); y_data.push_back ( exp ( a*x*x + b*x + c ) + rng.gaussian ( w_sigma ) ); cout<<x_data[i]<<" "<<y_data[i]<<endl; } //将数据写入文本 //创建文件 fstream f("file_1.txt", ios::out); if (f.bad()) { cout << "打开文件出错" << endl; return 0; } //写入x for (size_t i = 0; i < x_data.size(); i++) { f << x_data[i] << " "; } f << endl;//换行 //写入y for (size_t i = 0; i < y_data.size(); i++) { f << y_data[i] << " "; } //关闭文件 f.close(); // 构建图优化,先设定g2o typedef g2o::BlockSolver< g2o::BlockSolverTraits<3,1> > Block; // 每个误差项优化变量维度为3,误差值维度为1 Block::LinearSolverType* linearSolver = new g2o::LinearSolverDense<Block::PoseMatrixType>(); // 线性方程求解器 Block* solver_ptr = new Block( linearSolver ); // 矩阵块求解器 // 梯度下降方法,从GN, LM, DogLeg 中选 g2o::OptimizationAlgorithmLevenberg* solver = new g2o::OptimizationAlgorithmLevenberg( solver_ptr ); //g2o::OptimizationAlgorithmGaussNewton* solver = new g2o::OptimizationAlgorithmGaussNewton(solver_ptr); //g2o::OptimizationAlgorithmDogleg* solver = new g2o::OptimizationAlgorithmDogleg(solver_ptr); g2o::SparseOptimizer optimizer; // 图模型 optimizer.setAlgorithm( solver ); // 设置求解器 optimizer.setVerbose( true ); // 打开调试输出 // 往图中增加顶点 CurveFittingVertex* v = new CurveFittingVertex(); v->setEstimate( Eigen::Vector3d(0,0,0) );//猜想初始值 v->setId(0); optimizer.addVertex( v ); // 往图中增加边 for ( int i=0; i<N; i++ ) { CurveFittingEdge* edge = new CurveFittingEdge( x_data[i] ); edge->setId(i); edge->setVertex( 0, v ); // 设置连接的顶点 // set the ith vertex on the hyper-edge to the pointer supplied edge->setMeasurement( y_data[i] ); // 观测数值 edge->setInformation( Eigen::Matrix<double,1,1>::Identity()*1/(w_sigma*w_sigma) ); // 信息矩阵:协方差矩阵之逆 optimizer.addEdge( edge ); } // 执行优化 optimizer.initializeOptimization(); optimizer.optimize(100); // 输出优化值 Eigen::Vector3d abc_estimate = v->estimate(); cout<<"estimated model: "<<abc_estimate.transpose()<<endl; return 0; }
g2o拟合结果:
a = 0.890911;
b = 2.1719;
c = 0.943629;
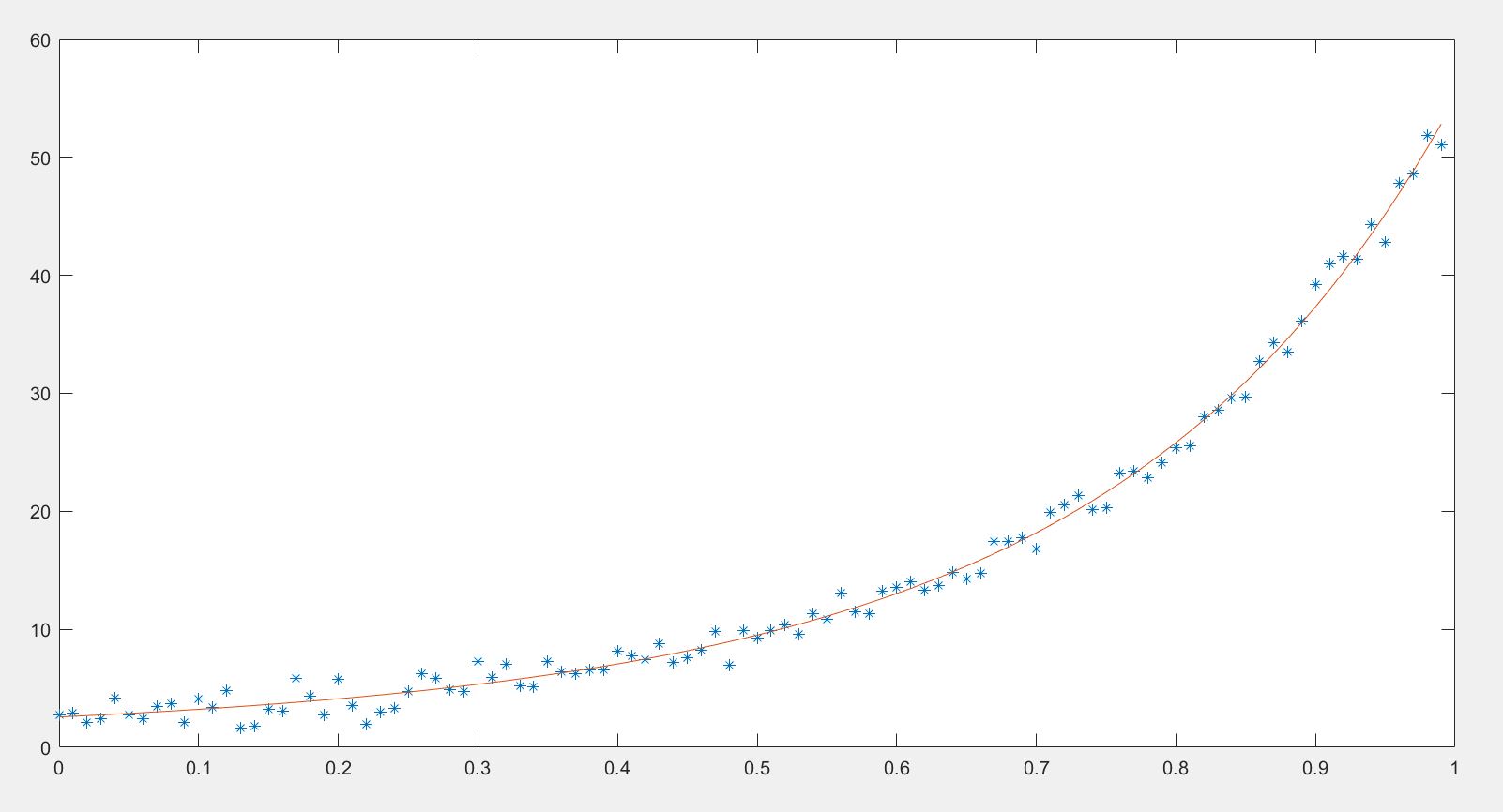
我们基于此,利用如下matlab代码,将随机数和G2O拟合结果可视化
%%clear all close all clc load file_1.txt %% 待拟合数据 temp = file_1; x1 = temp(1,:); y1 = temp(2,:); plot(x1,y1,'*'); hold on; %% plot the results of G2O syms x; a = 0.890911; b = 2.1719; c = 0.943629; x = 0:0.01:0.99; y = zeros(1,100); [m,n] = size(x); for i = 1:1:n y(i) = exp( a*x(i)*x(i) + b*x(i) + c ); end plot(x,y);
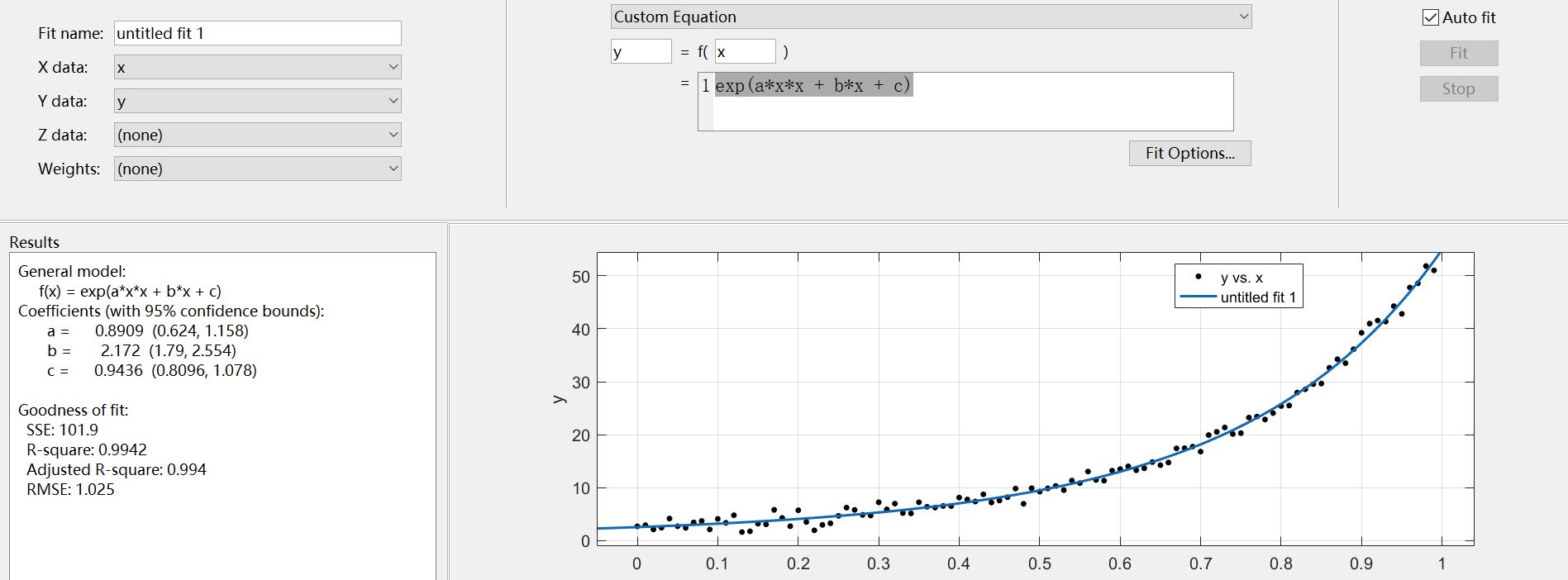
最后,再看看matlab拟合工具箱拟合结果(其实工具箱强得一笔,随便用其他模型也能达到完美得置信区间和残差):