POJ

（点击此处查看原题）

题意

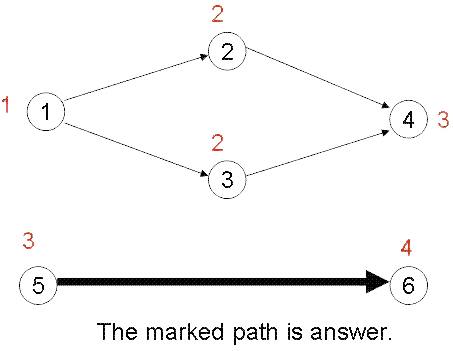
给出一个有n个结点，m条边的DAG图，每个点都有权值，每条路径（注意不是边）的权值为其经过的结点的权值之和，每条路径总是从入度为0的点开始，直至出度为0的点，问所有路径中权值最大者为多少，如下图，加粗的为权值最大者：

解题思路

这是在一个无起点、终点的图中的求最长路的问题，因此无法像一般的最长路问题那样求解。

首先，因为图中只存在点权，为了方便，我们一般将点权转化为边权：取每条边的权值为其终点的权值，将点权转化为边权。

然后，由于我们每条路径都是以入度为0的点开始，以出度为0的点结束，而且是求最大路，我第一想法就是AOV网中求事件的最晚完成时间，这两者是很相似的，不同的在于AOV网中有一个入度为0的源点和一个出度为0的汇点，而这个地方有多个入度为0的点和多个出度为0的点，不过实际的操作是完全一致的，都是利用拓扑排序的效果求最长路

为了方便理解，可以假设存在一个权值为0的点s向所有入度为0的点建边，然后把这个点当作起点，利用求拓扑序的时候，可以求出事件的最晚完成时间的效果，求其余各点到这个点的最长路，最后求出所有出度为0的点到s的最长路中的最大者，即为答案

代码区

#include<iostream>
#include<cstdio>
#include<algorithm>
#include<cstring>
#include<queue>
#include<string>
#include<fstream>
#include<vector>
#include<stack>
#include <map>
#include <iomanip>

#define bug cout << "**********" << endl
#define show(x, y) cout<<"["<<x<<","<<y<<"] "
#define LOCAL = 1;
using namespace std;
typedef long long ll;
const ll inf = 1e18+10;
const ll mod = 1e9 + 7;
const int Max = 1e6 + 10;
const int Max2 = 3e2 + 10;

struct Edge
{
    int to,next;
    ll dis;
}edge[Max<<1];

int n, m;
ll val[Max];
int head[Max],tot;
int topo[Max],id;            //记录每个点的拓扑序
int d_in[Max],d_out[Max];    //记录每个点的入度和出度
ll dist[Max];                //距离源点的最大距离

int init()
{
    memset(head,-1,sizeof(head));
    tot = 0;
    memset(topo,0,sizeof(topo));
    id = 0;
    memset(d_in,0,sizeof(d_in));
    memset(d_out,0,sizeof(d_out));
}

void add(int u,int v,ll dis)
{
    edge[tot].to = v;
    edge[tot].dis = dis;
    edge[tot].next = head[u];
    head[u] = tot++;
}

void topoSort()
{
    queue<int>q;                        //存储入度为0的点
    for(int i = 1;i <= n ;i ++)
    {
        if(d_in[i] == 0)
        {
            q.push(i);
            dist[i] = val[i];            //初始化
        }
    }
    while(!q.empty())
    {
        int u = q.front();q.pop();
        topo[u] = ++id;
        for(int i = head[u] ; i != -1 ; i = edge[i].next)
        {
            int v = edge[i].to;
            ll dis = edge[i].dis;
            if(!topo[v])
            {
                d_in[v] --;
                dist[v] = max(dist[v],dist[u] + dis);
                if(d_in[v] == 0)
                    q.push(v);
            }
        }
    }

}

int main()
{
#ifdef LOCAL
    //        freopen("input.txt", "r", stdin);
    //        freopen("output.txt", "w", stdout);
#endif
    while(scanf("%d%d",&n,&m)!=EOF)
    {
        init();
        for(int i = 1;i <= n ;i ++)
            scanf("%lld",val+i);
        for(int i = 1, u, v ; i <= m ;i ++)
        {
            dist[i] = -inf;
            scanf("%d%d",&u,&v);
            d_out[u] ++;
            d_in[v]++;
            add(u,v,val[v]);        //以终点的权值作为边的权值
        }
        topoSort();
        ll max_dis = -inf;
        for(int i = 1;i <= n ;i ++)
        {
            if(d_out[i] == 0)            //只对出度为0的点进行判断
            {
                max_dis = max(max_dis,dist[i]);
            }
        }
        printf("%lld
",max_dis);
    }
    return 0;
}