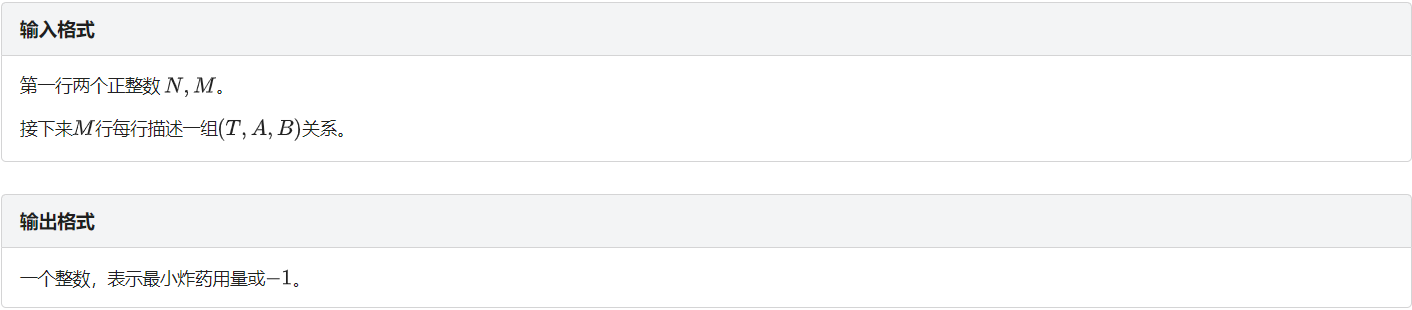
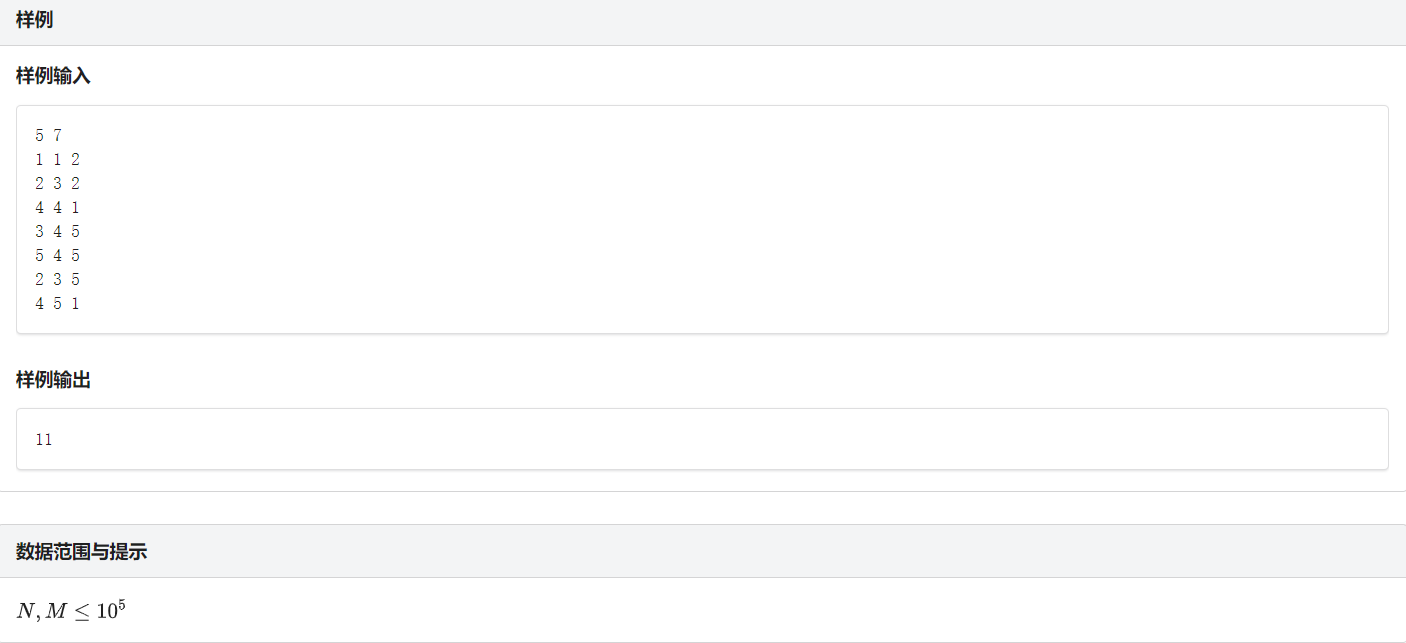
题目:

分析:
看到题目之后,第一感觉:这不是非常板子的差分约束嘛?直接把边加好之后,然后跑个最长路,当然最长路就不写dij了,搞个spfa,tle了?双端队列优化(如果新加入的元素>=队首元素,直接加前面,否则加在后面,注意判空),然后就这样过了,时间也是很可观.
当然为了更方便的处理我们建了节点0与所有的点连边权为0的边,且dis[0]=1.直接就符合题意了.
spfa代码(先别走,还没到正题)
#include <cstdio> #include <string> #include <queue> #include <cstring> using namespace std; const int maxn=1e5+10; deque<int> qu; int rd[maxn]; struct E{ int to,next,val; }ed[maxn*3];//开出自己虚拟的边 int head[maxn],tot; void J(int a,int b,int c){ ed[++tot].to=b; ed[tot].val=c; ed[tot].next=head[a]; head[a]=tot; } int vis[maxn],ha[maxn],dp[maxn]; int main(){ int n,m; scanf("%d%d",&n,&m); int t,js1,js2; for(int i=1;i<=n;i++) J(0,i,0);//虚拟的边 dp[0]=1;//最小为1 for(int i=1;i<=m;i++){//对约束进行处理 scanf("%d%d%d",&t,&js1,&js2); if(t==1){J(js1,js2,0);J(js2,js1,0);} if(t==2) J(js1,js2,1); if(t==3) J(js2,js1,0); if(t==4) J(js2,js1,1); if(t==5) J(js1,js2,0); } qu.push_front(0); while(!qu.empty()){ int x=qu.front(); qu.pop_front(); vis[x]=0; for(int i=head[x];i;i=ed[i].next){ if(dp[ed[i].to]<dp[x]+ed[i].val){ dp[ed[i].to]=dp[x]+ed[i].val; if(!vis[ed[i].to]){ vis[ed[i].to]=1; ha[ed[i].to]++; if(!qu.empty()&&dp[ed[i].to]>=dp[qu.front()]) qu.push_front(ed[i].to); else qu.push_back(ed[i].to);//双端队列优化 } if(ha[ed[i].to]>=n){printf("-1");return 0;}//正环 } } } long long ans=0; for(int i=1;i<=n;i++) ans+=(long long)dp[i]; printf("%lld",ans); return 0; }
spfa终究是不稳定的算法,没准那天就开始卡各种优化了,至少裸的spfa已经卡了很多了.所以我们考虑换一种做法.
首先我们先想如果没有1,3,5,只有2,4这些操作我们怎么办(别再spfa啦),非常简单直接拓扑排序顺便dp一下就完了,如果有环肯定就可以直接输出-1了(毕竟有环就是正环).
然后我们再考虑加上操作1,这时的环不一定是正环了,直接拓扑排序就会把一些不应该是-1的判断为-1,但是我们可以这样想,1所连的所有的点都是相等的,直接搞个并查集就好了,最后把相等的点缩成一个,这样就很好的避免了0环的干扰.有环就又是正环了,然后就是,拓扑排序了.
最后还有两个操作3,5,这两个既加的边权为0,有不能保证连接的两点相等,不过你会发现,其实0的边是可以存在的,只要规避一下0的环就好了,0的环能不能直接缩成一个点呢?我们来证明一下.
首先先说明这里的环指的是强连通分量.
如果点u,v属于同一个联通分量(由0的边组成的),那么就有u到v有路径,当然0边权的边组成的路径边权和是0,这也就有val[u]<=val[v],同理val[v]<=val[u],于是有val[v]==val[u],也就是说同一由权值为0的边组成的强连通分量里,所有的点权相等.那么就直接缩成一个点就好了,其实操作1的也是类似的,直接用这种缩点就好了.
这时我们就会得到一个新的图,这个图有什么性质呢?如果有环,必为正环,也就是说这时我们就可以拓扑排序了,排完之后,所有的得到的dp[i]乘上联通分量i的节点的个数的和就是答案了.(当然节点个数要提前处理出来)
然后一些细节:
没必要建一个只有0边权的图,tarjan的时候continue掉不合法的边就行了.
不要建同一强连通分量里0的边,否则就又有0的环了.
不要忘掉同一强连通分量里为1的边,否则会丢掉一些正环.
代码:
#include <cstdio> #include <queue> using namespace std; const int maxn=1e5+10; queue<int> qu; int rd[maxn];//入度 struct E{ int to,next,val; }ed[maxn*2]; int head[maxn],tot; void J(int a,int b,int c){ ed[++tot].to=b; ed[tot].val=c; ed[tot].next=head[a]; head[a]=tot; } int js,dfn[maxn],low[maxn],q,bel[maxn],sta[maxn],top,gs[maxn]; //上面变量分别表示dfs的次数记录,时间戳,tarjan追溯值,强连通分量的个数,某个节点属于哪个强连通分量 //跑tarjan用的栈,栈顶,某个强联通分量的节点个数 void tarjan(int x){//tarjan板子 low[x]=dfn[x]=++js;sta[++top]=x; for(int i=head[x];i;i=ed[i].next){ if(ed[i].val==1) continue; if(!dfn[ed[i].to]){tarjan(ed[i].to);low[x]=min(low[ed[i].to],low[x]);} else if(!bel[ed[i].to]) low[x]=min(dfn[ed[i].to],low[x]); } if(low[x]==dfn[x]){ q++;int tm; do{gs[q]++;tm=sta[top--];bel[tm]=q;}while(tm!=x); } } E ed0[maxn*2];//新图的边 int head0[maxn],tot0,dp[maxn]; void J0(int a,int b,int c){ ed0[++tot0].to=b; ed0[tot0].val=c; ed0[tot0].next=head0[a]; head0[a]=tot0; } int main(){ int n,m; scanf("%d%d",&n,&m); int t,js1,js2; for(int i=1;i<=m;i++){//对读入进行处理 scanf("%d%d%d",&t,&js1,&js2); if(t==1){J(js1,js2,0);J(js2,js1,0);} if(t==2) J(js1,js2,1); if(t==3) J(js2,js1,0); if(t==4) J(js2,js1,1); if(t==5) J(js1,js2,0); } for(int i=1;i<=n;i++) if(!dfn[i]) tarjan(i);//求强连通分量 for(int i=1;i<=n;i++) for(int j=head[i];j;j=ed[j].next) if(bel[ed[j].to]!=bel[i]||ed[j].val==1){//如果不在同一分量里或者边权为1新图加上此边 J0(bel[i],bel[ed[j].to],ed[j].val); rd[bel[ed[j].to]]++;//统计入度 } for(int i=1;i<=q;i++) if(rd[i]==0){qu.push(i);dp[i]=1;}//拓扑排序 while(!qu.empty()){ int x=qu.front();qu.pop(); for(int i=head0[x];i;i=ed0[i].next){ rd[ed0[i].to]--; dp[ed0[i].to]=max(dp[ed0[i].to],dp[x]+ed0[i].val); if(rd[ed0[i].to]==0) qu.push(ed0[i].to); } } long long ans=0; for(int i=1;i<=q;i++){ if(rd[i]){printf("-1");return 0;}//有正环(新图有环即为正环) ans+=(long long)gs[i]*(long long)dp[i]; } printf("%lld",ans); return 0; }