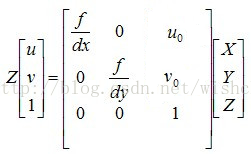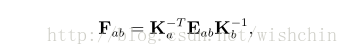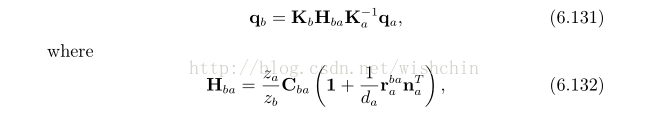从今天起,好好复习一下面试到的题目,把研究生时期学习的,工作时间忘记的东西再补回来。
本文所写与原文相距甚远,如有疑问,请拜访原文。未经允许大量盗图,如有不满,请联系删除。
原文链接:单应矩阵Homograph matrix、本质矩阵Fundamental matrix、基本矩阵essential matrix——游振兴
在单目重建中,位姿求解一般应用的为本质矩阵。 在小型室内场景重建过程中,通常状态下,使用非退化状态下两帧得到的匹配点,可以通过
公式: p2^T *F *p1=0
根据匹配对p1、p2求解F,进而求出相机位姿变换 R、t 。
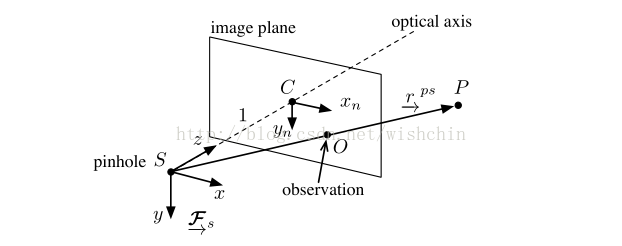
1. 透视投影/中心投影
底片生成:相机模型总结为透视投影,空间点P通过中心投影方式落到焦距 f 固定的底片上,同时丢掉了深度信息。
相机内参:定焦固定头相机会有一个固定的投影关系,其中的参数为相机内参。其他扩展功能相机的内参需要更多的信息获取。
投影模型:物体标记为稀疏点模型之后,在世界坐标系中相机以任一位姿(R,t)观察模型,总能得到唯一的二维平面点位置集合( S(p) )。
真空相机模型中,三维点集到图像底片,理论上遵循透射投影关系,相机表示为内参矩阵K,坐标转换关系为:
点集映射到底片上时丢失深度,其中f为相机焦距。dx,dy为像元尺寸,u0,v0为图像中心。 fx = f/dx ,fy = f/dy 分别为x轴和y轴上的归一化焦距。内参矩阵一般使用事先标定的方法。
2. PNP perspective-n-point
N点透视,给出一个世界坐标系标定的物体/三维点集合。依据透射关系,根据平面图像/N个二维投影点的位置来推算相机的观察者位姿,为PNP。
文章:使用OpenCV PNP
3. 核面约束
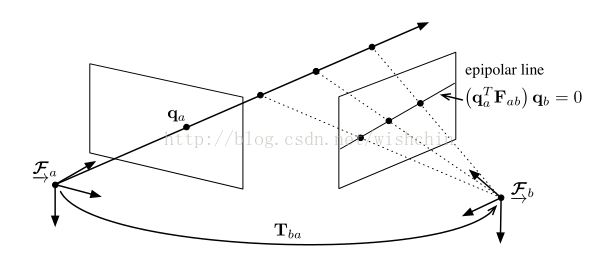
相机经过位姿转换,通过对同一个物体和同一组点观察得到两幅图像,同一组点在两幅图片中位置和顺序不同,但满足相机透视的 核面约束。
图3.1
核面约束:
上图中那个等于0的方程:p^T *F*p=0;
基本矩阵约束关系表现为:
这里的基本矩阵约束称为核线约束,如上图3.1,如果两帧之间的一个点坐标,外参矩阵已知,则空间点在另外一帧的坐标被约束在一条极线上,可以用来缩小图像匹配点的搜索范围。基本矩阵也可以用来计算内参矩阵。
求取位姿:根据一组匹配的点集和极线约束可以得到一个相对固定的位姿转换( R, t )。
本质矩阵:其中E矩阵为本质矩阵 Essential Matrix。理论上旋转、平移共有6个自由度(3个旋转,3个平移),因尺度等价,E有5个自由度(z约束为1)。求解一般使用8点法,通过SVD分解,恢复出R,t。
基本矩阵:其中F矩阵为基本矩阵 Fundamentl Matrix。根据内参矩阵和本质矩阵,解析出基本矩阵。
4. 相机外参
在小型室内场景重建过程中,通常状态下,使用非退化状态下两帧得到的匹配点,可以通过
公式: p2^T *F *p1=0
本质矩阵是相对相机位姿的简单函数:
E= S(t)R
相机运动一般很难测量,且相机有可能未被标定,不能直接用于计算本质矩阵。一般是使用八点法,在E矩阵的线性框架下求解。
5. 退化现象/斜面投影
对一个平面/一组平面上的点进行不同位姿观察,依然会得到两个投影面/两组投影点,这对应了三维稀疏场景重建?SLAM中的退化问题。
约束关系变化为:
其中H矩阵为单应矩阵Homograph Matrix。
5. 基本矩阵Fundamental Matrix、本质矩阵Essential Matrix、单应矩阵 Homograph Matrix
5.1 Essential Matrix
E= t ^ R 为3*3的矩阵,奇异值为 [ u, u, 0] ^ T 的形式。为本质矩阵的内在性质。
性质:理论上综合旋转、平移共有6个自由度,因尺度等价,E有5个自由度。
求解:一般使用8点法,通过SVD分解,恢复出R,t 。
5.2 Fundamental Matrix
基本矩阵F和E只差了一个相机内参 F = K^(-T) *E *K^(-1) ,如果需要,直接带入求解。
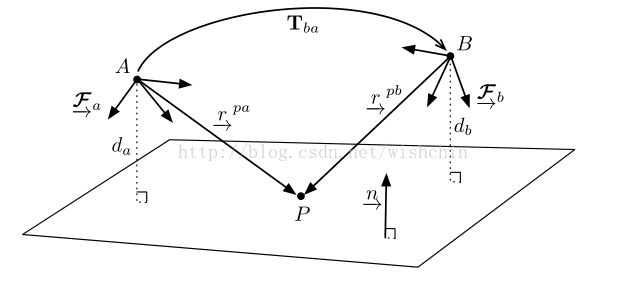
5.3 Homograph Matrix
单应矩阵的定义与R、t、平面参数相关,单应矩阵为3*3的矩阵,自由度为8,求解的思路和E、F相似。
求解:可用一组不共线的四个匹配点来计算矩阵H。
总结:
根据图像来估计位姿,一般称之为位姿追踪。非退化状态下可是根据匹配点求解Essential Matrix ,退化状态下课根据匹配点来求解 Homograph Matrix。用于实时计算位姿。