讲授卷积神经网络面临的挑战包括梯度消失、退化问题,和改进方法包括卷积层、池化层的改进、激活函数、损失函数、网络结构的改 进、残差网络、全卷机网络、多尺度融合、批量归一化等
大纲:
面临的挑战
梯度消失问题
退化问题
改进的总体思路
卷积层的改进
用矩阵乘法实现卷积运算
池化层的改进
激活函数的改进
损失函数的改进
高速公路网络
残差网络
残差网络的分析
全卷积网络
多尺度连接
批量归一化
本集总结
面临的挑战:
卷积神经网络尤其是深度卷积神经网络面临的挑战:
梯度消失问题,全连接神经网络(也叫人工神经网络ANN、多层感知器模型HLP)也提到了,BP传播时要用到f'(x),如果f'(x)<0,会越乘越小,最终梯度趋向于0,那么参数就没法更新了。
退化问题,指网络比较浅的时候,只要样本数量足够多,增加网络层数网络的精度会上升,但是要是网络达到一定层数时再增加层数网络的精度反而会下降。
过拟合问题,深度卷积神经网络一般层数比较多,宽度也比较大,每次神经元和卷积核数量也比较大,这样很容易产生过拟合问题。
计算和存储效率问题,过了追求网络精度,人们把网络做的越来越复杂,深度非常大宽度也很大,网络规模大了之后,不仅算的很慢因为运算的次数会增加,而且很占用存储空间,这样就会限制它的实际的使用。
改进的措施:
卷积层
池化层
激活函数
损失函数
网络结构
梯度消失问题:
深层网络难以训练,主要原因是梯度消失问题
X. Glorot, Y. Bengio. Understanding the difficulty of training deep feedforward neural networks. AISTATS, 2010
在实验中,分别训练了有1到5个隐含层的神经网络,激活函数使用了sigmoid,tanh等
实验结果证明,随着网络层数的增加,反向传播的作用越来越小,网络更加难以训练
激活函数的输入值容易落入饱和区间,导致过拟合
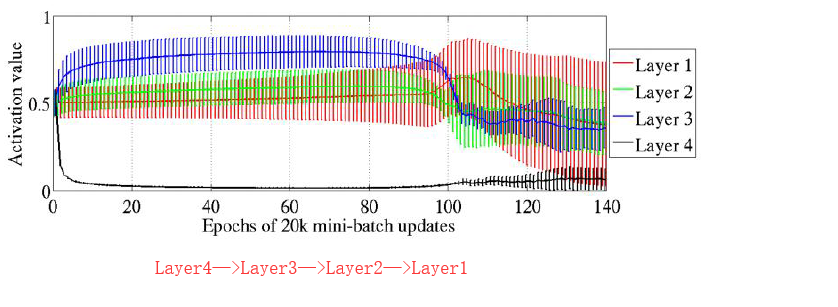
Layer4是第一个隐含层,Layer1是第四个隐含层。
退化问题:
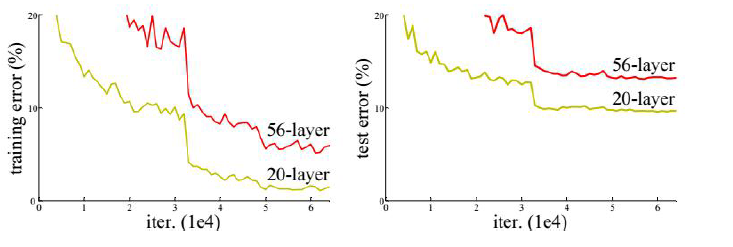
增加网络的层数可以提高网络的精度,但增加到一定程度之后,随着层次的增加,神经网络的训练误差和测
试误差会增大,这个问题称为退化 - 类似维数灾难
退化问题与过拟合不同,过拟合是在测试集上精度差,而退化是在训练集和测试集上精度都下降
改进的总体思路:
改进的目标是网络的精度更高、运行的速度更快。
卷积层
池化层
激活函数
损失函数
网络结构
数据归一化
卷积层的改进:
第一种改进方法是网中网,Network In Network(简称NIN)。普通的卷积是拿一个卷积核去和输入图像进行一个卷积操作,如果不加激活函数操作的话,它是一个线性的操作。而NIN它是用一个小型的神经网络,一般是用多层感知器模型ANN来取代这样一个操作,即用这种非线性的神经网络来代替这样一个卷积,这样效果会更好一些,因为这样它的非线性能力是更强的,当然网络 的复杂度也会升高,虽然是小型的感知器模型,终究还是比算一次卷积要慢一些的。
第二个改进点是Inception机制,这个在讲GoogleNet的时候讲过了,它是把多个不同的尺度的卷积、池化核组合成一个模块来使用,比如说1×1的卷积、3×3的卷积、5×5的卷积、3×3的池化,然后接收前一层的输入,分别进行以上尺寸的卷积池化处理,处理完了以后把它们的结果合并起来,形成输出,这是Inception机制
另外一个要考虑的实际问题是,卷积核的大小设置成多少合适呢。在LeNet-5中使用了5×5的卷积核,AlexNet中用了11×11、5×5等等各种卷积核,前边说了,在VGG出来以后,我们倾向于用小的卷积核,用3×3、1×1的卷积核,这是卷积核的大小。然后卷积核的数量设置成多少合适呢。前边已经说了,一般设置成2的n次方,但是到底设置成128还是256个,是根据你的样本集来定的,如果训练样本集多的话可以把网络搞得复杂一些、卷积核的数量弄得大一些,如果你的训练样本不够的话,网络不能弄得太复杂。
这里再解释一下1×1的卷积,上节课已经提了1×1的卷积但是没有举例子,下面举个例子:
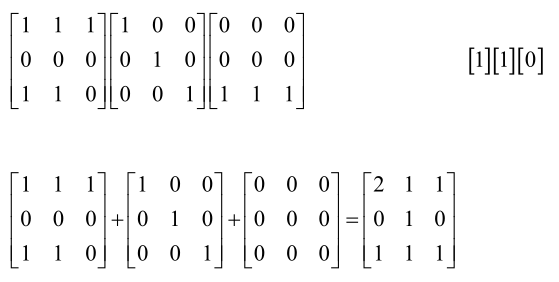
假设我们的输入图像有三个通道,我们的卷积核是1×1的,因此可以把它看成三个标量也可以看成三个1×1的矩阵,那怎么做卷积呢。第一个卷积核作用于第一个通道,用1来乘第一个通道每个位置,可以看到它没有改变图像的高度和宽度w、h,然后拿第二个卷积核和图像的第二个通道卷,拿第三个卷积核和第三个通道卷,卷完以后把三个通道加起来得到最终的输出图像,可以看到,通过这个运算以后,图像的宽度和高度确实是不变的,但是图像的通道数变了,由三个通道变成了一个通道,当然图像的每一层可以用两个通道的卷积核,那最后就会得到两个通道的图像,所以说1×1的卷积不改变图像的高度和宽度,但是会改变图像的通道,相当于在通道上做卷积。
因此我们可以利用1×1这个特性实现全卷积网络以及通道的降维,因为这种卷积可以取代全连接层,这样就可以保证我们的卷积神经网络它接收的输入图像大小是可以变化的,通道降维在GoogleNet里边已经说过了。
再有一种卷积就是反卷积,前边已经说了,反卷积它就是转置卷积,普通卷积我们可以转化成矩阵乘法来实现,y=CX,C是卷积核矩阵,X是卷积图像矩阵,反卷积它可以根据输出图像的尺寸得到输入图像的尺寸,因此它可以实现上采样,因为我们的卷积操作是下采样的把图像尺寸变小了,反卷积可以变回来,因此它可以用来实现全卷积网络。
用矩阵乘法实现卷积