SIGAI机器学习第八集 数据降维1

讲授数据降维原理，PCA的核心思想，计算投影矩阵，投影算法的完整流程，非线性降维技术，流行学习的概念，局部线性嵌入，拉普拉斯特征映射，局部保持投影，等距映射，实际应用

大纲：

数据降维问题
PCA的思想
最佳投影矩阵
向量降维
向量重构
实验环节
实际应用

数据降维问题：

为什么需要数据降维？
①高维数据不易处理，机器学习和模式识别中高维数据不太好处理，如人脸图像32*32,1024维向量，维度太高效率低、影响精度。
②不能可视化，1024维是无法可视化的。
③维数灾难问题，开始增加维度算法预测精度会提升，但再继续增加维度预测精度反而会下降，深层次的原因是在高维空间中样本分布非常稀疏，容易产生过拟合。
④向量各个分量之间可能存在相关性，不利于后边的分析。

数据降维既可以是有监督的学习，也可以是无监督的学习。

数据降维抽象来看跟机器学习算法一样，根据一个输入向量X，预测一个输出向量Y出来，只不过Y的维数比X要低，而且Y尽可能的保持X的信息。

总体上把数据降维分为：

线性降维，映射函数是线性函数

非线性降维，映射函数是非线性函数

PCA的思想：

在线性降维里边最经典的是主成分分析PCA，它基于最小化重构误差的思想。

寻找一个投影矩阵W，左乘X，WX——>Y，将X从高维空间映射到低维空间，但是它保留了高维数据的某些结构信息，使得重构的误差最小化，就是可以根据Y把X重构回来，就像数据压缩算法，压缩完了可以解压缩，解压缩以后要损失比较小。它是怎么做的，它是向数据的主要变化方向投影。

 如图，在黑色斜线垂直方向上数据变化比较小，于是将数据投影到黑色斜线上。如三维空间一个在Z轴方向波动很小的平面，就可以将其投影到XY平面。投影完了以后尽量保留原始数据的信息。

最佳投影矩阵：

投影矩阵W怎么获得，WX——>Y，它的目标是最小化重构误差。

推导分两步：

①把X投影到1维空间

假设有一组样本X₁,X₂,...,X_n，都用同一个向量X₀来代替他，X₀取多少时它的重构误差最小呢，把重构误差定义为均方误差（残差平方和），

求重构误差最小值，对X₀求偏导，

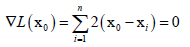
 得到X₀，

，这里m就是X₀。即X₀是所有样本的均值的时候，重构误差是最小的，这也符合我们直观的看法，回归决策树中叶子节点设置为样本的均值时它的误差是最小的。

前边用同一个向量代替所有的向量，这样误差也太大了，因为我们把所有向量的差异都抹杀掉了，强制等于他们所有样本的均值。

现在考虑最简单的情况，比上一个复杂一点，把所有向量投影到一维空间里边去，怎么投影？

，m是所有样本的均值，在均值向量上对每个向量再加上一个a_ie，e是一个单位向量，就像坐标轴一样，把所有样本投影到e坐标轴上去，投影的坐标就是a_i，只要求出a_i和e，就成功把所有样本投影到了一维空间。

定义误差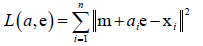：，a_i和e取什么值时误差最小呢？求得误差最小时的a_i和e的值，就是样本要投影的方向及投影的坐标，所有样本投影方向e是同一个方向，而投影坐标a_i是不同样本坐标不同。

求误差最小化分为两步：

先把e当做一个一个常数，看a_i取什么值时误差能够最小化，则求L对a_i的偏导数，令其等于零。

 

这样就解出了a_i，现在只剩下e这个变量，就可以使L最小化，

 

 化简得：

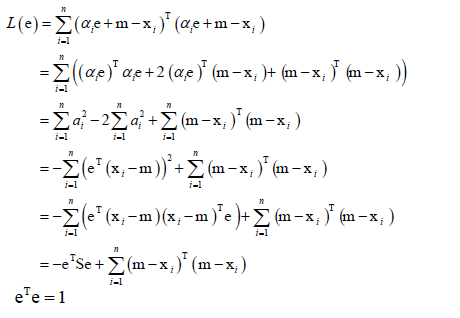
 其中S称为散度矩阵，它是协方差矩阵的n倍，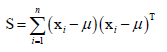

 相当于优化e^TSe最大化，因为L(e)的第二项和e、a_i无关，还有一个约束条件，e^Te=1，因为e是单位向量。于是就转化为求带等式约束的一个二次函数的极值，因为S是二次型（？这点不明白为什么是二次型），展开之后就是二次函数。对于求解带等式约束的极值问题，可以用拉格朗日乘数法来构造拉格朗日乘子函数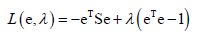，要优化的变量是e和λ，首先对e和λ求偏导数，由于X^TAX对X求偏导的结果为2AX（前提是A是对称矩阵），而X^TX对X求偏导的结果是2X，于是L(e,λ)对e求偏导为-2Se+2λe=0，解方程就可以把e求出来，得到Se=λe，即e是S的特征向量，最优的投影方向e可能就是S的特征向量，特征向量不止一个取哪一个合适呢？

S是一个对称半正定矩阵：

实对称阵一定可以对角化，实对称阵属于不同特征值的特征向量是相互正交的，半正定矩阵能保证它所有的特征值大于等于零，即λ_i≥0，我们取最大特征值对应的特征向量e，因为目标是最大化e^TSe，又e^TSe=λe^Te=λ，即最大值为最大的那个λ，所以e就是最大特征值对应的特征向量。所以主成分分析把向量投影到一维空间里的话，最佳投影方向就是最大特征值对应的那个特征向量，要把特征向量单位化掉。

②把这种做法推广到高维d^'维空间

 前边是把向量投影到一维空间里，把它推广到d^'空间，这里d^'远小于原先向量的维度d，即x∈R^d,d^'<<d。

把向量投影到d^'空间之后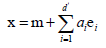，，e_i是正交积（即e_ie_i=1,e_ie_j=0），于是重构误差

优化的目标是最小化误差，化简可得最小化目标是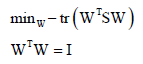，其中W不是方阵，约束条件是让W的行之间相互正交或列之间相互正交。W^TSW，其中S是d×d矩阵，则W^T的尺寸为d^'×d，同样和前边一样的思路最终得到最优解是S对应最大的d^'个特征值对应的特征向量，把这些向量按行（或按列）拼接成一个矩阵，这个矩阵就是最佳投影矩阵W（若按行拼接，则W尺寸为d^'×d），WX就是将向量X从d维降到d^'维向量。

总结：无论将向量投影到一维还是高维，都要求解散度矩阵S的特征值和特征矩阵，在实现的时候一般用协方差矩阵C代替S（C=1/nS）。

 完整的算法流程：

计算投影矩阵的流程：

1.计算所有样本向量的均值向量，并将所有向量减去均值向量，这一步称为白化。
2.计算样本协方差矩阵，cov矩阵。
3.计算协方差矩阵的特征值与特征向量，计算出所有的特征值和特征向量
4.将特征值从大到小排序，保留最大的一部分特征值和特征向量，构成投影矩阵

PCA投影的流程：
1.计算所有样本的均值向量
2.所有样本减掉均值向量，然后再计算协方差矩阵
3.对协方差矩阵进行特征值分解，得到特征值和对应的特征向量
4.将减掉均值后的向量与特征向量矩阵相乘，得到投影结果，即W(X-m)，m是均值向量

还有另外一个过程，叫做向量重构，即已知投影以后的Y求X，则让Y左乘W^T再加上m就得到X。

实验环节：

手写数字样本投影到二维2D：

 手写数字样本投影到三维3D：

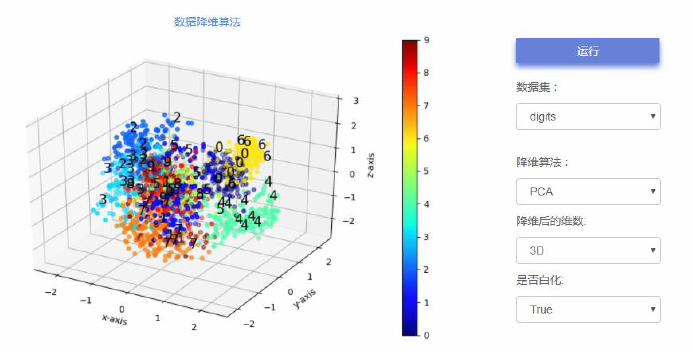
实际应用：

PCA是一个非常通过且古老的算法，在工程和科学的数据分析，包括机器学习、模式识别领域，都得到了大规模的应用，很多时候如果出现向量维数很高的时候，首先想到的就是用PCA给它降维。

比如说在模式识别和机器学习中有几个典型的地方：

人脸识别，特征脸算法，它就是把人脸的图像拼接起来形成一个大的向量然后投影到d维空间里边，然后再用其他算法进行分类，如K近邻、最近邻、支持向量机等。

其他数据降维

PCA计算量还是很大的，如人脸图像32×32拼接起来是1024维的向量，计算协方差矩阵或散度矩阵就是1024×1024的一个矩阵，计算它的特征值和特征向量时的运算量还是很大的。

本集总结：