Largest Rectangle in a Histogram
http://poj.org/problem?id=2559
题意:给出若干宽度相同的矩形的高度(条形统计图),求最大子矩形面积
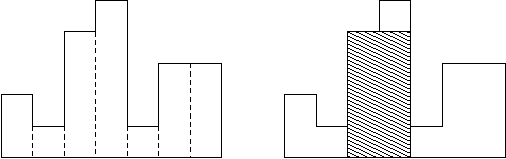
解题思路
单调栈的经典题(嫌弃字多可以先看后面的示例再来看这个思路)
显然,最终的子矩形高度一定和某一个矩形相等(反证)。因此一个暴力的做法就是枚举每一个矩形,然后往两边扩散。在它左侧找到第一个高度比它小的,右侧也一样。则可以求出最大可扩散宽度,乘上高度即可以更新答案。复杂度O(n2)
如果说要优化刚才的算法,也就可以优化寻找最大可扩散宽度的速度
让每一个矩形依次入栈,保存两个关键字:矩形高度,其最大左扩散宽度。保证栈内的矩形高度单调递增
我们可以得到结论:目前栈内的一个矩形uu,在原图中从uu开始一直到栈顶所在的矩形,高度一定都比uu高。这就是为什么我们不需要统计栈内矩形的最大右扩散宽度,因为最大右扩散宽度就是栈顶
再回忆一下最大左扩散宽度的意义,是在它左侧的高度大于它的矩形们。这让我们又得出一个结论:目前栈内的一个矩形uu,如果它的最大左扩散宽度大于11,则这些它所能扩散到的矩形一定都不在栈中。这也很容易发现,因为栈是单调递增的。或者,我们可以得到一个更形象的结论:栈内连续的两个矩形u,vu,v,如果在原图中他们之间有矩形,那么这些矩形一定都高于u,vu,v
因此刚才我们所说的最大左扩散宽度,其实等同于在原图中,它到栈中上一个矩形之间相隔了多少矩形
当一个新的矩形进来的时候,它会弹走若干个矩形。而栈内一个矩形实际上代表着原图中一段矩形。因此可以说是弹走了几段矩形。但是这些被弹走的矩形只不过出栈,在原图中并不会消失。因此他们所代表的的宽度不应当消失,所以我们将他们累积在新进来的这个矩形上。这也非常符合事实——这个新的矩形之所以能弹走这若干个矩形是因为自己比他们矮,因此都可以扩散到。换句话说,被弹走的这一系列矩形最多只能向右扩散到这个新矩形,因此留着它们就没有意义了
而对于任何一个要出栈的矩形,我们需要统计由它的高度所能扩散出去的最大子矩形面积。由于它的最大左扩散宽度已知,唯一需要知道的就是它的最大右扩散宽度。那么由于它在栈里,它的最大右扩散宽度也就是从它一直到最早先的栈顶之间的宽度。因此我们只需要在弹栈的过程中一路累积每个出栈矩形的最大左扩散宽度,加起来就是这一段宽度了。
另外,如果处理完了最后一个矩形以后栈依然有剩余,则应当弹完并更新答案
保证了每个矩形入栈以及出栈恰好一次,在正确性显然的条件下,复杂度O(n)
这里给出示例,以帮助理解:
例子就用题目中的[2,1,5,6,2,3]吧
首先,如果栈是空的,那么索引i入栈。那么第一个i=0就进去吧。注意栈内保存的是索引,不是高度。然后i++。
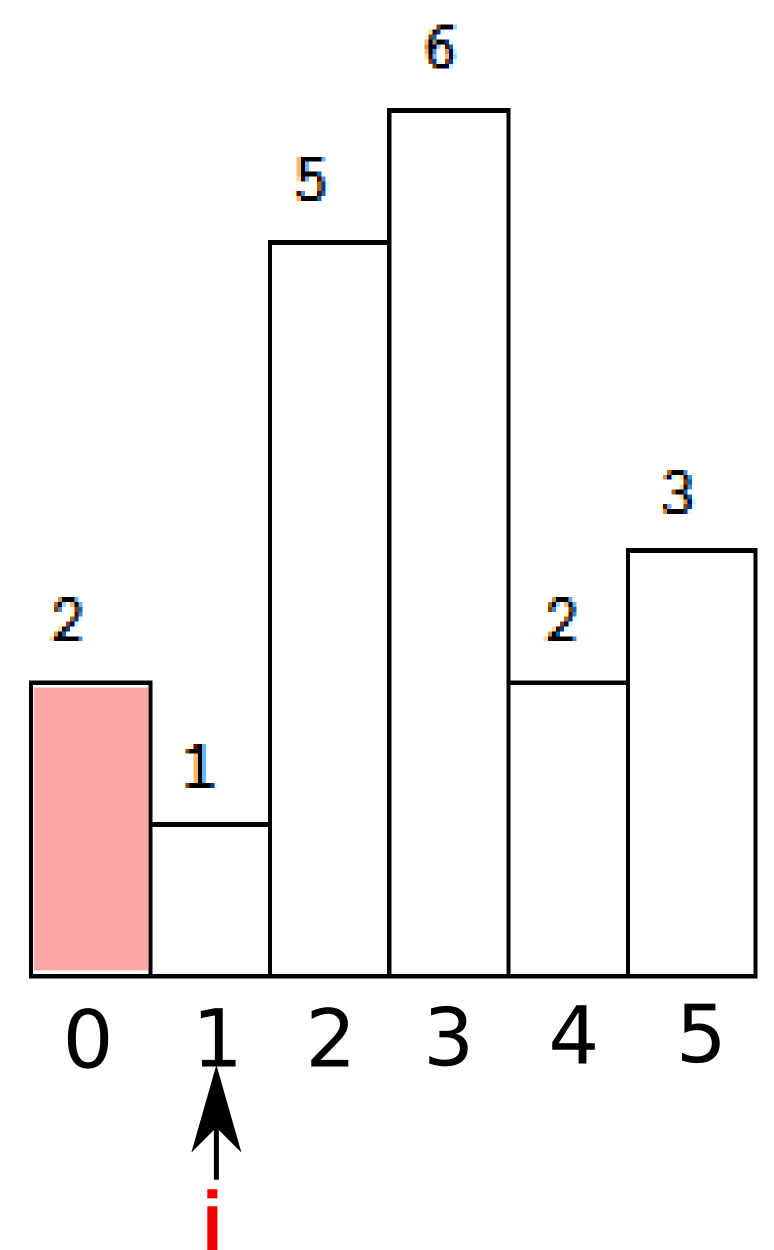
然后继续,当i=1的时候,发现h[i]小于了栈内的元素,于是出栈。(由此可以想到,哦,看来stack里面只存放单调递增的索引)
这时候stack为空,所以面积的计算是h[t] * i.t是刚刚弹出的stack顶元素。也就是蓝色部分的面积。
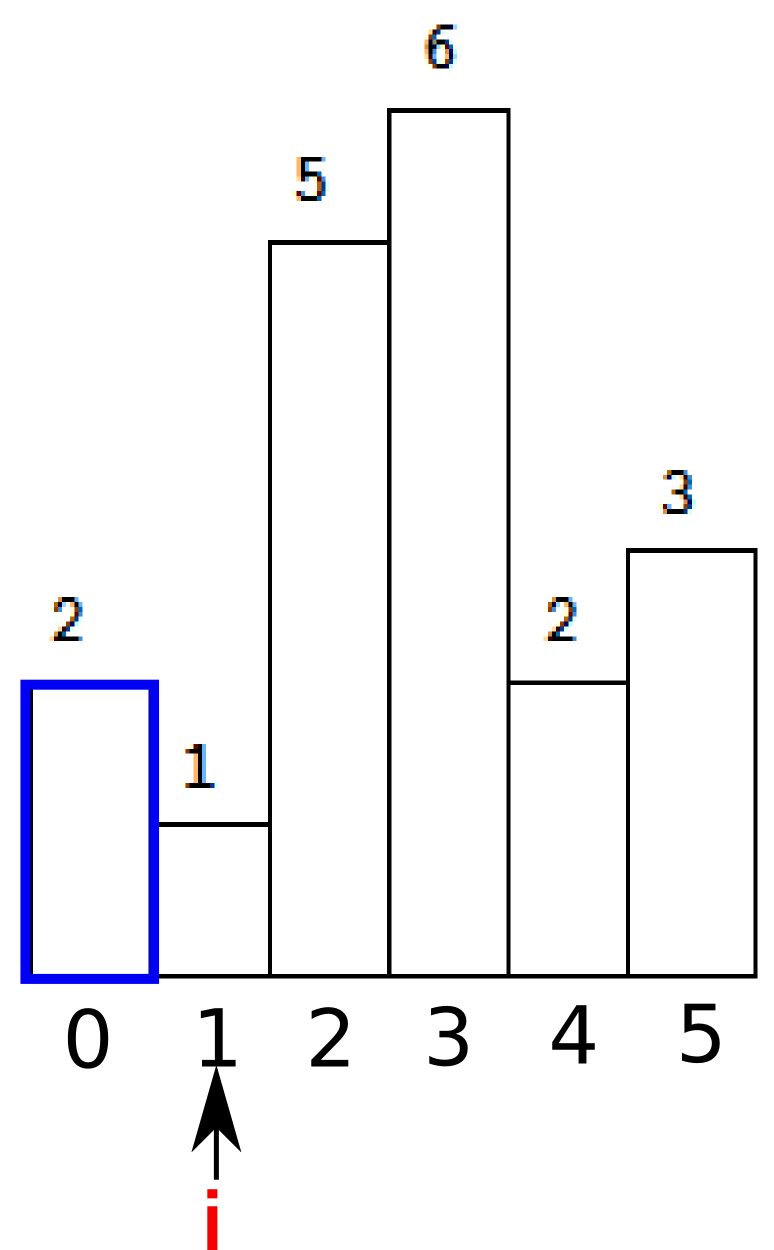
继续。这时候stack为空了,继续入栈。注意到只要是连续递增的序列,我们都要keep pushing,直到我们遇到了i=4,h[i]=2小于了栈顶的元素。
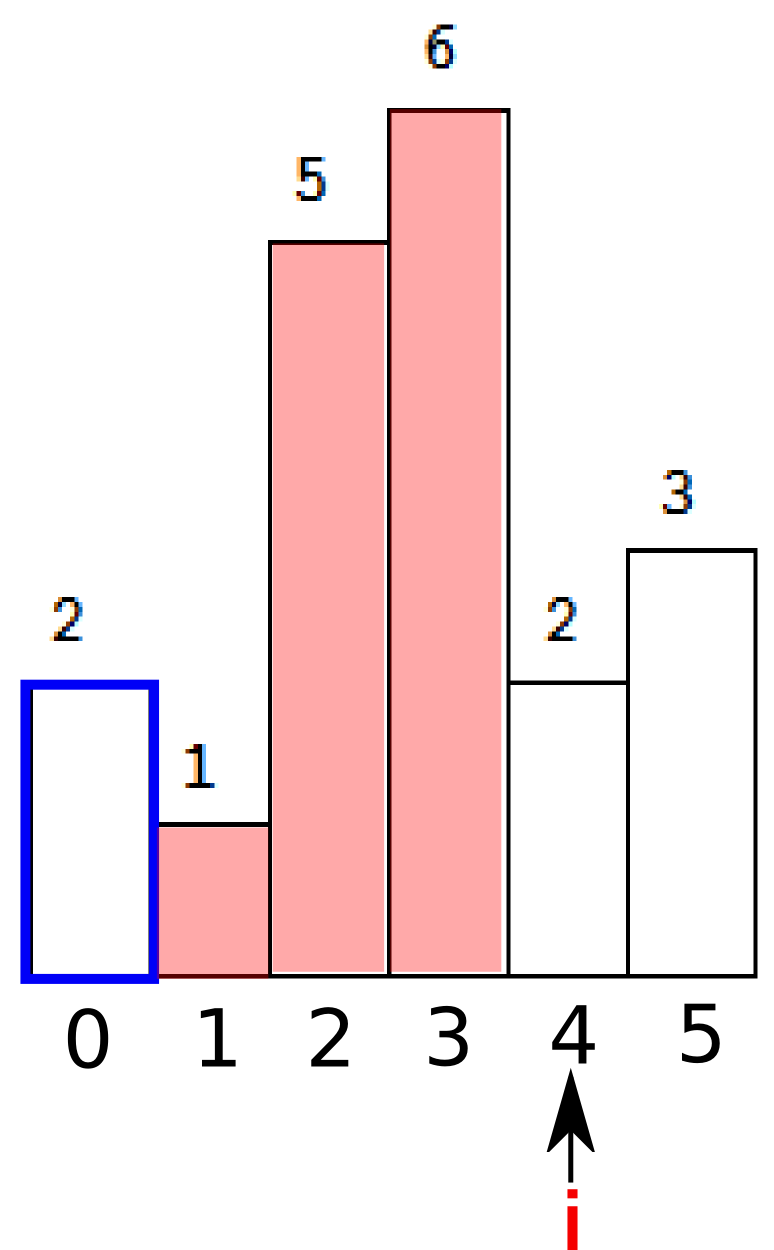
这时候开始计算矩形面积。首先弹出栈顶元素,t=3。即下图绿色部分。
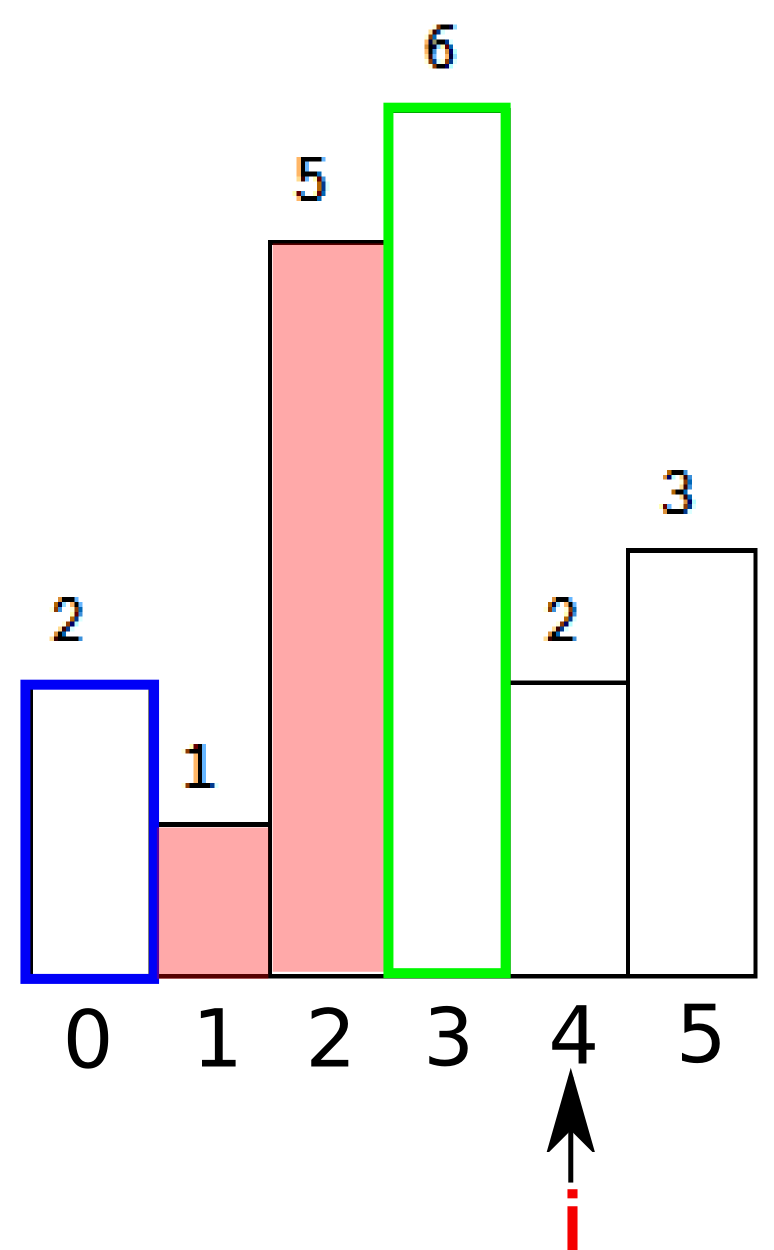
接下来注意到栈顶的(索引指向的)元素还是大于当前i指向的元素,于是出栈,并继续计算面积,桃红色部分。
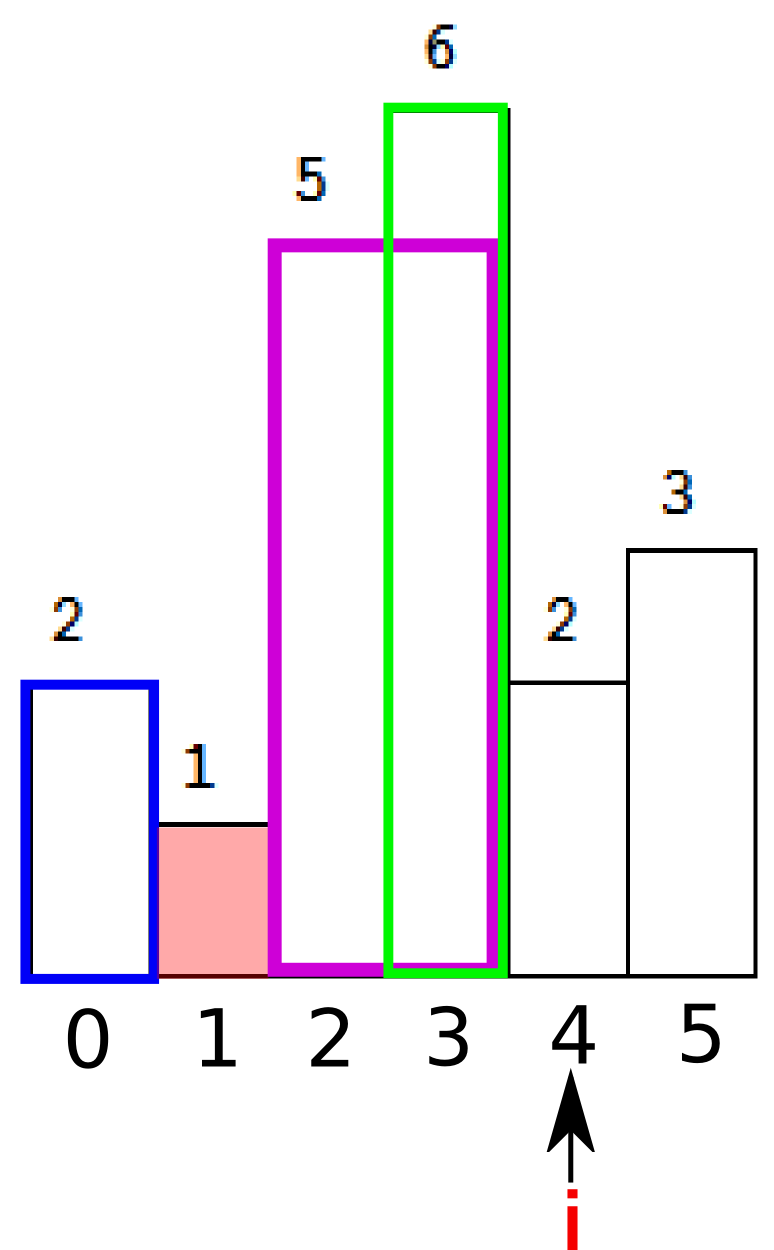
最后,栈顶的(索引指向的)元素大于了当前i指向的元素,循环继续,入栈并推动i前进。直到我们再次遇到下降的元素,也就是我们最后人为添加的dummy元素0.
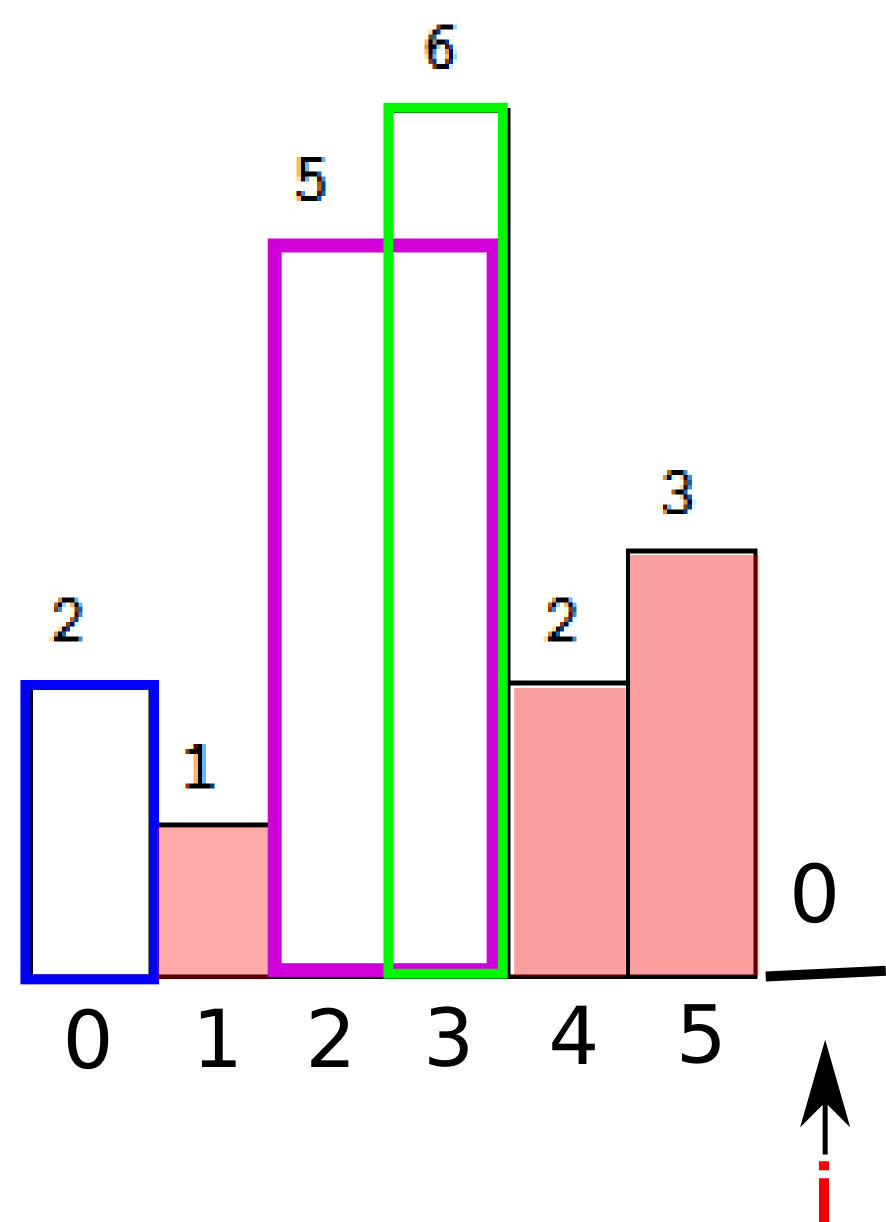
同理,我们计算栈内的面积。由于当前i是最小元素,所以所有的栈内元素都要被弹出并参与面积计算。
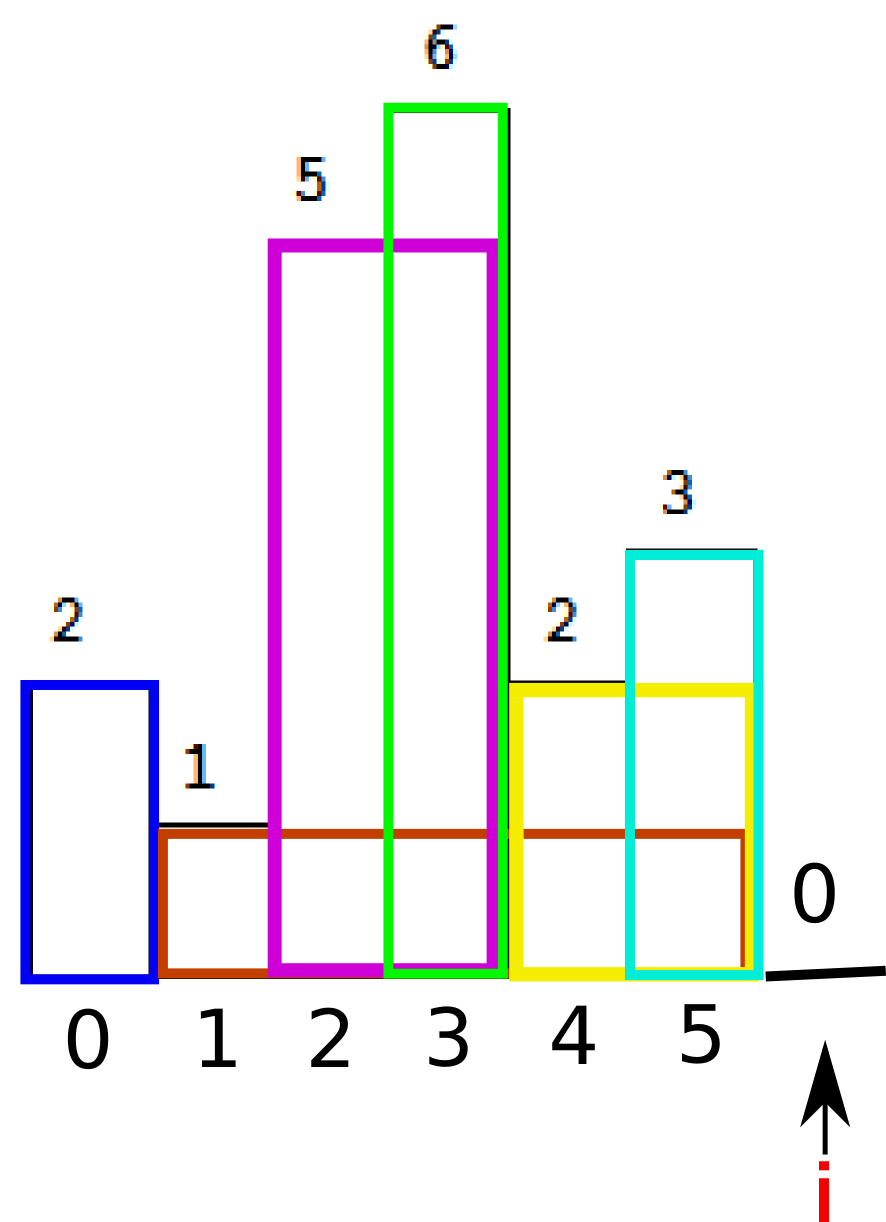
注意我们在计算面积的时候已经更新过了maxArea。
Code
这里如果一下子理解不过来的话,wid可以分两步求,wid = l + r
r = j-t; //右边能扩散的最大宽度 l = s.empty()?t:(t-s.top()-1); //左边能扩大的最大宽度

#include <cstdio> #include <cstring> #include <algorithm> #include <stack> using namespace std; typedef long long ll; ll h[100005]; stack<int> s; int main() { int n; while (scanf("%d", &n)&&n) { memset(h, 0, sizeof(h)); while(!s.empty()) s.pop(); for (int i = 0; i < n; i++) scanf("%lld", &h[i]); ll j = 0, res = 0; while (j<=n) { if (s.empty()||h[s.top()]<=h[j]) s.push(j++); else { ll t = s.top(); s.pop(); ll wid = s.empty()?j:(j-s.top()-1); res = max(res, h[t]*wid); } } printf("%lld ", res); } }
这题算法是没什么问题的,但是特别要注意的是,如何不单独写成一个函数的话,由于最后push进去了h值为0的n,这个对之后wid求值时候可能为负数就会出现问题,还有就是要保证每组数据输入完后h[n]要为0
Largest Submatrix of All 1’s
http://poj.org/problem?id=3494
题意:给你一个n*m的矩阵,矩阵的每个位置值为0或者1,问你在这个矩阵中全部由1组成的最大的矩形面积为多少。
思路:很巧妙的方法。把图拆成一行行来做,分别求以每行为底的最大矩形面积
矩阵中的子矩阵等同于序列中的子序列,只不过此题要做一个预处理,将这个矩阵分为以每一行为x轴的n个柱状图,对于每一个等于1的点,它的高度都等于上一行同一列的点的高度加一。
初始化后,再对n个柱状图进行如上题POJ2559的处理。
例如:






#include<stdio.h> #include<stack> using namespace std; int h[2005][2005]; stack<int> s; int main() { int n, m; while(~scanf("%d%d",&n,&m)) { for(int i = 0; i < n; i++) { for(int j = 0; j < m; j++) { scanf("%d",&h[i][j]); if(h[i][j]==1&&i>0) h[i][j]+=h[i-1][j]; } } for(int i = 0; i < n; i++) h[i][m] = 0; int res = 0; for (int i = 0; i < n; i++) { while(!s.empty()) s.pop(); int j = 0; while (j<=m) { if (s.empty()||h[i][s.top()]<=h[i][j]) s.push(j++); else { int t = s.top(); s.pop(); int wid = s.empty()?j:(j-s.top()-1); res = max(res, h[i][t]*wid); } } } printf("%d ", res); } return 0; }
参考自以下博客:
https://www.cnblogs.com/qixingzhi/p/9497208.html
https://www.cnblogs.com/lichen782/p/leetcode_Largest_Rectangle_in_Histogram.html
