n皇后问题

前言

---

在棋盘上放置8个皇后，使得它们互不攻击，此时每个皇后的攻击范围为同行同列和同对角线，求所有解。

这就是著名的8皇后问题，我们也可以进一步拓展为n皇后问题。这类问题主要是用递归回溯求解，当然也会有各种优化方案，下面就来介绍其中的包含的思想与解法。

解法

---

 经过思考，我们可以发现，假设每行每列放置一个皇后，那么就变成一个排列组和问题。比如我第一行放置皇后时棋盘上的8列都可供选择，那么第二行放置皇后时就只有7列可供选择了，以此类推总共是8! 种。

因此我们从第一行开始，递归搜索所有可能的结果，一旦第8行的皇后能正确放置，此时所有的皇后必不冲突，方案数加一。

void search(int cur){
    if(cur==n) tot++;
    else for(int i = 0; i < n; i++){
        int ok = 1;
        C[cur] = i;
        for(int j = 0; j < cur; j++) //检查是否和前面的皇后冲突 
            if(C[cur]==C[j]||C[cur]-cur==C[j]-j||C[cur]+cur==C[j]+j){
                ok = 0;
                break;
            }
        if(ok) search(cur+1);
    }
} 

ps:我们用下图的方法就能判断皇后是否在同一对角线上面

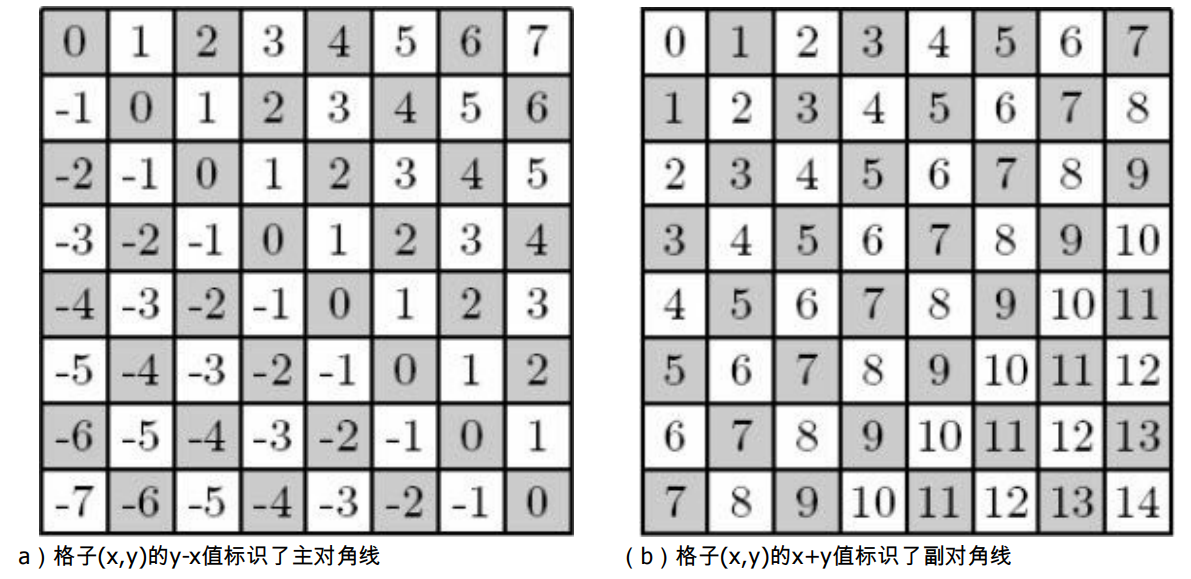
现在解法已然明了，对于一般的递归，我们都是需要优化的，下面来看看两种优化方案：

利用标记

对于某一行来说，我们判断能否放置在哪一列，就是判断这些列或者是他们所在的对角线是某被使用过

因此我们用$vis[0][]$表示使用过的列，$vis[1][]$表示使用过的副对角线，$vis[3][]$表示使用过的主对角线

有个小细节要注意就是由于用$y-x$标记副对角线，可能会出现负数，因此得加上$n$

void search(int cur){
    if(cur==n) tot++;
    else for(int i = 0; i < n; i++){
        if(!vis[0][i]&&!vis[1][cur+i]&&!vis[2][i-cur+n]){
            C[cur] = i;
            vis[0][i] = vis[1][cur+i] = vis[2][i-cur+n] = 1;
            search(cur+1);
            vis[0][i] = vis[1][cur+i] = vis[2][i-cur+n] = 1;//回溯 
        }
    }
} 

利用位运算

同样的思想，只不过我们用位运算来记录这行使用过的列。

                

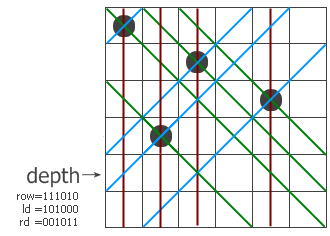
$depth$ 表示当前要进行搜索的层，$row$的二进制表示当前层二进制为1是冲突列，$ld$表示右对角线对当前层造成的冲突列，$rd$表示左对角线对当前层造成的冲突列。

我认为这题使用位运算最神奇的地方，就在于右对角线对下一层造成的冲突列能由$ld<<1$得到，同理左对角线对下一层造成的冲突列能由$rd>>1$得到，而这些你仔细观察上面的图片就能发现。

我们将$row, ld, rd$进行按位或运算就能得到当前行的所有冲突列，然后依次枚举可能的列往下递归即可。

int lowbit(int x){
    return x & -x;
}
void dfs(int row, int ld, int rd){
    if(row==lim){
        ans++;
        return;
    }
    int pos = lim & ~(row|ld|rd);
    while(pos){
        int p = lowbit(pos);
        dfs(row|p, (ld|p)<<1, (rd|p)>>1);
        pos -= p;
    }
}

需要注意的是所有冲突列需要最后与$lim$按位与才能得到正确的结果，因为保存在计算机中的数值是以补码的形式存在，我只需要取低$n$位即可。

比如对于n = 4的情况，取冲突列5 = 00101， ~5 = 11010， 我只需要对~5的低四位1010依次枚举1所在位置即可，如果不取低4位，显然将最左侧的1算进来是错误的。

---

Reference:

https://www.cnblogs.com/tiny656/p/3918367.html

http://www.matrix67.com/blog/archives/266