特征处理是特征工程的核心部分,特征工程是数据分析中最耗时间和精力的一部分工作,它不像算法和模型那样式确定的步骤,更多的是工程上的经验和权衡,因此没有统一的方法,但是sklearn提供了较为完整的特征处理方法,包括数据预处理,特征选择,降维等。首次接触到sklearn,通常会被其丰富且方便的算法模型库吸引,但是这里介绍的特征处理库也非常强大!
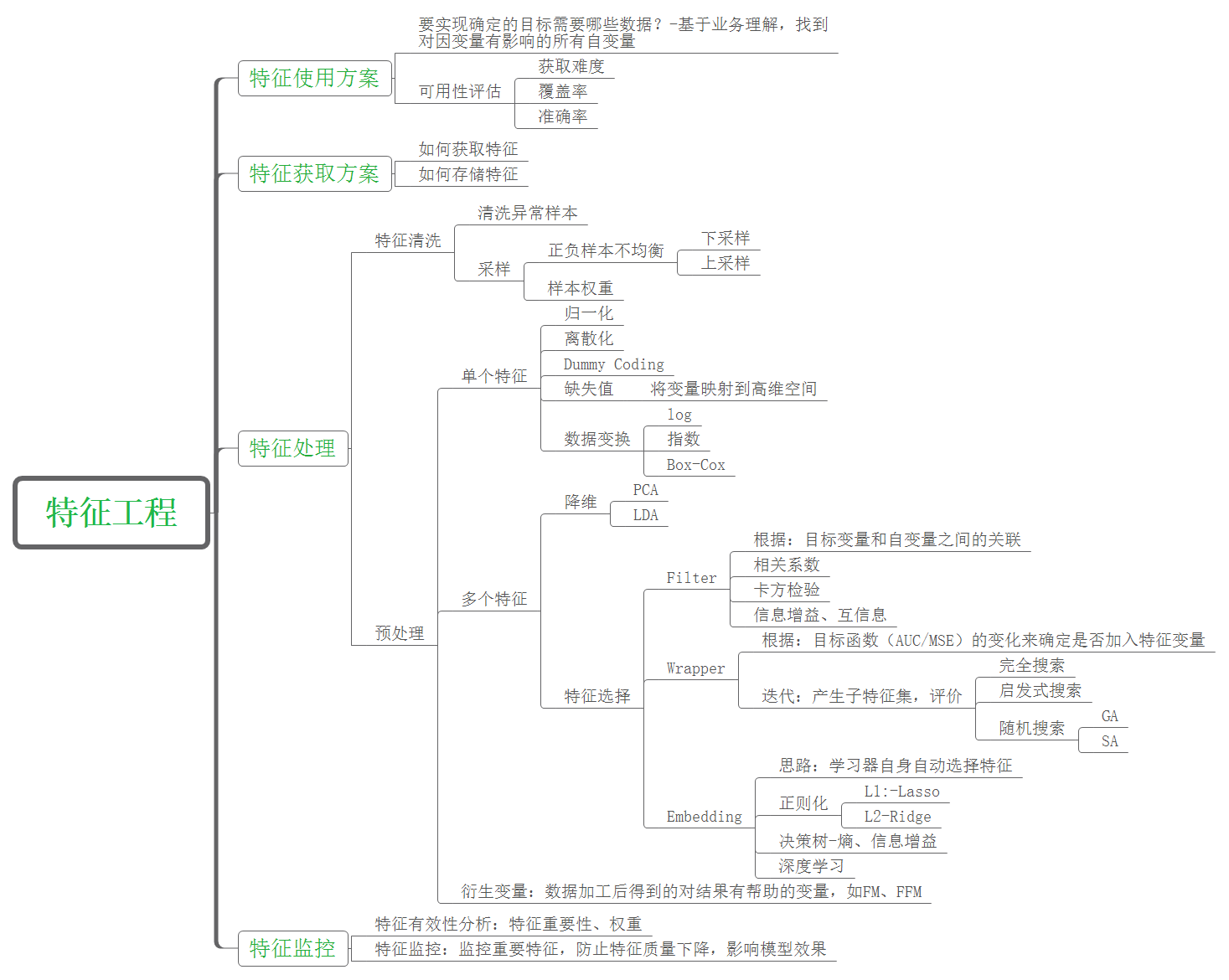
经过前人的总结,特征工程已经形成了接近标准化的流程,如下图所示(此图来自此网友,若侵权,联系我,必删除)
1 特征来源——导入数据
在做数据分析的时候,特征的来源一般有两块,一块是业务已经整理好各种特征数据,我们需要去找出适合我们问题需要的特征;另一块是我们从业务特征中自己去寻找高级数据特征。
本文中使用sklearn中的IRIS(鸢尾花)数据集来对特征处理功能进行说明。IRIS数据集由Fisher在1936年整理,包括4个特征(Sepal.Length(花萼长度)、Sepal.Width(花萼宽度)、Petal.Length(花瓣长度)、Petal.Width(花瓣宽度)),特征值都为正浮点数,单位为厘米,目标值为鸢尾花的分类(Iris Setosa(山鸢尾)、Iris Versicolour(杂色鸢尾),Iris Virginica(维吉尼亚鸢尾))。导入IRIS数据集的代码如下:
from sklearn.datasets import load_iris # 导入IRIS数据集 iris = load_iris() # 特征矩阵 data = iris.data # 目标向量 target = iris.target
从本地导入数据集的代码如下:
# 导入本地的iris数据集
dataframe = pd.read_csv('iris.csv',header=None)
iris_data = dataframe.values
# print(type(iris_data)) #<class 'numpy.ndarray'>
# 特征矩阵
data = iris_data[:,0:-1]
# 目标向量
target = iris_data[:,-1]
其中iris.txt的数据集如下:
5.1,3.5,1.4,0.2,Iris-setosa 4.9,3.0,1.4,0.2,Iris-setosa 4.7,3.2,1.3,0.2,Iris-setosa 4.6,3.1,1.5,0.2,Iris-setosa 5.0,3.6,1.4,0.2,Iris-setosa 5.4,3.9,1.7,0.4,Iris-setosa 4.6,3.4,1.4,0.3,Iris-setosa 5.0,3.4,1.5,0.2,Iris-setosa 4.4,2.9,1.4,0.2,Iris-setosa 4.9,3.1,1.5,0.1,Iris-setosa 5.4,3.7,1.5,0.2,Iris-setosa 4.8,3.4,1.6,0.2,Iris-setosa 4.8,3.0,1.4,0.1,Iris-setosa 4.3,3.0,1.1,0.1,Iris-setosa 5.8,4.0,1.2,0.2,Iris-setosa 5.7,4.4,1.5,0.4,Iris-setosa 5.4,3.9,1.3,0.4,Iris-setosa 5.1,3.5,1.4,0.3,Iris-setosa 5.7,3.8,1.7,0.3,Iris-setosa 5.1,3.8,1.5,0.3,Iris-setosa 5.4,3.4,1.7,0.2,Iris-setosa 5.1,3.7,1.5,0.4,Iris-setosa 4.6,3.6,1.0,0.2,Iris-setosa 5.1,3.3,1.7,0.5,Iris-setosa 4.8,3.4,1.9,0.2,Iris-setosa 5.0,3.0,1.6,0.2,Iris-setosa 5.0,3.4,1.6,0.4,Iris-setosa 5.2,3.5,1.5,0.2,Iris-setosa 5.2,3.4,1.4,0.2,Iris-setosa 4.7,3.2,1.6,0.2,Iris-setosa 4.8,3.1,1.6,0.2,Iris-setosa 5.4,3.4,1.5,0.4,Iris-setosa 5.2,4.1,1.5,0.1,Iris-setosa 5.5,4.2,1.4,0.2,Iris-setosa 4.9,3.1,1.5,0.1,Iris-setosa 5.0,3.2,1.2,0.2,Iris-setosa 5.5,3.5,1.3,0.2,Iris-setosa 4.9,3.1,1.5,0.1,Iris-setosa 4.4,3.0,1.3,0.2,Iris-setosa 5.1,3.4,1.5,0.2,Iris-setosa 5.0,3.5,1.3,0.3,Iris-setosa 4.5,2.3,1.3,0.3,Iris-setosa 4.4,3.2,1.3,0.2,Iris-setosa 5.0,3.5,1.6,0.6,Iris-setosa 5.1,3.8,1.9,0.4,Iris-setosa 4.8,3.0,1.4,0.3,Iris-setosa 5.1,3.8,1.6,0.2,Iris-setosa 4.6,3.2,1.4,0.2,Iris-setosa 5.3,3.7,1.5,0.2,Iris-setosa 5.0,3.3,1.4,0.2,Iris-setosa 7.0,3.2,4.7,1.4,Iris-versicolor 6.4,3.2,4.5,1.5,Iris-versicolor 6.9,3.1,4.9,1.5,Iris-versicolor 5.5,2.3,4.0,1.3,Iris-versicolor 6.5,2.8,4.6,1.5,Iris-versicolor 5.7,2.8,4.5,1.3,Iris-versicolor 6.3,3.3,4.7,1.6,Iris-versicolor 4.9,2.4,3.3,1.0,Iris-versicolor 6.6,2.9,4.6,1.3,Iris-versicolor 5.2,2.7,3.9,1.4,Iris-versicolor 5.0,2.0,3.5,1.0,Iris-versicolor 5.9,3.0,4.2,1.5,Iris-versicolor 6.0,2.2,4.0,1.0,Iris-versicolor 6.1,2.9,4.7,1.4,Iris-versicolor 5.6,2.9,3.6,1.3,Iris-versicolor 6.7,3.1,4.4,1.4,Iris-versicolor 5.6,3.0,4.5,1.5,Iris-versicolor 5.8,2.7,4.1,1.0,Iris-versicolor 6.2,2.2,4.5,1.5,Iris-versicolor 5.6,2.5,3.9,1.1,Iris-versicolor 5.9,3.2,4.8,1.8,Iris-versicolor 6.1,2.8,4.0,1.3,Iris-versicolor 6.3,2.5,4.9,1.5,Iris-versicolor 6.1,2.8,4.7,1.2,Iris-versicolor 6.4,2.9,4.3,1.3,Iris-versicolor 6.6,3.0,4.4,1.4,Iris-versicolor 6.8,2.8,4.8,1.4,Iris-versicolor 6.7,3.0,5.0,1.7,Iris-versicolor 6.0,2.9,4.5,1.5,Iris-versicolor 5.7,2.6,3.5,1.0,Iris-versicolor 5.5,2.4,3.8,1.1,Iris-versicolor 5.5,2.4,3.7,1.0,Iris-versicolor 5.8,2.7,3.9,1.2,Iris-versicolor 6.0,2.7,5.1,1.6,Iris-versicolor 5.4,3.0,4.5,1.5,Iris-versicolor 6.0,3.4,4.5,1.6,Iris-versicolor 6.7,3.1,4.7,1.5,Iris-versicolor 6.3,2.3,4.4,1.3,Iris-versicolor 5.6,3.0,4.1,1.3,Iris-versicolor 5.5,2.5,4.0,1.3,Iris-versicolor 5.5,2.6,4.4,1.2,Iris-versicolor 6.1,3.0,4.6,1.4,Iris-versicolor 5.8,2.6,4.0,1.2,Iris-versicolor 5.0,2.3,3.3,1.0,Iris-versicolor 5.6,2.7,4.2,1.3,Iris-versicolor 5.7,3.0,4.2,1.2,Iris-versicolor 5.7,2.9,4.2,1.3,Iris-versicolor 6.2,2.9,4.3,1.3,Iris-versicolor 5.1,2.5,3.0,1.1,Iris-versicolor 5.7,2.8,4.1,1.3,Iris-versicolor 6.3,3.3,6.0,2.5,Iris-virginica 5.8,2.7,5.1,1.9,Iris-virginica 7.1,3.0,5.9,2.1,Iris-virginica 6.3,2.9,5.6,1.8,Iris-virginica 6.5,3.0,5.8,2.2,Iris-virginica 7.6,3.0,6.6,2.1,Iris-virginica 4.9,2.5,4.5,1.7,Iris-virginica 7.3,2.9,6.3,1.8,Iris-virginica 6.7,2.5,5.8,1.8,Iris-virginica 7.2,3.6,6.1,2.5,Iris-virginica 6.5,3.2,5.1,2.0,Iris-virginica 6.4,2.7,5.3,1.9,Iris-virginica 6.8,3.0,5.5,2.1,Iris-virginica 5.7,2.5,5.0,2.0,Iris-virginica 5.8,2.8,5.1,2.4,Iris-virginica 6.4,3.2,5.3,2.3,Iris-virginica 6.5,3.0,5.5,1.8,Iris-virginica 7.7,3.8,6.7,2.2,Iris-virginica 7.7,2.6,6.9,2.3,Iris-virginica 6.0,2.2,5.0,1.5,Iris-virginica 6.9,3.2,5.7,2.3,Iris-virginica 5.6,2.8,4.9,2.0,Iris-virginica 7.7,2.8,6.7,2.0,Iris-virginica 6.3,2.7,4.9,1.8,Iris-virginica 6.7,3.3,5.7,2.1,Iris-virginica 7.2,3.2,6.0,1.8,Iris-virginica 6.2,2.8,4.8,1.8,Iris-virginica 6.1,3.0,4.9,1.8,Iris-virginica 6.4,2.8,5.6,2.1,Iris-virginica 7.2,3.0,5.8,1.6,Iris-virginica 7.4,2.8,6.1,1.9,Iris-virginica 7.9,3.8,6.4,2.0,Iris-virginica 6.4,2.8,5.6,2.2,Iris-virginica 6.3,2.8,5.1,1.5,Iris-virginica 6.1,2.6,5.6,1.4,Iris-virginica 7.7,3.0,6.1,2.3,Iris-virginica 6.3,3.4,5.6,2.4,Iris-virginica 6.4,3.1,5.5,1.8,Iris-virginica 6.0,3.0,4.8,1.8,Iris-virginica 6.9,3.1,5.4,2.1,Iris-virginica 6.7,3.1,5.6,2.4,Iris-virginica 6.9,3.1,5.1,2.3,Iris-virginica 5.8,2.7,5.1,1.9,Iris-virginica 6.8,3.2,5.9,2.3,Iris-virginica 6.7,3.3,5.7,2.5,Iris-virginica 6.7,3.0,5.2,2.3,Iris-virginica 6.3,2.5,5.0,1.9,Iris-virginica 6.5,3.0,5.2,2.0,Iris-virginica 6.2,3.4,5.4,2.3,Iris-virginica 5.9,3.0,5.1,1.8,Iris-virginica
2,数据预处理
对于一个项目,首先是分析项目的目的和需求,了解这个项目属于什么问题,要达到什么效果。然后提取数据,做基本的数据清洗。第三步是特征工程,这个需要耗费很大的精力。如果特征工程做得好,那么后面选择什么算法其实差异不大,反之,不管选择什么算法,效果都不会有突破性的提升。第四步是跑算法,通常情况下,我将自己会的所有的能跑的算法先跑一遍,看看效果,分析一下precesion/recall和f1-score,看看有没有什么异常(譬如有好几个算法precision特别好,但是recall特别低,这就要从数据中找原因,或者从算法中看是不是因为算法不适合这个数据),如果没有异常,那么就进行下一步,选择一两个跑的结果最好的算法进行调优。调优的方法很多,调整参数的话可以用网格搜索,随机搜索等,调整性能的话,可以根据具体的数据和场景进行具体分析,调优后再去跑一遍算法,看有没有提高,如果没有,找原因,数据还是算法问题,是数据质量不好,还是特征问题,还是算法问题??一个一个排查,找解决方法,特征问题就回到第三步再进行特征工程,数据问题就回到第一步看数据清洗有没有遗漏,异常值是否影响了算法的结果,算法问题就回到第四步,看算法流程中哪一步出了问题。如果实在不行,可以搜一下相关的论文,看看论文中有没有解决方法。这样反复来几遍,就可以出结果了,写技术文档和分析报告,最后想产品讲解我们做的东西。然后他们再提需求,不断循环,最后代码上线,该bug。
直观来看,可以使用一个流程图来表示:

为什么要进行数据清洗呢?
我们之前实践的数据,比如iris数据集,波士顿房价数据,电影评分数据集,手写数字数据集等等,数据质量都很高,没有缺失值,没有异常点,也没有噪音。而在真实数据中,我们拿到的数据可能包含了大量的缺失值,可能包含大量的噪音,也可能因为人工录入错误导致有异常点存在,对我们挖掘出有效信息造成了一定的困扰,所以我们需要通过一些方法啊,尽量提高数据的质量。
2.1,分析数据
在实际项目中,当我们确定需求后就会去找相应的数据,拿到数据后,首先要对数据进行描述性统计分析,查看哪些数据是不合理的,也可以知道数据的基本情况。如果是销售额数据可以通过分析不同商品的销售总额,人均消费额,人均消费次数等,同一商品的不同时间的消费额,消费频次等等,了解数据的基本情况。此外可以通过作图的形式来了解数据的质量,有无异常点,有无噪音等。
python中包含了大量的统计命令,其中主要的统计特征函数如下图所示:
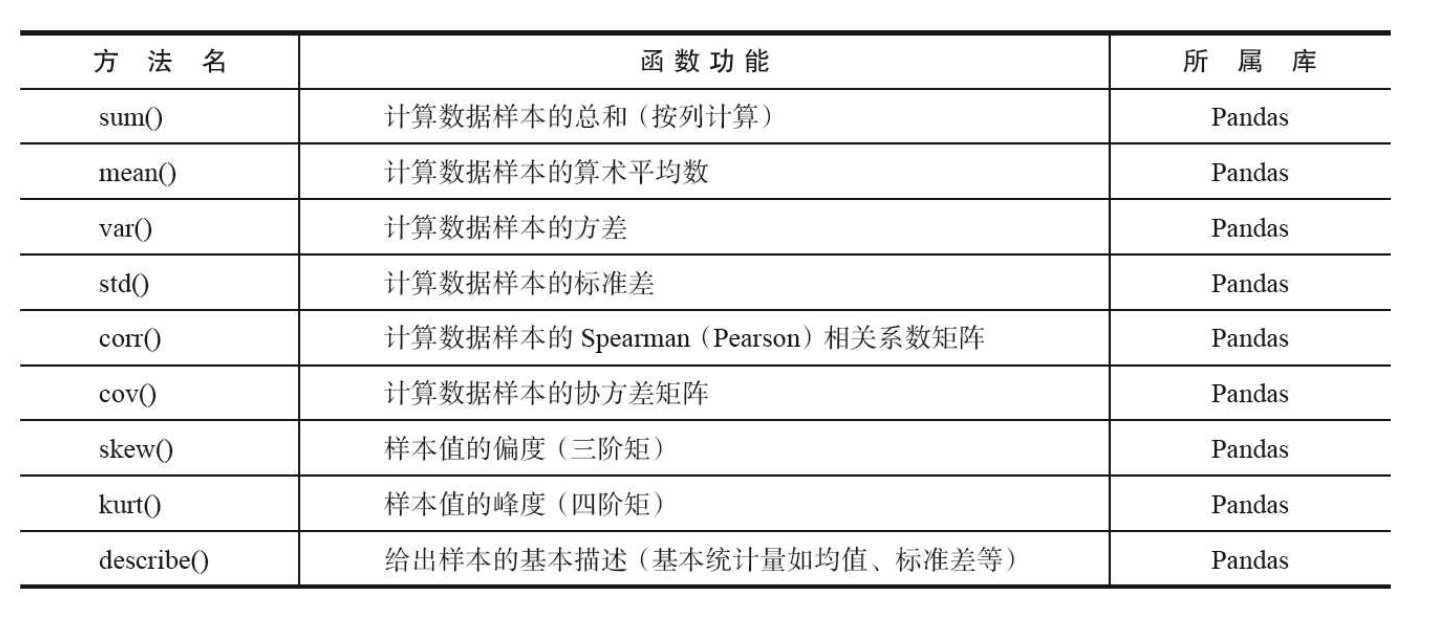
2.2 处理数据(无量纲化数据的处理)
通过特征提取,我们能得到未经处理的特征,这时的特征可能有以下问题:
- 1,不属于同一量纲:即特征的规格不一样,不能放在一起比较。无量纲化可以解决这一问题。
- 2,信息亢余:对于某些定量特征,其包含的有效信息为区间划分,例如学习成绩,假若只关心“及格”或者“不及格”,那么需要将定量的考分,转换成“1”和“0”表示及格和不及格。二值化可以解决这一问题。
- 3,定性特征不能直接使用:某些机器学习算法和模型只能接受定量特征的输入,那么需要将定性特征转换为定量特征。最简单的方式是为每一种定性值指定一个定量值,但是这种方式过于灵活,增加了调参的工作。通常使用哑编码的方式将定性特征转化为定量特征:假设有N种定性值,则将这一个特征扩展为N种特征,当原始特征值为第i种定性值时,第i个扩展特征赋值为1,其他扩展特征赋值为0,哑编码的方式相比直接指定的方式,不用增加调参的工作,对于线性模型来说,使用哑编码后的特征可达到非线性的效果
- 4,存在缺失值:缺失值需要补充
- 5,信息利用率低:不同的机器学习算法和模型对数据中信息的利用是不同的,之前提到在线性模型中,使用对定性特征哑编码可以达到非线性的效果。类似的,对于定量变量多项式化,或者进行其他的转换,都能达到非线性的效果。
我们使用sklearn中的preprocessing库来进行数据预处理,可以覆盖以上问题的解决方案。
无量纲化使不同规格的数据转换到同一规则。常见的无量纲化方法有标准化和区间缩放法。标准化的前提是特征值服从正态分布,标准化后,其转换成标准正态分布。区间缩放法利用了边界值信息,将特征的取值区间缩放到某个特点的范围,例如[0,1]等。
2.2.1 标准化
标准化需要计算特征的均值和标准差,公式表达为:
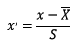
使用preprocessing库的StandardScaler类对数据进行标准化的代码如下:
from sklearn.preprocessing import StandardScaler #标准化,返回值为标准化后的数据 StandardScaler().fit_transform(iris.data)
StandardScler计算训练集的平均值和标准差,以便测试数据及使用相同的变换,变换后的各维特征有0均值,单位方差(也叫z-score规范化),计算方式是将特征值减去均值,除以标准差。
fit 用于计算训练数据的均值和方差,后面就会使用均值和方差来转换训练数据
fit_transform 不仅计算训练数据的均值和方差,还会用计算出来的均值和方差来转换训练数据,从而把数据转化成标准的正态分布。
transform 很显然,这只是进行转换,只是把训练数据转换成标准的正态分布。
为什么要标准化?
通常情况下是为了消除量纲的影响。譬如一个百分制的变量与一个5分值的变量在一起怎么比较呢?只有通过数据标准化,都把他们标准到同一个标准时才具有可比性,一般标准化采用的是Z标准化,即均值为0,方差为1,当然也有其他标准化,比如0-1 标准化等等,可根据自己的数据分布情况和模型来选择。
标准化适用情况
看模型是否具有伸缩不变性。
不是所有的模型都一定需要标准化,有些模型对量纲不同的数据比较敏感,譬如SVM等。当各个维度进行不均匀伸缩后,最优解与原来不等价,这样的模型,除非原始数据的分布范围本来就不叫接近,否则必须进行标准化,以免模型参数被分布范围较大或较小的数据主导。但是如果模型在各个维度进行不均匀伸缩后,最优解与原来等价,例如logistic regression等,对于这样的模型,是否标准化理论上不会改变最优解。但是,由于实际求解往往使用迭代算法,如果目标函数的形状太“扁”,迭代算法可能收敛地很慢甚至不收敛,所以对于具有伸缩不变性的模型,最好也进行数据标准化。
2.2.2 区间缩放法(最小-最大规范化)
区间缩放法的思路有很多,常见的一种为利用两个极值进行缩放,公式表达为:
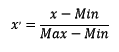
使用preproccessing库的MinMaxScaler类对数据进行区间缩放的代码如下:
from sklearn.preprocessing import MinMaxScaler #区间缩放,返回值为缩放到[0, 1]区间的数据 MinMaxScaler().fit_transform(iris.data)
区间缩放是对原始数据进行线性变换,变换到[0,1] 区间(当然也可以是其他固定最小最大值的区间)
2.2.3 正则化(normalize)
机器学习中,如果参数过多,模型过于复杂,容易造成过拟合(overfit)。即模型在训练样本数据上表现的很好,但在实际测试样本上表现的较差,不具有良好的泛化能力,为了避免过拟合,最常用的一种方法是使用正则化,例如L1和L2正则化。
正则化的思想是:首先求出样本的P范数,然后该样本的所有元素都要除以该范数,这样使得最终每个样本的范数都是1,规范化(Normalization)是将不同变化范围的值映射到相同的固定范围,常见的是[0,1],也称为归一化。
如下例子,将每个样本变换成unit norm。
x=np.array([[1.,-1.,2.],
[2.,0.,0.],
[0.,1.,-1.]])
x_normalized=preprocessing.normalize(x,norm='l2')
print(x_normalized)
# 可以使用processing.Normalizer()类实现对训练集和测试集的拟合和转换
normalizer=preprocessing.Normalizer().fit(x)
print(normalizer)
normalizer.transform(x)
2.3 对定量特征二值化
定量特征二值化的核心在于设定一个阈值,大于阈值的赋值为1,小于等于阈值的赋值为0,公式如下:
![]()
使用preprocessing库的Binarizer类对数据进行二值化的代码如下:
from sklearn.preprocessing import Binarizer #二值化,阈值设置为3,返回值为二值化后的数据 Binarizer(threshold=3).fit_transform(iris.data)
给定阈值,将特征转化为0/1,最主要的是确定阈值设置。
2.4 对定性特征哑编码
由于IRIS数据集的特征皆为定量特征,故使用其目标值进行哑编码(实际上是不需要的)。使用preprocessing库的OneHotEncoder类对数据进行哑编码的代码如下:
from sklearn.preprocessing import OneHotEncoder #哑编码,对IRIS数据集的目标值,返回值为哑编码后的数据 OneHotEncoder().fit_transform(iris.target.reshape((-1,1)))
One-hot编码是使一种对离散特征值的编码方式,在LR模型中常用到,用于给线性模型增加非线性能力。
2.5 缺失值计算
缺失值是指粗糙数据中由于缺少信息而造成的数据的聚类,分组,删除或者截断。它指的是现有数据集中某个或者某些属性的值时不完全的。
缺失值在实际数据中是不可避免的问题,有的人看到缺失值就直接删除了,有的人直接赋予0值或者某一个特殊的值,那么到底该如何处理呢?对于不同的数据场景应该采取不同的策略,首先应该判断缺失值的分布情况。
当缺失值如果占了95%以上,可以直接去掉这个维度的数据,直接删除会对后面的算法跑的结果造成不好的影响,我们常用的方法如下:
2.5.1 删除缺失值
如果一个样本或者变量中所包含的缺失值超过一定的比例,比如超过样本或者变量的一半,此时这个样本或者变量所含有的信息是有限的,如果我们强行对数据进行填充处理,可能会加入过大的人工信息,导致建模效果大打折扣,这种情况下,我们一般选择从数据中剔除整个样本或者变量,即删除缺失值。
2.5.2 缺失值填充
-
随机填充法
从字面上理解就是找一个随机数,对缺失值进行填充,这种方法没有考虑任何的数据特性,填充后可能还是会出现异常值等情况。譬如将缺失值使用“Unknown”等填充,但是效果不一定好,因为算法可能会把他识别称为一个新的类别。一般情况下不建议使用。
-
均值填充法
寻找与缺失值变量相关性最大的那个变量把数据分成几个组,然后分别计算每个组的均值,然后把均值填入缺失的位置作为它的值,如果找不到相关性较好的变量,也可以统计变量已有数据的均值,然后把它填入缺失位置。这种方法会在一定程度上改变数据的分布。
trainData['total_acc'].fillna(trainData['total_acc'].mean(), inplace=True)
-
最相似填充法
在数据集中找到一个与它最相似的样本,然后用这个样本的值对缺失值进行填充。
与均值填充法有点类似,寻找与缺失值变量(比如x)相关性最大的那个变量(比如y),然后按照变量y的值进行排序,然后得到相应的x的排序,最后用缺失值所在位置的前一个值来代替缺失值。
-
回归填充法(建模法)
把缺失值变量作为一个目标变量y,把缺失值变量已有部分数据作为训练集,寻找与其高度相关的变量x建立回归方程,然后把缺失值变量y所在位置对应的x作为预测集,对缺失进行预测,用预测结果来代替缺失值。
可以用回归,使用贝叶斯形式方法的基于推理的工具或者决策树归纳确定。例如利用数据集中其他数据的属性,可以构造一棵判断树,来预测缺失值的值。
-
k近邻填充法
利用knn算法,选择缺失值的最近k个近邻点,然后根据缺失值所在的点离这几个点距离的远近进行加权平均来估计缺失值。
-
多重插补法
通过变量之间的关系对缺失数据进行预测,利用蒙特卡洛方法生成多个完整的数据集,在对这些数据集进行分析,最后对分析结果进行汇总处理
-
中位数填充法
trainData['total_acc'].fillna(trainData['total_acc'].median(), inplace=True)
2.5.3 示例——均值填充法
由于IRIS数据集没有缺失值,故对数据集新增一个样本,4个特征均赋值为NaN,表示数据缺失。使用preprocessing库的Imputer类对数据进行缺失值计算的代码如下:
from numpy import vstack, array, nan from sklearn.preprocessing import Imputer #缺失值计算,返回值为计算缺失值后的数据 #参数missing_value为缺失值的表示形式,默认为NaN #参数strategy为缺失值填充方式,默认为mean(均值) Imputer().fit_transform(vstack((array([nan, nan, nan, nan]), iris.data)))
2.5.4 Imputer() 处理丢失值
各属性必须是数值。
from sklearn.preprocessing import Imputer
# 指定用何值替换丢失的值,此处为中位数
imputer = Imputer(strategy="median")
# 使实例适应数据
imputer.fit(housing_num)
# 结果在statistics_ 变量中
imputer.statistics_
# 替换
X = imputer.transform(housing_num)
housing_tr = pd.DataFrame(X, columns=housing_num.columns,
index = list(housing.index.values))
# 预览
housing_tr.loc[sample_incomplete_rows.index.values]
2.6 数据变换
常用的数据变换有基于多项式的,基于指数函数的,基于对数函数的,4个特征,度为2的多项式转换公式如下:
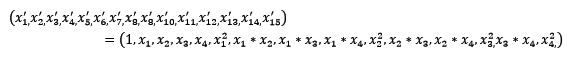
使用preprocessing库的PolynomialFeatures类对数据进行多项式转换的代码如下:
from sklearn.preprocessing import PolynomialFeatures #多项式转换 #参数degree为度,默认值为2 PolynomialFeatures().fit_transform(iris.data)
基于单变元函数的数据变换可以使用一个统一的方式完成,使用preprocessing库的FunctionTransformer 对数据进行对数函数转换的代码如下:
from numpy import log1p from sklearn.preprocessing import FunctionTransformer #自定义转换函数为对数函数的数据变换 #第一个参数是单变元函数 FunctionTransformer(log1p).fit_transform(iris.data)
2.7 异常值处理
异常值我们通常也称为“离群点”,我们在实际项目中拿到的数据往往有不少异常数据,有时候不筛选出这些异常数据很可能让我们后面的数据分析模型有很大的偏差。所以我们应该如何筛选出异常特征样本呢?
-
简单的统计分析
拿到数据可以对数据进行一个简单的描述性统计分析,譬如最大值最小值可以用来判断这个变量的取值是否超过了合理的范围,如客户的年龄为-20岁或者125岁,显然是不合理的,为异常值。
在python中可以直接使用pandas的describe():
>>> import pandas as pd
>>> data = pd.read_table("test.tsv",header = None)
>>> data.describe()
0 1
count 743.000000 735.000000
mean 372.000000 1962.165986
std 214.629914 860.720997
min 1.000000 472.000000
25% 186.500000 1391.000000
50% 372.000000 1764.000000
75% 557.500000 2217.500000
max 743.000000 5906.000000
-
截断法
数据预处理第一步,通常是对异常值的处理。“截断”方法具体步骤为:首先,求一次过程中原始数据的上四分位值Q3,作为首尾无效数据限界点;然后从原始数据的开头向后和尾部向前,提出所有小于Q3数值,直到碰到第一个不小于Q3的数据,则停止截断。
首先,要得到数据的上四分位数和下四分位数,利用np.percentile(),用法如下:

import numpy as np x = np.array([[1,2,3],[7,8,9]]) Q1 = np.percentile(x,25) # 1st quartile Q3 = np.percentile(x,75) # 3st quartile
可能正确的代码如下:
def data_process(data):
# 百分位数是统计中使用的度量 表示小于这个值的观察值占某个百分比 q 要计算的百分位数,在 0 ~ 100 之间
a = np.percentile(data, 75)
i = 0
j = len(data) - 1
while data[i] < a or data[j] < a:
if data[i] < a:
i += 1
if data[j] < a:
j -= 1
if i == j:
break
return data[i:j + 1]
def clean(data):
q3 = np.percentile(data,75)
q1 = np.percentile(data,25)
up = q3 + 1.5 * (q3 - q1)
down = q1 - 1.5 * (q3 - q1)
data = data[(data < up) & (data > down)]
return data
假设数据集时x = [1,2,3,98,99,10000],显然最后一个数10000是一个超限点,它的Q1 = 25,Q3 = 75,四分位距IQR(the interquartile range)=Q1 - Q3。若上下界分别扩大0.5倍,令k = 1.5 为high = Q3 + k*(Q3-Q1),下界为low = Q1-k*(Q3-Q1),即上界为-50下界为150,显然10000超限,如果想调整上界下界的范围,调整系数即可。
四分位数(Quartile)是统计学中分位数的一种,即把全部数值由小到大排列并分成四等份。 处于三个切割点位置的数值就是四分位数。 第一四分位数 (Q1)。又称“较小四分位数”,等于该样本中全部数值由小到大排列后第25%的数字。 第二四分位数 (Q2)。又称“中位数”,等于该样本中全部数值由小到大排列后第50%的数字。 第三四分位数 (Q3),又称“较大四分位数”,等于该样本中全部数值由小到大排列后第75%的数字。 第三四分位数与第一四分位数的差距又称四分位距(InterQuartile Range, IQR)
对于一个矩阵df,按列循环找到每列数据的异常值,如果某个样本含有n个以上的超限特征,返回行号。
注意:在进行这一步之前,先要处理好缺失值的标签量。
# outlier detection
def detect_outliers(df,n,feature_name):
'''
df: the feature dataframe;
n: if outlier feature more than n
features: the name of columns detected
return the index
'''
outlier_indices=[]
for col in feature_name:
Q1 = np.percentile(df[col],25)
Q3 = np.percentile(df[col],75)
# interquartile range(IQR)
IQR = Q3 - Q1
outlier_step = 1.5 * IQR
# Determine a list of indeices of ouliers for feature col
outlier_list_col = df[(df[col] < Q1 - outlier_step) | (df[col] > Q3 + outlier_step)].index.tolist()
# append the found oulier indices for col to the list of outlier indices
outlier_indices.extend(outlier_list_col)
# select observations containing more than 2 outliers
outlier_indices = Counter(outlier_indices)
multiple_outliers = list(k for k, v in outlier_indices.items() if v > n)
return multiple_outliers
经过检查后,假设特征矩阵有10(列)个特征,规范包含大于4列超过了范围,返回行号。
ouliter_result = detect_outliers(feature, 4, feature.columns.tolist())
-
单变量异常值检测(格拉布斯法)
首先,将变量按照其值从小到大进行顺序排列x1,x2.....xn
其次,计算平均值x拔和标准差S,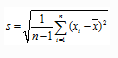
同时计算偏离值,即平均值与最大值之差和平均值与最小值之差,然后确定一个可疑值,一般是偏离平均值较大的那个。
计算统计量gi(残差与标准差的比值),i为可疑值的序列号。
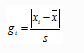
再者,将gi与格拉布斯表给出的临界值GP(n)比较,如果计算的Gi值大于表中的临界值GP(n),则能判断该测量数据是异常值,可以剔除。这里临界值GP(n)与两个参数有关:检出水平α和测量次数n 。
检出水平α:如果要求严格,检出水平α可以定得小一些,例如定α=0.01,那么置信概率P=1-α=0.99;如果要求不严格,α可以定得大一些,例如定α=0.10,即P=0.90;通常定α=0.05,P=0.95。
-
多变量异常值检测(基于距离计算)
基于距离的多变量异常值检测类似与k近邻算法的思路,一般的思路是计算各样本点到中心点的距离,如果距离太大,则判断为异常值,这里距离的度量一般使用马氏距离(Mahalanobis Distance)。因为马氏距离不受量纲的影响,而且在多元条件下,马氏距离还考虑了变量之间的相关性,这使得它优于欧氏距离。
-
异常点检测方法
主要是使用IForest 或者One Class SVM ,使用异常点检测的机器学习算法来过滤所有的异常点。
-
3∂原则
-
箱型图分析
-
基于模型检测
-
基于距离
-
基于密度
-
基于聚类
2.8 处理不平衡数据
我们做分类算法训练时,如果训练集里的各个类别的样本数量不是大约相同的比例,就需要处理样本不平衡问题,也许你会说,不处理会怎么样呢?如果不处理,那么拟合出来的模型对于训练集中少样本的类别泛化能力会很差。举个例子,我们是一个二分类问题,如果训练集里A类样本占90%,B类样本占10%。而测试集里A类别样本占50%。B类样本占50%,如果不考虑类别不平衡问题,训练出来的模型对于类别B的预测准确率会很低,甚至低于50%。
如何解决这个问题呢?一般方法是:权重法或者采样法
权重法是比较简单的方法,我们可以对训练集里的每个类别加一个权重class weight。如果该类别的样本数多,那么它的权重就低,反之则权重就高。如果更细致点,我们还可以对每个样本加权重sample weight ,思路和类别权重也是一样,即样本数多的类别样本权重低,反之样本权重高。sklearn中,绝大多数算法都有class weight 和sample weight可以使用。
如果权重法做了以后发现预测效果还不好,可以考虑采样法。
采样法也有两种思路,一种是对类别样本数多的样本做子采样,比如训练集里A类别样本占90%,B类样本占10%,那么我们可以对A类的样本子采样,知道子采样得到的A类样本数和B类别现有样本一致为止。这样我们就只用子采样得到的A 类样本数和B类现有样本一起做训练集拟合模型。第二种思路是对类别样本数少的样本做过采样,还是上面的例子,我们对B类别的样本做过采样,知道过采样得到的B类别样本数加上B类别原来样本一起和A类样本数一致,最后再去拟合模型。
上述两种常用的采样法很简单,但是都有个问题,就是采样后改变了训练集的分布,可能导致泛化能力差。所以有的算法就通过其他方法来避免这个问题,比如SMOTE算法通过人工合成的方法来生成少类别的样本。方法也很简单,对于某个缺少样本的类别,它会随机找出几个该类别的样本,再找出最靠近这些样本的若干个该类别样本,组成一个候选合成集合,然后在这个集合中不停的选择距离较近的两个样本,在这两个样本之间,比如中点,构造一个新的该类别样本。举个例子,比如该类别的候选合成集合有两个样本(x1 , y ) , (x2 , y),那么SMOTE采样后,可以得到一个新的训练样本 ((x1+x2)/2 , y),通过这种方法,我们可以得到不改变训练集分布的新样本,让训练集中各个类别的样本数趋于平衡,我们可以用imbalance-learn这个Python库中的SMOTEENN类来做SMOTE采样。
2.9,噪音处理
噪音,是被测量变量的随机误差或方差。我们在上文中提到过异常点(离群点),那么离群点和噪音是不是一回事呢?我们知道,观测量(Measurement) = 真实数据(True Data) + 噪声 (Noise)。离群点(Outlier)属于观测量,既有可能是真实数据产生的,也有可能是噪声带来的,但是总的来说是和大部分观测量之间有明显不同的观测值。。噪音包括错误值或偏离期望的孤立点值,但也不能说噪声点包含离群点,虽然大部分数据挖掘方法都将离群点视为噪声或异常而丢弃。然而,在一些应用(例如:欺诈检测),会针对离群点做离群点分析或异常挖掘。而且有些点在局部是属于离群点,但从全局看是正常的。
那么对于噪音,我们应该如何处理呢?有以下几种方法:
2.9.1,分箱法
- 用箱均值光滑:箱中每一个值被箱中的平均值替换。
- 用箱中位数平滑:箱中的每一个值被箱中的中位数替换。
- 用箱边界平滑:箱中的最大和最小值同样被视为边界。箱中的每一个值被最近的边界值替换。
一般而言,宽度越大,光滑效果越明显。箱也可以是等宽的,其中每个箱值的区间范围是个常量。分箱也可以作为一种离散化技术使用.
2.9.2,回归法
可以用一个函数拟合数据来光滑数据。线性回归涉及找出拟合两个属性(或变量)的“最佳”直线,使得一个属性能够预测另一个。多线性回归是线性回归的扩展,它涉及多于两个属性,并且数据拟合到一个多维面。使用回归,找出适合数据的数学方程式,能够帮助消除噪声。
2.10 去重处理
以DataFrame数据格式为例:
#创建数据,data里包含重复数据
>>> data = pd.DataFrame({'v1':['a']*5+['b']* 4,'v2':[1,2,2,2,3,4,4,5,3]})
>>> data
v1 v2
0 a 1
1 a 2
2 a 2
3 a 2
4 a 3
5 b 4
6 b 4
7 b 5
8 b 3
#DataFrame的duplicated方法返回一个布尔型Series,表示各行是否是重复行
>>> data.duplicated()
0 False
1 False
2 True
3 True
4 False
5 False
6 True
7 False
8 False
dtype: bool
#drop_duplicates方法用于返回一个移除了重复行的DataFrame
>>> data.drop_duplicates()
v1 v2
0 a 1
1 a 2
4 a 3
5 b 4
7 b 5
8 b 3
#这两个方法默认会判断全部列,你也可以指定部分列进行重复项判断。假设你还有一列值,且只希望根据v1列过滤重复项:
>>> data['v3']=range(9)
>>> data
v1 v2 v3
0 a 1 0
1 a 2 1
2 a 2 2
3 a 2 3
4 a 3 4
5 b 4 5
6 b 4 6
7 b 5 7
8 b 3 8
>>> data.drop_duplicates(['v1'])
v1 v2 v3
0 a 1 0
5 b 4 5
#duplicated和drop_duplicates默认保留的是第一个出现的值组合。传入take_last=True则保留最后一个:
>>> data.drop_duplicates(['v1','v2'],take_last = True)
v1 v2 v3
0 a 1 0
3 a 2 3
4 a 3 4
6 b 4 6
7 b 5 7
8 b 3 8
如果数据是列表格式,有以下几种方法可以删除:
list0=['b','c', 'd','b','c','a','a']
方法1:使用set()
list1=sorted(set(list0),key=list0.index) # sorted output
print( list1)
方法2:使用 {}.fromkeys().keys()
list2={}.fromkeys(list0).keys()
print(list2)
方法3:set()+sort()
list3=list(set(list0))
list3.sort(key=list0.index)
print(list3)
方法4:迭代
list4=[]
for i in list0:
if not i in list4:
list4.append(i)
print(list4)
方法5:排序后比较相邻2个元素的数据,重复的删除
def sortlist(list0):
list0.sort()
last=list0[-1]
for i in range(len(list0)-2,-1,-1):
if list0[i]==last:
list0.remove(list0[i])
else:
last=list0[i]
return list0
print(sortlist(list0))
2.11 回顾
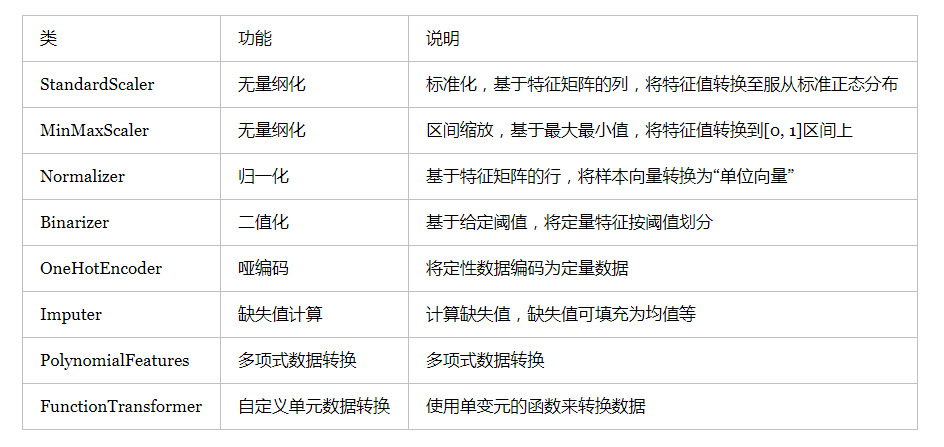
3 特征选择
当数据预处理完成后,我们需要选择有意义的特征输入机器学习的算法和模型进行训练。通常来说,从两个方面考虑来选择特征:
- 特征是否发散(方差筛选):如果一个特征不发散,例如方差接近于0,也就是说样本在这个特征上基本没有差异,这个特征对样本的区分并没有什么用。方差越大,我们可以认为它是比较有用的。在实际应用中,我们会指定一个方差的阈值,当方差小于这个阈值的特征会被我们筛掉,sklearn中的Variable Threshold类可以很方便的完成这个工作。
- 特征与目标的相关性:这点比较明显,与目标相关性高的特征,应当优先选择。除方差法外,我们介绍的其他方法均从相关性考虑。
根据特征选择的形式又可以将特征选择方法分为3种:
- Filter:过滤法:按照发散性或者相关性对各个特征进行评分,设定阈值或者选择阈值的个数,选择特征。
- Wrapper:包装法:根据目标函数(通常是预测效果),每次选择若干特征,护着排除若干特征。
- Embedded:嵌入法:先使用某些机器学习的算法和模型进行训练,得到各个特征的权值系数,根据系数从大到小选择特征。
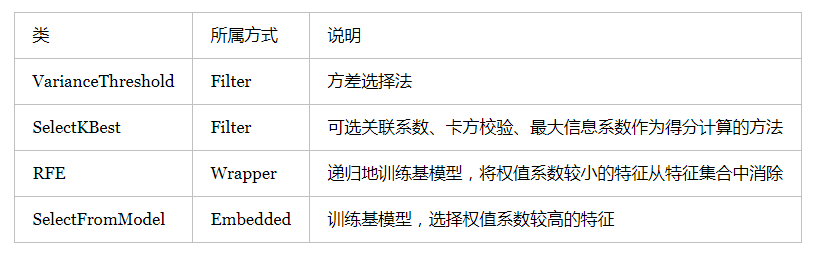
我们使用sklearn中的feature_selection库来进行特征选择。
3.1 Filter
3.1.1 方差选择法
使用方差选择法,先要计算各个特征的方差,然后根据阈值,选择方差大于阈值的特征。使用feature_selection库的VarianceThreshold类来选择特征的代码如下:
from sklearn.feature_selection import VarianceThreshold #方差选择法,返回值为特征选择后的数据 #参数threshold为方差的阈值 VarianceThreshold(threshold=3).fit_transform(iris.data)
3.1.2 相关系数法
使用相关系数法,先要计算各个特征对目标值的相关系数以及相关系数的P值,用feature_selection库的SelectKBest类结合相关系数来选择特征的代码如下:
from sklearn.feature_selection import SelectKBest from scipy.stats import pearsonr #选择K个最好的特征,返回选择特征后的数据 #第一个参数为计算评估特征是否好的函数,该函数输入特征矩阵和目标向量,输出二元组 #(评分,P值)的数组,数组第i项为第i个特征的评分和P值。在此定义为计算相关系数 #参数k为选择的特征个数 SelectKBest(lambda X, Y: array(map(lambda x:pearsonr(x, Y), X.T)).T, k=2).fit_transform(iris.data, iris.target)
3.1.3 卡方检验
经典的卡方检验是检验定性自变量对定性因变量的相关性。假设自变量有N种取值,因变量有M种取值,考虑自变量等于i且因变量等于j的样本频数的观察值与期望的差距,构建统计量:

这个统计量的含义简而言之就是自变量对因变量的相关性,用feature_selection库的SelectKBest类结合卡方检验来选择特征的代码如下:
from sklearn.feature_selection import SelectKBest from sklearn.feature_selection import chi2 #选择K个最好的特征,返回选择特征后的数据 SelectKBest(chi2, k=2).fit_transform(iris.data, iris.target)
3.1.4 互信息法
经典的互信息也是评价定性自变量对定性因变量的相关性的,互信息计算公式如下:
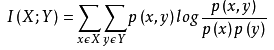
为了处理定量数据,最大信息系数法被提出,使用feature_selection库的SelectKBest类结合最大信息系数法来选择特征的代码如下:
from sklearn.feature_selection import SelectKBest
from minepy import MINE
#由于MINE的设计不是函数式的,定义mic方法将其为函数式的,返回一个二元组,二元组的第2项设置成固定的P值0.5
def mic(x, y):
m = MINE()
m.compute_score(x, y)
return (m.mic(), 0.5)
#选择K个最好的特征,返回特征选择后的数据
SelectKBest(lambda X, Y: array(map(lambda x:mic(x, Y), X.T)).T, k=2).fit_transform(iris.data, iris.target)
3.2 Wrapper
Wrapper方与特征过滤不同,它不单看特征和目标直接的关联性,而是从添加这个特征后模型最终的表现来评估特征的好坏。而在一个特征空间中,产生特征子集的过程可以看成是一个搜索问题。目前主要用的一个Wrapper方法是递归特征消除法。
递归特征消除的主要思想是不断使用从特征空间中抽取出来的特征子集构建模型,然后选出最好的的特征,把选出来的特征放到一遍,然后在剩余的特征上重复这个过程,直到所有特征都遍历了。这个过程中特征被消除的次序就是特征的排序。这是一种寻找最优特征子集的贪心算法。
3.2.1 递归特征消除法
递归特征消除法使用一个基模型来进行多轮训练,每轮训练后,消除若干权值系数的特征,再基于新的特征集进行下一轮训练,使用feature_selection库的RFE类来选择特征的代码如下:
from sklearn.feature_selection import RFE from sklearn.linear_model import LogisticRegression #递归特征消除法,返回特征选择后的数据 #参数estimator为基模型 #参数n_features_to_select为选择的特征个数 RFE(estimator=LogisticRegression(), n_features_to_select=2).fit_transform(iris.data, iris.target)
3.3 Embedded
Embedded方法是在模型构建的同时选择最好的特征。最为常用的一个Embedded方法就是:正则化。正则化就是把额外的约束或者惩罚项加到已有模型的损失函数上,以防止过拟合并提高泛化能力。正则化分为L1正则化(Lasso)和L2正则化(Ridge回归)。
L1正则化是将所有系数的绝对值之和乘以一个系数作为惩罚项加到损失函数上,现在模型寻找最优解的过程中,需要考虑正则项的影响,即如何在正则项的约束下找到最小损失函数。同样的L2正则化也是将一个惩罚项加到损失函数上,不过惩罚项是参数的平方和。其他还有基于树的特征选择等。
3.3.1 基于惩罚项的特征选择法
使用带惩罚项的基模型,除了筛选出特外,同时也进行了降维。使用feature_selection库的SelectFromModel类结合带L1惩罚项的逻辑回归模型,来选择特征的代码如下:
from sklearn.feature_selection import SelectFromModel from sklearn.linear_model import LogisticRegression #带L1惩罚项的逻辑回归作为基模型的特征选择 SelectFromModel(LogisticRegression(penalty="l1", C=0.1)).fit_transform(iris.data, iris.target)
L1惩罚项降维的原理在于保留多个对目标值具有同等相关性的特征中的一个,所以没选到的特征不代表不重要,故可以结合L2惩罚项来优化。具体操作为:若一个特征在L1中的权重为1,选择在L2中的权值差别不大且在L1中权值为0的特征构成同类集合,将这一集合中的特征平分L1中的权值,故需要构建一个新的逻辑回归模型:
from sklearn.linear_model import LogisticRegression
class LR(LogisticRegression):
def __init__(self, threshold=0.01, dual=False, tol=1e-4, C=1.0,
fit_intercept=True, intercept_scaling=1, class_weight=None,
random_state=None, solver='liblinear', max_iter=100,
multi_class='ovr', verbose=0, warm_start=False, n_jobs=1):
#权值相近的阈值
self.threshold = threshold
LogisticRegression.__init__(self, penalty='l1', dual=dual, tol=tol, C=C,
fit_intercept=fit_intercept, intercept_scaling=intercept_scaling, class_weight=class_weight,
random_state=random_state, solver=solver, max_iter=max_iter,
multi_class=multi_class, verbose=verbose, warm_start=warm_start, n_jobs=n_jobs)
#使用同样的参数创建L2逻辑回归
self.l2 = LogisticRegression(penalty='l2', dual=dual, tol=tol, C=C, fit_intercept=fit_intercept, intercept_scaling=intercept_scaling, class_weight = class_weight, random_state=random_state, solver=solver, max_iter=max_iter, multi_class=multi_class, verbose=verbose, warm_start=warm_start, n_jobs=n_jobs)
def fit(self, X, y, sample_weight=None):
#训练L1逻辑回归
super(LR, self).fit(X, y, sample_weight=sample_weight)
self.coef_old_ = self.coef_.copy()
#训练L2逻辑回归
self.l2.fit(X, y, sample_weight=sample_weight)
cntOfRow, cntOfCol = self.coef_.shape
#权值系数矩阵的行数对应目标值的种类数目
for i in range(cntOfRow):
for j in range(cntOfCol):
coef = self.coef_[i][j]
#L1逻辑回归的权值系数不为0
if coef != 0:
idx = [j]
#对应在L2逻辑回归中的权值系数
coef1 = self.l2.coef_[i][j]
for k in range(cntOfCol):
coef2 = self.l2.coef_[i][k]
#在L2逻辑回归中,权值系数之差小于设定的阈值,且在L1中对应的权值为0
if abs(coef1-coef2) < self.threshold and j != k and self.coef_[i][k] == 0:
idx.append(k)
#计算这一类特征的权值系数均值
mean = coef / len(idx)
self.coef_[i][idx] = mean
return self
使用feature_selection库的SelectFromModel类结合带L1以及L2惩罚项的逻辑回归模型,来选择特征的代码如下:
from sklearn.feature_selection import SelectFromModel #带L1和L2惩罚项的逻辑回归作为基模型的特征选择 #参数threshold为权值系数之差的阈值 SelectFromModel(LR(threshold=0.5, C=0.1)).fit_transform(iris.data, iris.target)
3.3.2 基于树模型的特征选择法
树模型中GBDT也可以用来作为基模型来进行特征选择,使用feature_selection库的SelectFromModel类结合GBDT模型,来选择特征的代码如下:
from sklearn.feature_selection import SelectFromModel from sklearn.ensemble import GradientBoostingClassifier #GBDT作为基模型的特征选择 SelectFromModel(GradientBoostingClassifier()).fit_transform(iris.data, iris.target)
3.4 回顾
4 降维
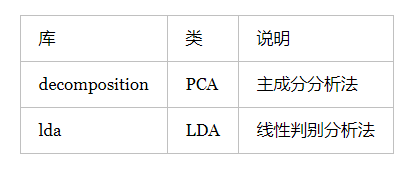
当特征选择完成后,可以直接训练模型了,但是可能由于特征矩阵过大,导致计算量大,训练时间比较长的问题,因此降低特征矩阵维度也是必不可少的。常见的降维方法除了以上提到的基于L1惩罚项的模型以外,另外有主成分分析法(PCA)和线性判别分析(LDA),线性判别分析本身也是一种分类模型。PCA和LDA有很多的相似点,其本质是要将原始的样本映射到维度更低的样本空间中,但是PCA和LDA的映射目标不一样:PCA是为了让映射后的样本具有最大的发散性,而LDA是为了让映射后的样本有最好的分类性能,所以说PCA是一种无监督的降维方法,而LDA是一种有监督的降维方法。
4.1 主成分分析法(PCA)
使用decomposition库的PCA类选择特征的代码如下:
from sklearn.decomposition import PCA #主成分分析法,返回降维后的数据 #参数n_components为主成分数目 PCA(n_components=2).fit_transform(iris.data)
主成分分析原理及其Python实现博文:可以点击这里
4.2 线性判别分析(LDA)
使用lda库的LDA类选择特征的代码如下:
from sklearn.lda import LDA #线性判别分析法,返回降维后的数据 #参数n_components为降维后的维数 LDA(n_components=2).fit_transform(iris.data, iris.target)
线性判别分析原理及其Python实现博文:可以点击这里
4.3 回顾
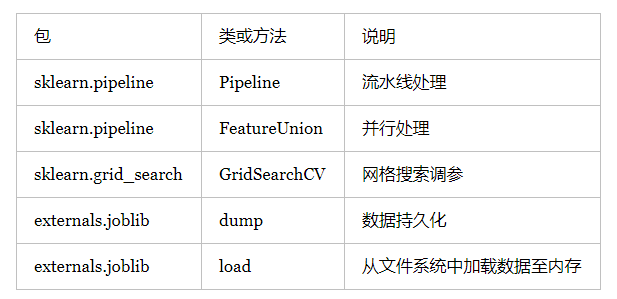
5 使用sklearn进行数据挖掘
那么我们可以使用sklearn完成几乎所有特征处理的工作,而且不管是数据预处理,还是特征选择,抑或降维,他们都是通过某个类的方法fit_transform完成的,fit_transform要不只带一个参数:特征矩阵,要不带两个参数:特征矩阵加目标向量。这些难道都是巧合吗?还是故意设计成这样?方法fit_transform中有fit这一单词,它和训练模型的fit方法有关联吗?
5.1 数据挖掘的步骤
数据挖掘通常包括数据采集,数据分析,特征工程,训练模型,模型评估等步骤。使用sklearn工具可以方便地进行特征工程和模型训练的工作,上面也提到了这些难道都是巧合吗?还是故意设计成这样?方法fit_transform中有fit这一单词,它和训练模型的fit方法有关联吗?
显然,这不是巧合,这是sklearn的设计风格。我们能够更加优雅的使用sklearn进行特征工程和模型训练工作。此时,我们从一个数据挖掘的场景入手:

我们使用sklearn进行虚线框内的工作(sklearn也可以进行文本特征提取),通过分析sklearn源码,我们可以看到除训练,预测和评估以外,处理其他工作的类都实现了3个方法:fit transform fit_transform 。从命名中可以看到,fit_transform方法是先调用fit然后调用transform,我们只需要关注fit方法和transform方法即可。
transform方法主要用来对特征进行转换。从可利用信息的角度来说,转换分为无信息转换和有信息转换。无信息转换是指不利用任何其他信息进行转换,比如指数、对数函数转换等。有信息转换从是否利用目标值向量又可分为无监督转换和有监督转换。无监督转换指只利用特征的统计信息的转换,统计信息包括均值、标准差、边界等等,比如标准化、PCA法降维等。有监督转换指既利用了特征信息又利用了目标值信息的转换,比如通过模型选择特征、LDA法降维等。通过总结常用的转换类,我们得到下表:

不难看出,只有有信息的转换类的fit方法才实际有用,显然fit方法的主要工作是获取特征信息和目标值信息,在这点上,fit方法和模型训练时的fit方法就能够联系在一起了:都是通过分析特征和目标值 ,提取有价值的信息,对于转换类来说是某些统计量,对于模型来说可能是特征的权值系数等。另外,只有有监督的转换类的fit和transform方法才需要特征和目标值两个参数。fit方法无用不代表没实现,而是除合法性校验以外,其并没有对特征和目标值进行任何处理,Normalizer的fit方法实现如下:
def fit(self, X, y=None):
"""Do nothing and return the estimator unchanged
This method is just there to implement the usual API and hence
work in pipelines.
"""
X = check_array(X, accept_sparse='csr')
return self
基于这些特征处理工作都有共同的方法,那么试想可不可以将他们组合在一起?在本文假设的场景中,我们可以看到这些工作的组合形式有两种:流水线式和并行式。基于流水线组合的工作需要依次进行,前一个工作的输出是后一个工作的输入;基于并行式的工作可以同时进行,其使用同样的输入,所有工作完成后将各自的输出合并之后输出。sklearn提供了包pipeline来完成流水线式和并行式的工作。
5.1.1 数据初貌
在此,我们仍然使用IRIS数据集来进行说明,为了适应提出的场景,对元数据集需要稍微加工:
from numpy import hstack, vstack, array, median, nan from numpy.random import choice from sklearn.datasets import load_iris #特征矩阵加工 #使用vstack增加一行含缺失值的样本(nan, nan, nan, nan) #使用hstack增加一列表示花的颜色(0-白、1-黄、2-红),花的颜色是随机的,意味着颜色并不影响花的分类 iris.data = hstack((choice([0, 1, 2], size=iris.data.shape[0]+1).reshape(-1,1), vstack((iris.data, array([nan, nan, nan, nan]).reshape(1,-1))))) #目标值向量加工 #增加一个目标值,对应含缺失值的样本,值为众数 iris.target = hstack((iris.target, array([median(iris.target)])))
5.1.2 关键技术
并行处理,流水线处理,自动化调参,持久化是使用sklearn优雅的进行数据挖掘的核心。并行处理和流水线处理将多个特征处理工作,甚至包括模型训练工作组合成一个工作(从代码的角度来说,即将多个对象组成了一个对象)。在组合的前提下,自动化调参技术帮我们省去了人工调参的繁琐。训练好的模型是储存在内存中的数据,持久化能够将这些数据保存在文件系统中,之后使用时候无需再进行训练,直接从文件系统中加载即可。
5.2 并行处理
并行处理使得多个特征处理工作能够并行的进行,根据对特征矩阵的读取方式不同,可分为整体并行处理和部分并行处理。整体并行处理,即并行处理的每个工作的输入都是特征矩阵的整体;部分并行处理,即可定义每个工作需要输入的特征矩阵的列。
5.2.1 整体并行处理
pipeline包提供了FeatureUnion类来进行整体并行处理:
from numpy import log1p
from sklearn.preprocessing import FunctionTransformer
from sklearn.preprocessing import Binarizer
from sklearn.pipeline import FeatureUnion
#新建将整体特征矩阵进行对数函数转换的对象
step2_1 = ('ToLog', FunctionTransformer(log1p))
#新建将整体特征矩阵进行二值化类的对象
step2_2 = ('ToBinary', Binarizer())
#新建整体并行处理对象
#该对象也有fit和transform方法,fit和transform方法均是并行地调用需要并行处理的对象的fit和transform方法
#参数transformer_list为需要并行处理的对象列表,该列表为二元组列表,第一元为对象的名称,第二元为对象
step2 = ('FeatureUnion', FeatureUnion(transformer_list=[step2_1, step2_2, step2_3]))
5.2.2 部分并行处理
整体并行处理有其缺陷,在一些场景下,我们只需要对特征矩阵的某些列进行转换,而不是所有列,pipeline并没有提供相应的类(仅OneHotEncoder类实现了该功能)需要我们再FeatureUnion的基础上进行优化:
from sklearn.pipeline import FeatureUnion, _fit_one_transformer, _fit_transform_one, _transform_one
from sklearn.externals.joblib import Parallel, delayed
from scipy import sparse
import numpy as np
#部分并行处理,继承FeatureUnion
class FeatureUnionExt(FeatureUnion):
#相比FeatureUnion,多了idx_list参数,其表示每个并行工作需要读取的特征矩阵的列
def __init__(self, transformer_list, idx_list, n_jobs=1, transformer_weights=None):
self.idx_list = idx_list
FeatureUnion.__init__(self, transformer_list=map(lambda trans:(trans[0], trans[1]), transformer_list), n_jobs=n_jobs, transformer_weights=transformer_weights)
#由于只部分读取特征矩阵,方法fit需要重构
def fit(self, X, y=None):
transformer_idx_list = map(lambda trans, idx:(trans[0], trans[1], idx), self.transformer_list, self.idx_list)
transformers = Parallel(n_jobs=self.n_jobs)(
#从特征矩阵中提取部分输入fit方法
delayed(_fit_one_transformer)(trans, X[:,idx], y)
for name, trans, idx in transformer_idx_list)
self._update_transformer_list(transformers)
return self
#由于只部分读取特征矩阵,方法fit_transform需要重构
def fit_transform(self, X, y=None, **fit_params):
transformer_idx_list = map(lambda trans, idx:(trans[0], trans[1], idx), self.transformer_list, self.idx_list)
result = Parallel(n_jobs=self.n_jobs)(
#从特征矩阵中提取部分输入fit_transform方法
delayed(_fit_transform_one)(trans, name, X[:,idx], y,
self.transformer_weights, **fit_params)
for name, trans, idx in transformer_idx_list)
Xs, transformers = zip(*result)
self._update_transformer_list(transformers)
if any(sparse.issparse(f) for f in Xs):
Xs = sparse.hstack(Xs).tocsr()
else:
Xs = np.hstack(Xs)
return Xs
#由于只部分读取特征矩阵,方法transform需要重构
def transform(self, X):
transformer_idx_list = map(lambda trans, idx:(trans[0], trans[1], idx), self.transformer_list, self.idx_list)
Xs = Parallel(n_jobs=self.n_jobs)(
#从特征矩阵中提取部分输入transform方法
delayed(_transform_one)(trans, name, X[:,idx], self.transformer_weights)
for name, trans, idx in transformer_idx_list)
if any(sparse.issparse(f) for f in Xs):
Xs = sparse.hstack(Xs).tocsr()
else:
Xs = np.hstack(Xs)
return Xs
在本文提出的场景中,我们对特征矩阵的第1列(花的颜色)进行定性特征编码,对第2,3,4列进行对数函数转换,对第5列进行定量特征二值化处理。使用FeatureUnionExt类进行部分并行处理的代码如下:
from numpy import log1p
from sklearn.preprocessing import OneHotEncoder
from sklearn.preprocessing import FunctionTransformer
from sklearn.preprocessing import Binarizer
#新建将部分特征矩阵进行定性特征编码的对象
step2_1 = ('OneHotEncoder', OneHotEncoder(sparse=False))
#新建将部分特征矩阵进行对数函数转换的对象
step2_2 = ('ToLog', FunctionTransformer(log1p))
#新建将部分特征矩阵进行二值化类的对象
step2_3 = ('ToBinary', Binarizer())
#新建部分并行处理对象
#参数transformer_list为需要并行处理的对象列表,该列表为二元组列表,第一元为对象的名称,第二元为对象
#参数idx_list为相应的需要读取的特征矩阵的列
step2 = ('FeatureUnionExt', FeatureUnionExt(transformer_list=[step2_1, step2_2, step2_3], idx_list=[[0], [1, 2, 3], [4]]))
5.3 流水线处理
pipeline包提供了Pipeline类来进行流水线处理,流水线上除最后一个工作以外,其他都要执行fit_transfrom方法,且上一个工作输出作为下一个工作的输入。最后一个工作必须实现fit方法,输入为上一个工作的输出;但是不限定一定有transform方法,因为流水线的最后一个工作可能是训练!
根据文中提出的场景,结合并行处理,构造完整的流水线的代码如下:
from numpy import log1p
from sklearn.preprocessing import Imputer
from sklearn.preprocessing import OneHotEncoder
from sklearn.preprocessing import FunctionTransformer
from sklearn.preprocessing import Binarizer
from sklearn.preprocessing import MinMaxScaler
from sklearn.feature_selection import SelectKBest
from sklearn.feature_selection import chi2
from sklearn.decomposition import PCA
from sklearn.linear_model import LogisticRegression
from sklearn.pipeline import Pipeline
#新建计算缺失值的对象
step1 = ('Imputer', Imputer())
#新建将部分特征矩阵进行定性特征编码的对象
step2_1 = ('OneHotEncoder', OneHotEncoder(sparse=False))
#新建将部分特征矩阵进行对数函数转换的对象
step2_2 = ('ToLog', FunctionTransformer(log1p))
#新建将部分特征矩阵进行二值化类的对象
step2_3 = ('ToBinary', Binarizer())
#新建部分并行处理对象,返回值为每个并行工作的输出的合并
step2 = ('FeatureUnionExt', FeatureUnionExt(transformer_list=[step2_1, step2_2, step2_3], idx_list=[[0], [1, 2, 3], [4]]))
#新建无量纲化对象
step3 = ('MinMaxScaler', MinMaxScaler())
#新建卡方校验选择特征的对象
step4 = ('SelectKBest', SelectKBest(chi2, k=3))
#新建PCA降维的对象
step5 = ('PCA', PCA(n_components=2))
#新建逻辑回归的对象,其为待训练的模型作为流水线的最后一步
step6 = ('LogisticRegression', LogisticRegression(penalty='l2'))
#新建流水线处理对象
#参数steps为需要流水线处理的对象列表,该列表为二元组列表,第一元为对象的名称,第二元为对象
pipeline = Pipeline(steps=[step1, step2, step3, step4, step5, step6])
5.4 自动化调参
网格搜索为自动化调参的常用技术之一,grid_search包提供了自动化调参的工具,包括GridSearchCV类。对组合好的对象进行训练以及调参的代码如下:
from sklearn.grid_search import GridSearchCV
#新建网格搜索对象
#第一参数为待训练的模型
#param_grid为待调参数组成的网格,字典格式,键为参数名称(格式“对象名称__子对象名称__参数名称”),值为可取的参数值列表
grid_search = GridSearchCV(pipeline, param_grid={'FeatureUnionExt__ToBinary__threshold':[1.0, 2.0, 3.0, 4.0], 'LogisticRegression__C':[0.1, 0.2, 0.4, 0.8]})
#训练以及调参
grid_search.fit(iris.data, iris.target)
5.5 持久化
externals.joblib包提供了dump和load方法来持久化和加载内存数据:
#持久化数据
#第一个参数为内存中的对象
#第二个参数为保存在文件系统中的名称
#第三个参数为压缩级别,0为不压缩,3为合适的压缩级别
dump(grid_search, 'grid_search.dmp', compress=3)
#从文件系统中加载数据到内存中
grid_search = load('grid_search.dmp')
5.6 回顾
注意:组合和持久化都会涉及pickle技术,在Sklearn的技术文档中有说明,将lambda定义函数作为FunctionTransformer的自定义转换函数将不能pickle化。
知识扩展:Python忽略warning警告错误
Python开发中经常遇到报错的情况,但是warning通常不影响程序的运行,而且有时候特别讨厌,下面我们来说下如何忽略warning的错误。
在说忽略warning之前,我们先说下如何主动产生warning错误,这里用到warnings模块,看如下代码:
import warnings
def fxn():
warnings.warn("deprecated", DeprecationWarning)
with warnings.catch_warnings():
warnings.simplefilter("ignore")
fxn()
这样就产生了warning错误
那么如何来控制警告错误的输出呢?很简单
import warnings
warnings.filterwarnings('ignore')
这样就忽略了警告错误的输出。
如何忽略命令行下警告输出呢?
python -W ignore yourscript.py
参考资料:http://www.cnblogs.com/jasonfreak/p/5448462.html
http://www.cnblogs.com/jasonfreak/p/5448385.html
https://www.cnblogs.com/pinard/p/9093890.html
(在此做笔记的目的是学习,并掌握特征工程,不喜勿喷,谢谢)