概率密度函数、概率分布函数、概率质量函数

1.概率密度函数

　　1.1. 定义

　　　　如果对于随机变量X的分布函数F(x),存在非负函数f(x),使得对于任意实数有

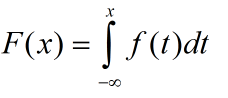
　　　　则称X为连续型随机变量，其中F(x)称为X的概率密度函数，简称概率密度。（f(x)>=0,若f(x)在点x处连续则F(x)求导可得）f(x)并没有很特殊的意义，但是通过其值得相对大小得知，若f(x)越大，对于同样长度的区间，X落在这个区间的概率越大。

 

　　1.2.意义及通俗解释

 

   　　A.形象解释：

 

　　　　这么说吧，一个物体，问你它在某一个点处的质量是多少 ？ 因为一个点是无限小的，所以点的质量一定为0。然而这个物体是由无数个点组成的，假如我们又需要求它质量，怎么办呢 ？于是引入密度的概念 ,最后再把密度积分就可以得到质量m了。

　　　　同理，如果在[0，1]上随机取点，求取在某一点处的概率，点的长度无限小，此概率一定为0。这时情况和上面所述类似，我们需要引入概率密度p，其中p= 。这样我们就可以求所取点落在某一段(a,b)上的概率了。概率p= 。

 

　　　　总结:为什么要叫概率密度，因为它和物理上密度的定义本质上是一样的。我们做题的时候一般就两种。一.告诉你概率密度函数，让你求分布函数，积分就好了。二.告诉你分布函数，让你求概率密度函数，求导就好了。

就像你做初中物理的密度题，无非两种:一.告诉你物体的密度让你求质量。二.告诉你物体的质量让你求密度。

   　　B.实例说明

 

　　　　概率密度函数可以看成是直方图的平滑近似。

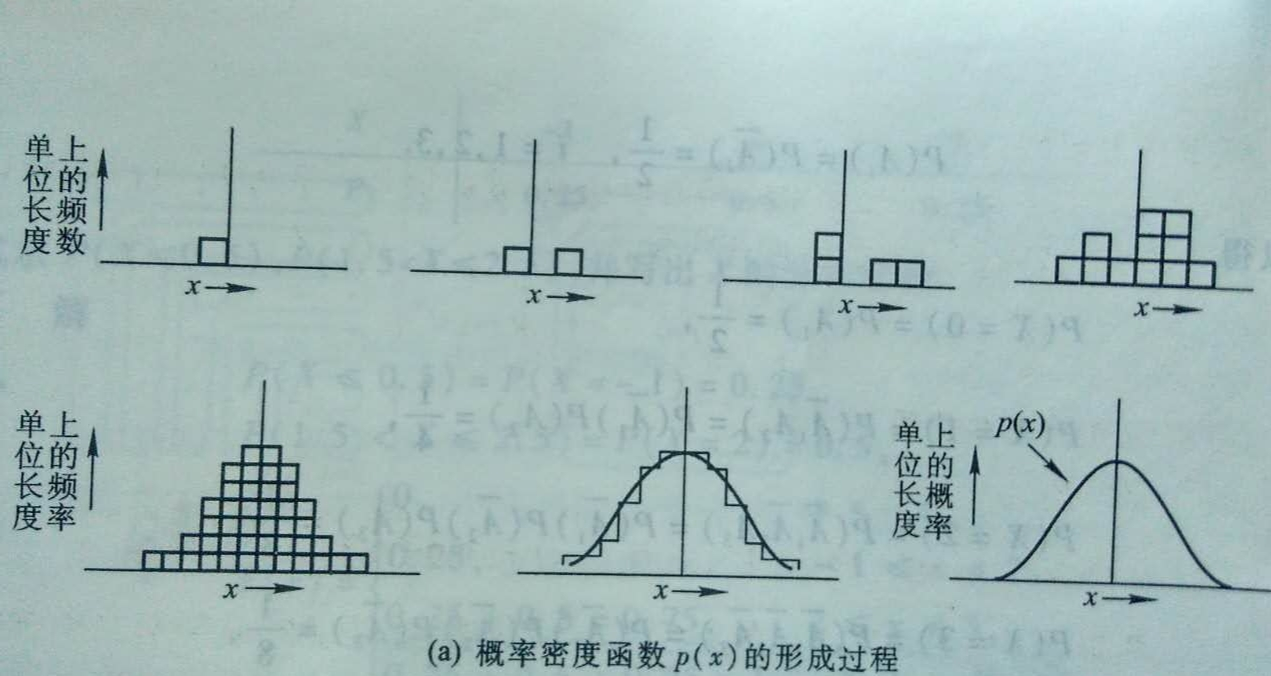　　1.3.概率密度函数和概率的关系

 

　　　　这里有一点绕人，只有连续型函数才有概率密度！

　　　　某一点的值是没有概率的P(X=1) = 0; 

　　　　某一段的概率：设F(x)是概率分布函数，如果f(x)在[-无穷,x]的积分就是F(x)，f(x)>=0,则乘f(x)为x的概率密度函数。

　　　　概率分布求导数就是概率分布函数！

 

　　1.4.函数间的概率密度关系

 

　　　　注释：这里完全是我个人理解，没找到相关资料，只是看到有人这么用，有可能是错误的，欢迎指正！

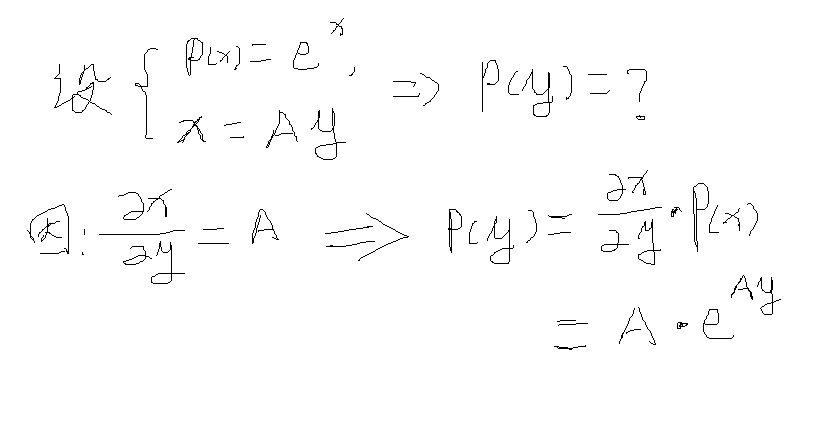2.概率分布函数　　

　　

　　P=P(t<=X)

 

3.概率分布函数

 

　  离散函数的概率值:P=P(K=X)

 

4.相互关系以及求解实例

 

　　4.1给定概率密度

　　　　

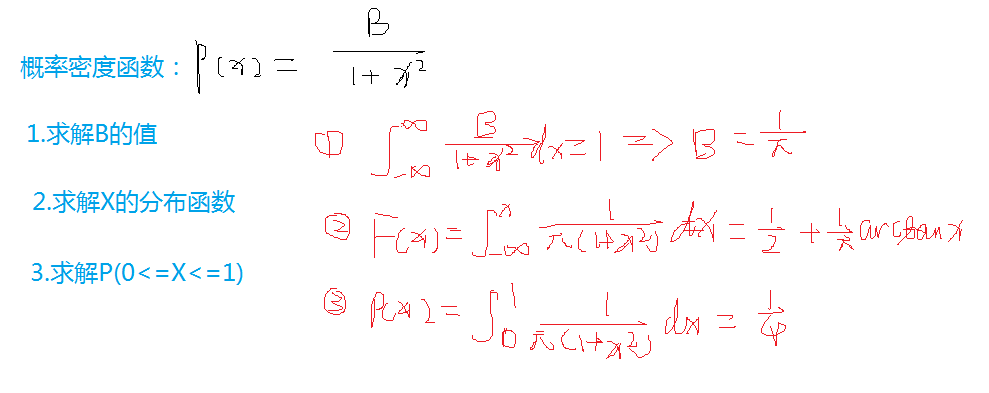
　　4.2给定分布函数

　　4.3给定正常函数

　　　　注释：这里是我自己想的，没有看到别的地方写，如有错误欢迎指正！

参考：http://www.cnblogs.com/jstong/p/5903641.html

　　　https://www.zhihu.com/question/23237834

 　　　   https://www.cnblogs.com/dengdan890730/p/6169159.html