1.朴素贝叶斯的多项式事件模型:
趁热打铁,直接看图理解模型的意思:具体求解可见下面大神给的例子,我这个是流程图。
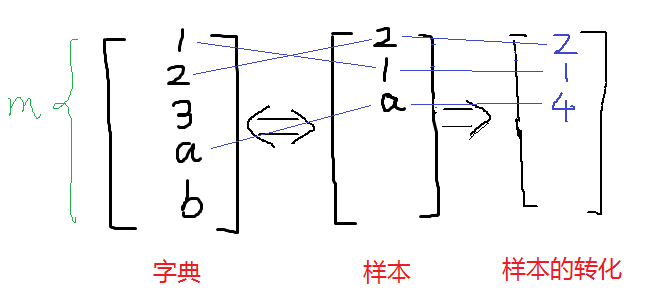

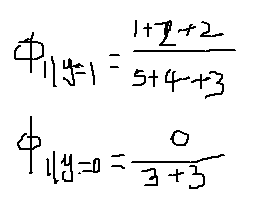
在上篇笔记中,那个最基本的NB模型被称为多元伯努利事件模型(Multivariate Bernoulli Event Model,以下简称 NB-MBEM)。该模型有多种扩展,一种是在上一篇笔记中已经提到的每个分量的多值化,即将p(xi|y)由伯努利分布扩展到多项式分布;还有一种在上一篇笔记中也已经提到,即将连续变量值离散化。本文将要介绍一种与多元伯努利事件模型有较大区别的NB模型,即多项式事件模型(Multinomial Event Model,一下简称NB-MBEM)。
首先 ,NB-MEM改变了特征向量的表示方法。在 NB-MBEM中,特征向量的每个分量代表词典中该index上的词语是否在文本中出现过,其取值范围为{0,1},特征向量的长度为词典的大小。而在 NB-MEM中,特征向量中的每个分量的值是文本中处于该分量的位置的词语在词典中的索引,其取值范围是{1,2,...,|V|},|V|是词典的大小,特征向量的长度为相应样例文本中词语的数目。
形式化表示为:
m个训练样本表示为:{x(i),y(i);i=1,...,m}
x(i)=(x1(i),x2(i),...,xni(i))
表示第i个样本中,共有ni个词,每个词在字典的编号xj(i)。
举例来说,在NB-MBEM中,一篇文档的特征向量可能如下所示:
其在NB-MEM中的向量表示则如下所示
在NB-MEM中,假设文本的生成过程如下:
1、确定文本的类别,比如是否为垃圾文本、是财经类还是教育类;
2、遍历文本的各个位置,以相同的多项式分布生成各个词语,生成词语时相互独立。
由上面的生成过程可知,NB-MEM假设文本类别服从多项式分布或伯努利分布,而词典中所有的词语服从多项式分布。生成过程还可如下解释,即现在类别所服从的多项式分布中选取类别,然后遍历整个文本,在词语所服从的多项式分布中选取词语,放在文本中相应的位置上。
于是,NB-MEM的参数如下所示:
于是,我们可以得到参数在训练集上的极大似然估计:
在φk|y=1和φk|y=0 上使用Laplace平滑,得到公式如下:
其中,|V|为词典的大小。
与以前的式子相比,分母多了个ni,分子由0/1变成了k。
对于式子
分子的意思是对所有标签为1的邮件求和,即只考虑垃圾邮件,之后对垃圾邮件中的所有词求和,它加起来应该是词k出现在垃圾邮件中的次数。
换句话说,分子实际上就是对训练集合中的所有垃圾邮件中词k出现的次数进行求和。
分母的含义是对训练样本集合进行求和,如果其中的一个样本是垃圾邮件(y=1),那么就把它的长度加起来,所以分母的含义是训练集合中所有垃圾邮件的总长。
所以这个比值的含义就是在所有垃圾邮件中,词k所占的比例。
假如邮件中只有a,b,c这三个词,他们在词典的位置分别是1,2,3,前两封邮件都只有两个词,后两封有3个词。
Y=1是垃圾邮件。
那么,
假如新来一封邮件为b,c,那么特征表示为{2,3}
那么
那么该邮件是垃圾邮件概率是0.6。
注意这个公式与朴素贝叶斯的不同在于这里针对整体样本求的φk|y=1 ,而朴素贝叶斯里面针对每个特征求的φxj=1|y=1 ,而且这里的特征值维度是参差不齐的。
2.神经网络
这就不说了,很早之前就已经推到过而且写过代码-->>http://www.cnblogs.com/wjy-lulu/p/6547542.html
3.支持向量机
以前看过懂了,时间长不用又忘记了,这个等用到再看吧
http://www.cnblogs.com/wjy-lulu/p/6979436.html
参考:http://blog.sina.com.cn/s/blog_8a951ceb0102wbbv.html(这里面说的例子很好,我感觉画示意图就行了,再写例子太浪费时间了)