第六部分内容:
1.偏差/方差(Bias/variance)
2.经验风险最小化(Empirical Risk Minization,ERM)
3.联合界(Union bound)
4.一致收敛(Uniform Convergence)
第七部分内容:
1. VC 维
2.模型选择(Model Selection)
2017.11.3注释:这两个部分都是讲述理论过程的,第一方面太难了,第二方面现在只想快速理解Ng的20节课程。所以这部分以后回头再看!
2017.11.4注释:这理论还是得掌握,不然看Ng视频干嘛?直接去操作TF算了啊。。。。
1.偏差/方差(Bias/variance)
https://www.gitbook.com/book/yoyoyohamapi/mit-ml/details,这个是比较简单的,偷懒不写了。
2.经验风险最小化(Empirical Risk Minization,ERM)
定义一个线性分类器
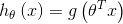
其中  (note
(note  )
)
假设有m个训练样本,样本之间是独立同分布的。
定义训练误差:
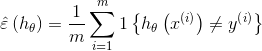
训练误差也被称为风险。
经验风险最小化: 选择分类器函数的参数,使得分类器的训练误差(training error)最小。

让我们换一种考虑方式:我们不是在选择最优分类器函数的参数,而是在选择最优的分类器函数。
定义假设类

假设类的每一个成员都是参数n+1个的线性分类器函数。
重新定义ERM:从假设类H中选取一个函数,使得分类器的训练误差最小。

实际上,我们并不关心训练误差的大小,我们关心的是分类器对于未知样本的预测能力,也就是一般误差(generation error):

3.联合界(Union bound)
注释:这里的两个定理证明很麻烦,直接用就可以了,联合界定理很简单不用叙述,Hoeffding 不等式表示试验次数越多均值越趋向真实的值,比如实验10000次硬币,那就正反的比例为1:1。
3.1.联合界引理(Union Bound):
令  表示k个事件,这些事件不一定是独立的,
表示k个事件,这些事件不一定是独立的,
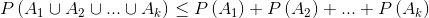
3.2.Hoeffding 不等式:
假设Z1,…,Zm为m个独立同分布(iid,independent and identically distributed)的随机变量,服从于伯努利分布,即


并且
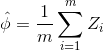
为这些随机变量的均值,给定  ,那么有
,那么有

表达的是对真实分布的估计值与真实分布之间的差值大于 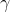 的概率的上界,这个上界随着m的增加而指数下降。
的概率的上界,这个上界随着m的增加而指数下降。
考虑具有有限假设类的情形: 猜想类H具有k个假设
猜想类H具有k个假设
ERM会从H中选出具有最小训练误差的假设

注释:对Hoeffding 不等式的简单解释如下-->>
Hoeffding不等式是关于一组随机变量均值的概率不等式。 如果X1,X2,⋯,Xn为一组独立同分布的参数为p的伯努利分布随机变量,n为随机变量的个数。定义这组随机变量的均值为:

对于任意δ>0, Hoeffding不等式可以表示为
![]()
上面的公式似乎写的不是很详细,所以我又从网上copy了一份其他的解释:
Hoeffding不等式:Hoeffding不等式好像有很多个形式,all of statistics里的感觉较难理解,这里写一种好理解的。令X1,…,Xn为独立同分布随机变量,满足ai≤Xi≤bi。则对于任意t>0有

其中:
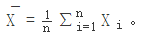
至于这个公式怎么证明,就不要为难自己了~
而这个公式的用途:
在统计推断中,我们可以利用样本的统计量(statistic)来推断总体的参数(parameter),譬如使用样本均值来估计总体期望。如下图所示,我们从罐子里抽球,希望估计罐子里红球和绿球的比例。

直觉上,如果我们有更多的样本(抽出更多的球),则样本期望ν应该越来越接近总体期望μ。事实上,这里可以用hoeffding不等式表示如下:

从hoeffding不等式可以看出,当n逐渐变大时,不等式的UpperBound越来越接近0,所以样本期望越来越接近总体期望。
4.一致收敛(Uniform Convergence)
4.1. 训练误差是一个对一般误差的很好的近似
首先证明第一项,从猜想类H中任意选取一个假设  ,定义
,定义
 服从伯努利分布,因此
服从伯努利分布,因此
 其均值是假设的一般误差。
其均值是假设的一般误差。
训练误差为

由Hoeffding不等式可知

假设m很大,即训练样本很多,那么训练误差将会以很大概率近似于一般误差。
定义事件  为
为  发生
发生
有

那么对于整个猜想类来说

= 

两边同时用1减去



也就是说,在不小于  的概率下,对于猜想类H中的所有假设h,其训练误差和一般误差之间的差距将会在
的概率下,对于猜想类H中的所有假设h,其训练误差和一般误差之间的差距将会在 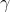 以内。
以内。
这被称为 一致收敛。
4.2. ERM选择的假设的一般误差存在上界
定义
那么给定  和
和 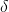 解出
解出


意思是,只要你的训练集合包含至少上述m这么多的样本,那么概率至少在  下,有
下,有  对H中的所有假设成立。
对H中的所有假设成立。
样本复杂度:为了达到一个特定的错误的界,你需要多大的训练集合。
误差界:
同样的,我们可以固定m和
定义 为H中具有最小一般误差的假设,
为H中具有最小一般误差的假设, 为H中具有最小训练误差的假设,那么至少在
为H中具有最小训练误差的假设,那么至少在  的概率下,有
的概率下,有






也就是说,我们选择的(具有最小训练误差的)假设的一般误差,和具有最小一般误差的假设的一般误差之间的差值存在  的上界。
的上界。
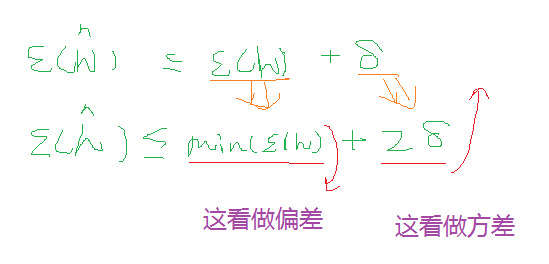
直观上,我们可以把第一项  看成是选择假设的偏差,第二项
看成是选择假设的偏差,第二项  看成选择假设的方差。
看成选择假设的方差。
当我们将H替换为更复杂的猜想类H',即H是H'的子集时,第一项只会变的更小,即偏差变小;而由于k的增大,第二项会变的更大,即方差变大。
将一切总结为两个定理如下:


第七部分:
7.1VC维空间,VC界讲的很棒
7.2模型选择
7.1.1.交叉验证
训练和测试相互参照
7.1.2特征选择
控制变量,去观察别的变量对结果的影响
7.1.3特征过滤
计算特征Xi和Y的相关程度,然后再通过交叉验证去排除
