LeetCode解题记录(贪心算法)（一）

1. 前言

目前得到一本不错的算法书籍，页数不多，挺符合我的需要，于是正好借这个机会来好好的系统的刷一下算法题，一来呢，是可以给部分同学提供解题思路，和一些自己的思考，二来呢，我也可以在需要复习的时候，通过博客来回顾自己,废话不多说，开始！
目前的规划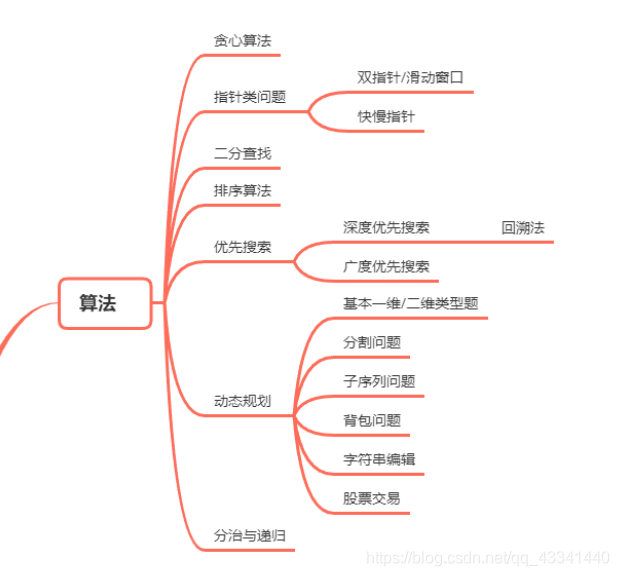

2. 算法解释

顾名思义，贪心算法或贪心思想采用贪心的策略，保证每次操作都是局部最优的，从而使最后得到的结果是全局最优的。

举一个最简单的例子：小明和小王喜欢吃苹果，小明可以吃五个，小王可以吃三个。已知苹果园里有吃不完的苹果，求小明和小王一共最多吃多少个苹果。在这个例子中，我们可以选用的贪心策略为，每个人吃自己能吃的最多数量的苹果，这在每个人身上都是局部最优的。又因为全局结果是局部结果的简单求和，且局部结果互不相干，因此局部最优的策略也同样是全局最优的策略。

如果还是不明白的同学可以自己去百度哈，我相信贪心算法是不难懂的

455 Assign Cookies (Easy)

题目地址

这题的思路就是，优先满足胃口小的孩子，而且是优先选择尺寸接近孩子的饼干给他，那么这就是一个贪心的思想，即希望每个孩子给的饼干尽可能的接近他的胃口
算法思路就是，先将两个数组排序，然后遍历，如果发现饼干大于等于孩子的胃口值，则给这个孩子，两边的索引同时+1，同时count+1，如果小于，则饼干的vector的索引+1

下面是我的代码，可能不够优雅，大家觉得哪些地方需要改进，可以在下面提出来

class Solution {
public:
    int findContentChildren(vector<int>& g, vector<int>& s) {
        sort(g.begin(),g.end());
        sort(s.begin(),s.end());
        int gsize = g.size();
        int ssize = s.size();
        int i=0,j=0;
        int count=0;
        while(i<gsize && j<ssize ){
            // 能被满足
            if(s[j]>=g[i]){
                i++;
                j++;
                count++;
            }else{
                j++;
            }
        }

        return count;
    }
};

122. 买卖股票的最佳时机 II

题目地址
给定一个数组 prices ，其中 prices[i] 是一支给定股票第 i 天的价格。

设计一个算法来计算你所能获取的最大利润。你可以尽可能地完成更多的交易（多次买卖一支股票）。

注意：你不能同时参与多笔交易（你必须在再次购买前出售掉之前的股票）。

示例 1:

输入: prices = [7,1,5,3,6,4]
输出: 7
解释: 在第 2 天（股票价格 = 1）的时候买入，在第 3 天（股票价格 = 5）的时候卖出, 这笔交易所能获得利润 = 5-1 = 4 。
随后，在第 4 天（股票价格 = 3）的时候买入，在第 5 天（股票价格 = 6）的时候卖出, 这笔交易所能获得利润 = 6-3 = 3 。

示例 2:

输入: prices = [1,2,3,4,5]
输出: 4
解释: 在第 1 天（股票价格 = 1）的时候买入，在第 5 天 （股票价格 = 5）的时候卖出, 这笔交易所能获得利润 = 5-1 = 4 。
注意你不能在第 1 天和第 2 天接连购买股票，之后再将它们卖出。因为这样属于同时参与了多笔交易，你必须在再次购买前出售掉之前的股票。

示例 3:

输入: prices = [7,6,4,3,1]
输出: 0
解释: 在这种情况下, 没有交易完成, 所以最大利润为 0。

提示：

1 <= prices.length <= 3 * 104
0 <= prices[i] <= 104

这题的思路还是贪心算法，虽然动态规划算法也可以写，但是这是贪心专题，就不扩展了

贪心就是指根据目前的情况来判断，获得每一步的最大值，而不需要考虑其他，在这题里面就是考虑我怎么获得钱的最大值，很明显，只要第二天的股票比今天贵，我就卖掉，这样就一定能赚钱，有人可能会想，我第一天买，第二天卖，但是第二天不能买啊，按照题目意思，确实是这样的，但是可以自己推导一下

比如，[1,2,3,4],这是4天的股票价格，那么按照贪心算法是，（2-1）+（3-2）+（4-3） = 4-1
所以等价于我们第一天买，最后一天卖

代码如下

class Solution {
public:
    int maxProfit(vector<int>& prices) {
        
        int res = 0;
        if(prices.size() == 1){
            return 0;
        }
        for (int i = 1; i < prices.size(); i++) {
            int diff = prices[i] - prices[i - 1];
            if (diff > 0) {
                res += diff;
            }
        }
        return res;
    }
};

力扣提交结果

135. 分发糖果

题目链接

老师想给孩子们分发糖果，有 N 个孩子站成了一条直线，老师会根据每个孩子的表现，预先给他们评分。

你需要按照以下要求，帮助老师给这些孩子分发糖果：

每个孩子至少分配到 1 个糖果。
评分更高的孩子必须比他两侧的邻位孩子获得更多的糖果。
那么这样下来，老师至少需要准备多少颗糖果呢？

示例 1：

输入：[1,0,2]
输出：5
解释：你可以分别给这三个孩子分发 2、1、2 颗糖果。
示例 2：

输入：[1,2,2]
输出：4
解释：你可以分别给这三个孩子分发 1、2、1 颗糖果。
第三个孩子只得到 1 颗糖果，这已满足上述两个条件。

把所有孩子的糖果数初始化为 1；
先从左往右遍历一遍，如果右边孩子的评分比左边的高，则右边孩子的糖果数更新为左边孩子的
糖果数加 1；再从右往左遍历一遍，如果左边孩子的评分比右边的高，且左边孩子当前的糖果数
不大于右边孩子的糖果数，则左边孩子的糖果数更新为右边孩子的糖果数加 1。通过这两次遍历，
分配的糖果就可以满足题目要求了。这里的贪心策略即为，在每次遍历中，只考虑并更新相邻一
侧的大小关系。

不理解的，可以在纸上自己画一画，就容易理解啦

代码如下

#include <iostream>
#include <vector>
#include <numeric>
using namespace std;

int candy(vector<int>& ratings) {
	int len = ratings.size();
	if (len < 2) {
		return len;
	}
	vector<int>  cd(len, 1);

	for (int i = 1; i < len; i++) {
		if (ratings[i] > ratings[i - 1]) {
			cd[i] = cd[i - 1] + 1;
		}
	}

	for (int i = len - 2; i >= 0; i--) {
		if (ratings[i] > ratings[i + 1]) {
			if (cd[i] <= cd[i + 1]) {
				cd[i] = cd[i + 1] + 1;
			}
		}
	}

	//for (auto a : cd) {
	//	cout << a << " ";
	//}

	// 0这个参数代表整数求和，0. 代表浮点数求和
	return accumulate(cd.begin(), cd.end(), 0);
}
int main() {
	vector<int> a = { 1,3,4,5,2 };
	cout << candy(a);
	return 0;
}

435. 无重叠区间

题目链接

给定一个区间的集合，找到需要移除区间的最小数量，使剩余区间互不重叠。

注意:

可以认为区间的终点总是大于它的起点。
区间 [1,2] 和 [2,3] 的边界相互“接触”，但没有相互重叠。
示例 1:

输入: [ [1,2], [2,3], [3,4], [1,3] ]

输出: 1

解释: 移除 [1,3] 后，剩下的区间没有重叠。
示例 2:

输入: [ [1,2], [1,2], [1,2] ]

输出: 2

解释: 你需要移除两个 [1,2] 来使剩下的区间没有重叠。
示例 3:

输入: [ [1,2], [2,3] ]

输出: 0

解释: 你不需要移除任何区间，因为它们已经是无重叠的了。

在选择要保留区间时，区间的结尾十分重要：选择的区间结尾越小，余留给其它区间的空间
就越大
（这里用到了贪心的思想，我们希望每一个区间的结尾最小且不会重叠，这样得到的区间就一定是最大的）
就越能保留更多的区间。因此，我们采取的贪心策略为，优先保留结尾小且不相交的区
间。
具体实现方法为，先把区间按照结尾的大小进行增序排序，每次选择结尾最小且和前一个选
择的区间不重叠的区间。我们这里使用 C++ 的 Lambda，结合 std::sort() 函数进行自定义排
序

实现代码为

class Solution {
public:
    int eraseOverlapIntervals(vector<vector<int>>& intervals) {
        if(intervals.empty()){
            return 0;
        }
        int n= intervals.size();
        sort(intervals.begin(),intervals.end(),[](vector<int> a,vector<int> b){
            return a[1] < b[1];
        });

        int total =0,prev = intervals[0][1];
        for(int i=1;i<n;++i){
            if(intervals[i][0] < prev){
                ++total;
            }else{
                prev = intervals[i][1];
            }
        }
        return total;
    }
};

605. 种花问题

题目链接

假设有一个很长的花坛，一部分地块种植了花，另一部分却没有。可是，花不能种植在相邻的地块上，它们会争夺水源，两者都会死去。

给你一个整数数组 flowerbed 表示花坛，由若干 0 和 1 组成，其中 0 表示没种植花，1 表示种植了花。另有一个数 n ，能否在不打破种植规则的情况下种入 n 朵花？能则返回 true ，不能则返回 false。

示例 1：

输入：flowerbed = [1,0,0,0,1], n = 1
输出：true
示例 2：

输入：flowerbed = [1,0,0,0,1], n = 2
输出：false

提示：

1 <= flowerbed.length <= 2 * 104
flowerbed[i] 为 0 或 1
flowerbed 中不存在相邻的两朵花
0 <= n <= flowerbed.length

解题思路

贪心算法：从左向右遍历花坛，在可以种花的位置就种一朵，能种就种（因为在任一种花时候，不种都不会得到更优解），是一种贪心的思想。

对于当前遍历的位置，这个位置是否能种上花，必须满足以下条件：

当前位置 flowerbed[i] = 0flowerbed[i]=0 + 当前这个位置是数组末尾 i == flowerbed.length - 1i==flowerbed.length−1 + 前一个位置上没有种花 flowerbed[i - 1] = 0flowerbed[i−1]=0，此时可以在该位置种花。

当前位置 flowerbed[i] = 0flowerbed[i]=0 + 当前这个位置后一个位置没有种花 flowerbed[i + 1] = 0flowerbed[i+1]=0 + 当前这个位置是数组的开头 i == 0i==0，此时可以在该位置种花。

当前位置 flowerbed[i] = 0flowerbed[i]=0 + 当前这个位置后一个位置没有种花 flowerbed[i + 1] = 0flowerbed[i+1]=0 + 前一个位置上没有种花 flowerbed[i - 1] = 0flowerbed[i−1]=0，此时可以在该位置种花。

当前位置 flowerbed[i] = 0flowerbed[i]=0 并且只有这一个位置，即 i == flowerbed.length - 1iflowerbed.length−1 并且 i == 0i0，此时可以在该位置种花。

代码如下

class Solution {

    public boolean canPlaceFlowers(int[] flowerbed, int n) {

        int m = flowerbed.length;
        
        int count = 0;
        for (int i=0;i<m;i++) {

            if (flowerbed[i] == 0 && (i == m - 1 || flowerbed[i + 1] == 0) && (i == 0 || flowerbed[i - 1] == 0)) {

                flowerbed[i] = 1;
                count++;
            }
        }
        return count >= n;
    }
}

但其实还有更加简便的方法

在 flowerbed 数组两端各增加一个 0， 这样处理的好处在于不用考虑边界条件，任意位置处只要连续出现三个 0 就可以栽上一棵花。

下面是我写的代码

class Solution {
public:
    bool canPlaceFlowers(vector<int>& flowerbed, int n) {
       
        flowerbed.insert(flowerbed.begin(),0);
        flowerbed.push_back(0);
        int len = flowerbed.size();
        for(int i=1;i<len-1;i++){
            if(flowerbed[i-1]==0&&flowerbed[i]==0&&flowerbed[i+1]==0){
                flowerbed[i] =1;
                n -= 1;
            }
        }
        return n<=0;
    }
};

452. 用最少数量的箭引爆气球

题目链接

思路
如何使用最少的弓箭呢？

直觉上来看，貌似只射重叠最多的气球，用的弓箭一定最少，那么有没有当前重叠了三个气球，我射两个，留下一个和后面的一起射这样弓箭用的更少的情况呢？

尝试一下举反例，发现没有这种情况。因为都需要两支箭

那么就试一试贪心吧！局部最优：当气球出现重叠，一起射，所用弓箭最少。全局最优：把所有气球射爆所用弓箭最少。

算法确定下来了，那么如何模拟气球射爆的过程呢？是在数组中移除元素还是做标记呢？

如果真实的模拟射气球的过程，应该射一个，气球数组就remove一个元素，这样最直观，毕竟气球被射了。

但仔细思考一下就发现：如果把气球排序之后，从前到后遍历气球，被射过的气球仅仅跳过就行了，没有必要让气球数组remote气球，只要记录一下箭的数量就可以了。

以上为思考过程，已经确定下来使用贪心了，那么开始解题。

为了让气球尽可能的重叠，需要对数组进行排序。

那么按照气球起始位置排序，还是按照气球终止位置排序呢？

其实都可以！只不过对应的遍历顺序不同，我就按照气球的起始位置排序了。

既然按照起始位置排序，那么就从前向后遍历气球数组，靠左尽可能让气球重复。

从前向后遍历遇到重叠的气球了怎么办？

如果气球重叠了，重叠气球中右边边界的最小值 之前的区间一定需要一个弓箭。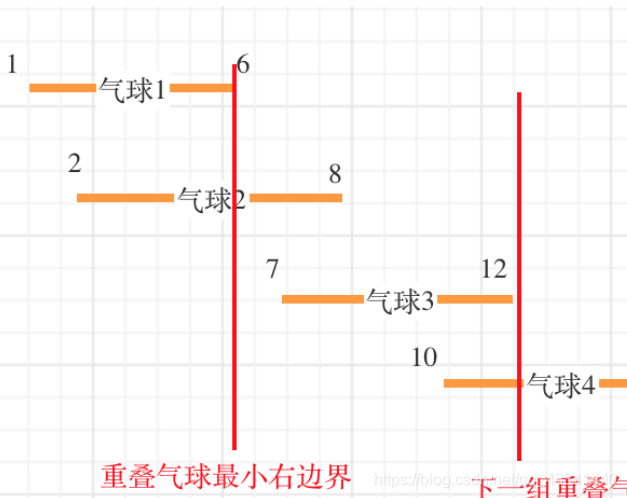

如图，气球三虽然与气球2重叠了，但是因为它的左边界大于前面一组的最小右边界，因此不能一起射穿
因此在算法实现的过程中，如果发现有气球重叠，就需要更新这一组气球的最小右边界

参考：https://leetcode-cn.com/problems/minimum-number-of-arrows-to-burst-balloons/solution/dai-ma-sui-xiang-lu-dai-ni-xue-tou-tan-x-5wfl/

代码实现

class Solution {
public:
	
	int findMinArrowShots(vector<vector<int>>& points) {
		if (points.size() == 0) {
			return 0;
		}

		sort(points.begin(), points.end(), [](vector<int> a, vector<int> b) {
			return a[0] < b[0];
			});

		int len = points.size();
		
		int res = 1;// 因为气球不为空，所以至少需要一支箭

		for (int i = 1; i < len; i++) {
			// 如果不重合
			if (points[i][0] > points[i - 1][1]) {
				res++;
			}
			else {
				// 如果重和，更新最小右边界
				points[i][1] = min(points[i - 1][1], points[i][1]);
			}
		}
		return res;
	}
};

总结

先发布一版，后续还有一期，这期的题目难度，简单，中等，困难都有，可以感受到，有时候贪心算法思路很简单，但是实现起来，是需要很多小技巧的，这些技巧，只有通过不断的练习，才能掌握！