题目链接:
给定二叉搜索树(BST)的根节点和要插入树中的值,将值插入二叉搜索树。 返回插入后二叉搜索树的根节点。 输入数据 保证 ,新值和原始二叉搜索树中的任意节点值都不同。
注意,可能存在多种有效的插入方式,只要树在插入后仍保持为二叉搜索树即可。 你可以返回 任意有效的结果
示例 1:
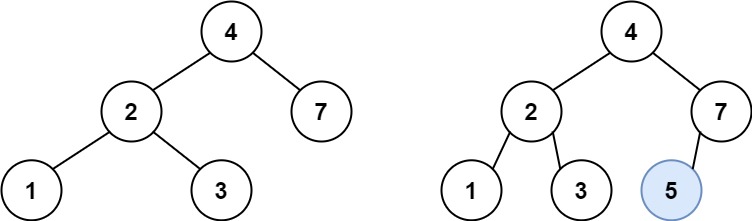
输入:root = [4,2,7,1,3], val = 5
输出:[4,2,7,1,3,5]
解释:另一个满足题目要求可以通过的树是:
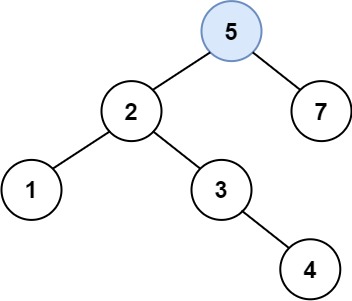
示例 2:
输入:root = [40,20,60,10,30,50,70], val = 25
输出:[40,20,60,10,30,50,70,null,null,25]
示例 3:
输入:root = [4,2,7,1,3,null,null,null,null,null,null], val = 5
输出:[4,2,7,1,3,5]
提示:
-
给定的树上的节点数介于
0和10^4之间 -
每个节点都有一个唯一整数值,取值范围从
0到10^8 -
-10^8 <= val <= 10^8 -
新值和原始二叉搜索树中的任意节点值都不同
解题思路
这道题不考虑题目中说的另一种重构树的插入方式就会变得简单很多。因此我们就利用二叉搜索树的规则去遍历,遇到空节点再将新节点插入就可以了。
递归
这里利用了函数的返回值完成新节点与其父节点的赋值操作。
C++
//递归 class Solution { public: TreeNode* insertIntoBST(TreeNode* root, int val) { if (root == nullptr) { TreeNode* node = new TreeNode(val); return node; } if (val < root->val) { TreeNode* leftNode = insertIntoBST(root->left, val); root->left = leftNode; } if (val > root->val) { TreeNode* rightNode = insertIntoBST(root->right, val); root->right = rightNode; } return root; } };
JavaScript
/** * 递归 * @param {TreeNode} root * @param {number} val * @return {TreeNode} */ var insertIntoBST = function(root, val) { if (root === null) { let node = new TreeNode(val); return node; } if (val < root.val) root.left = insertIntoBST(root.left, val); if (val > root.val) root.right = insertIntoBST(root.right, val); return root; };
迭代
这里利用 pre 来记录当前节点的前一个节点。
C++
//迭代 class Solution1 { public: TreeNode* insertIntoBST(TreeNode* root, int val) { if (root == nullptr) { TreeNode* node = new TreeNode(val); return node; } TreeNode* cur = root; TreeNode* pre = nullptr; while (cur) { pre = cur; if (val < cur->val) cur = cur->left; else if (val > cur->val) cur = cur->right; } cur = new TreeNode(val); if (cur->val < pre->val) pre->left = cur; else if (cur->val > pre->val) pre->right = cur; return root; } };
JavaScript
/** * 迭代 * @param {TreeNode} root * @param {number} val * @return {TreeNode} */ var insertIntoBST = function(root, val) { if (root === null) { let node = new TreeNode(val); return node; } let cur = root; let pre = null; while (cur) { pre = cur; if (val < cur.val) cur = cur.left; else if (val > cur.val) cur = cur.right; } cur = new TreeNode(val); if (cur.val < pre.val) pre.left = cur; else if (cur.val > pre.val) pre.right = cur; return root; };