广度优先搜索(breadth-first search -- BFS)
广度优先搜索又叫做 宽度优先搜索,其英文缩写为BFS,是我们在解决图类问题和树上问题的一个很好的解决算法。
BFS通常帮助我们解决一类最优问题: 距离最短,次数最少,时间最短等...以及连通块等图问题
如果你前面认真学习了深度优先搜索的话,你会发现深度优先搜索的特性是搜索出每一个可能结果将所有结果汇总进行比较最终得出最优解。这样对于常数很小的问题 深度优先搜索可以起到很好的作用,但是如果对于常数很大的问题,我们会发现此时我们在使用dfs会出现超时的情况(TLE), 这个时候就需要引入我们的广度优先搜索了,广度优先搜索可以有效的解决此类求解最优解问题。
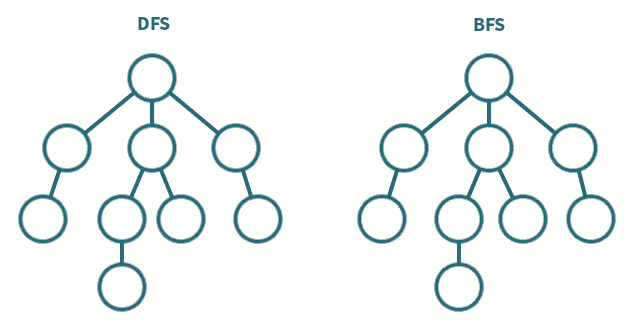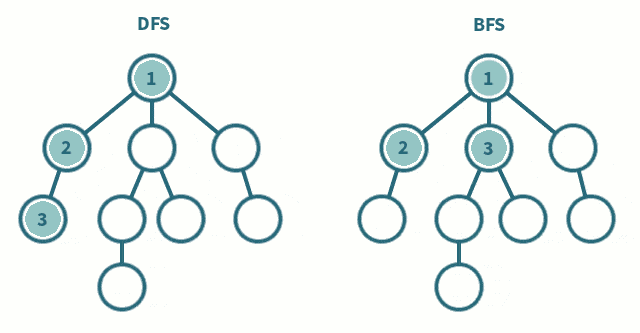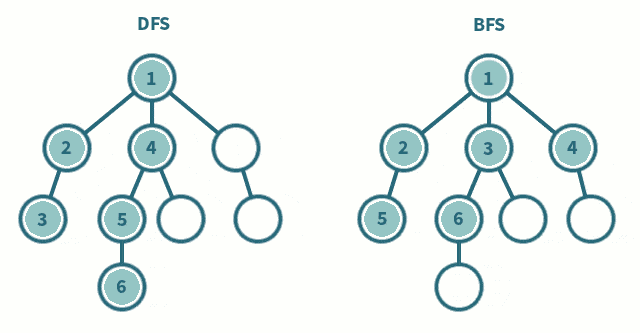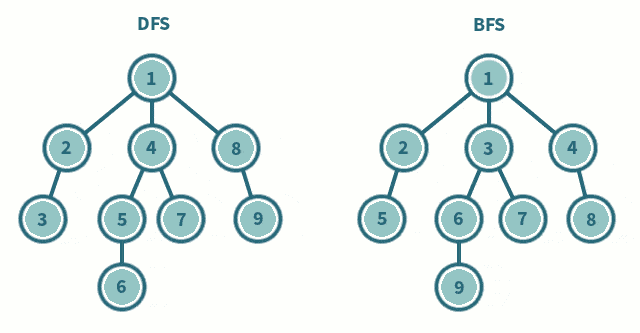
在我们学习广度优先搜索之前我们需要先学习一种数据结构: 队列
队列(queue)
队列的基本概念
队列是一种特殊的线性表,特殊之处在于它只允许在表的前端(front)进行删除操作,而在表的后端(rear)进行插入操作,和栈一样,队列是一种操作受限制的线性表。进行插入操作的端称为队尾,进行删除操作的端称为队头。队列中没有元素时,称为空队列。
队列的数据元素又称为队列元素。在队列中插入一个队列元素称为入队,从队列中删除一个队列元素称为出队。因为队列只允许在一端插入,在另一端删除,所以只有最早进入队列的元素才能最先从队列中删除,故队列又称为先进先出(FIFO—first in first out)(先来先服务)线性表。
大家可以把队列这种数据结构想像称为我们在食堂排队打饭 hh,排在前面的优先打上饭,而排在后面要等前面人都打上饭才能去打饭

上面这个过程就体现了队列的出队过程
如果你来晚了也想去吃饭,那么你只能从队列的尾巴开始排队,这就是队列的入队过程
大家暂时可以不用在意这些数据结构是怎么实现的,因为这部分内容之后上数据结构课程时会学到,我们现在只需要知道队列在C++ / Java语言中怎么使用即可
C++ 中的队列使用
#include <iostream>
#include <queue>// 引入队列头文件
using namespace std;
int main()
{
// 创建一个队列 指定类型
queue<int> q;
// 往队列中添加元素
q.push(1);
q.push(2);
q.push(3);
// 出队
while(!q.empty())
{
// 取出队首
int first = q.front();
cout << first << " ";
q.pop();
}
return 0;
}
// 打印结果
1 2 3
Java中队列的使用
import java.util.LinkedList;
import java.util.Queue;
public class queue {
public static void main(String[] args) {
创建队列
Queue<Integer> q = new LinkedList<>();
往队列中添加元素
q.offer(1);
q.offer(2);
q.offer(3);
依次打印栈的元素
while(!q.isEmpty())
{
int first = q.poll();
System.out.println(first);
}
}
}
现在已经知道了队列这种数据结构下面我们学习如何使用队列来进行广度优先搜索
下面我们根据一道例题来学习广度优先搜索的使用
题目传送门
题目描述
有一个n*m的棋盘(1<n,m<=400),在某个点上有一个马,要求你计算出马到达棋盘上任意一个点最少要走几步
输入格式
一行四个数据,棋盘的大小和马的坐标
输出格式
一个n*m的矩阵,代表马到达某个点最少要走几步(左对齐,宽5格,不能到达则输出-1)
输入输出样例
输入 #1
3 3 1 1
输出 #1
0 3 2
3 -1 1
2 1 4
分析:
首先我们读题发现题目让我们求得是最少步数,那么我们优先使用广度优先搜索(在这里对比一下两种搜索)。
根据样例信息我们可以得到如下所示图:
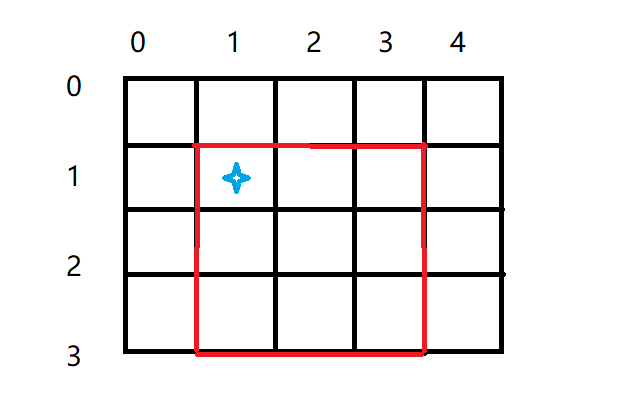
题目中说得是马得行走方式,那么马走日这个规矩相信我就不用多说了吧,马走一步可以到达图上哪些点呢?
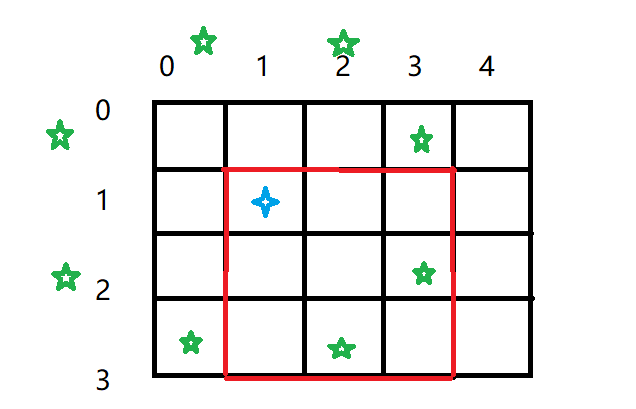
图中绿色得地方就代表马可以跳的得地方。怎么样才能够得出这些坐标呢 大家自己仔细想一下。
我们已经知道了马一次可以跳到得点那么我们可以根据跳到得位置在来到下一次能跳得位置,然后不断重复这个过程就可以得到每一个可以走过得位置。
而且我们会发现我们第一次走过得位置就是到达该位置得最小步数,因为我们一次只走了一步。详情听视频分解
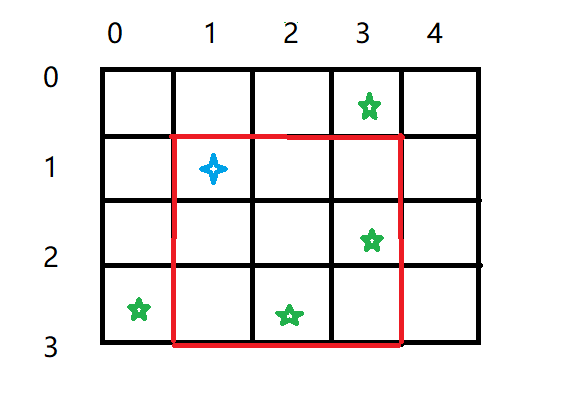
详细得广搜过程带着大家写一遍代码体会,注意看视频。
代码过程
#include <iostream>
#include <algorithm>
#include <cstdio>
#include <cmath>
#include <queue>
using namespace std;
int n, m;
int map[401][401];
bool vis[401][401];
int _next[8][2] = { { -2, -1 }, { -2, 1 }, { -1, -2 }, { -1, 2 }, { 1, 2 }, { 1, -2 }, { 2, 1 }, { 2, -1 } };;
typedef struct node {
int x, y;
}N;
bool inmap(N a)
{
return (a.x >= 1 && a.x <= n && a.y >= 1 && a.y <= m);
}
void outans()
{
for (int i = 1; i <= n; i++)
{
for (int j = 1; j <= m; j++)
{
printf("%-5d", map[i][j]);
}
cout << endl;
}
}
void bfs(N start)
{
queue<N> q;
map[start.x][start.y] = 0;
vis[start.x][start.y] = 1;
q.push(start);
while (!q.empty())
{
N now = q.front();
for (int i = 0; i < 8; i++)
{
N tmp;
tmp.x = _next[i][0] + now.x;
tmp.y = _next[i][1] + now.y;
if (inmap(tmp) == true && vis[tmp.x][tmp.y] == 0)
{
vis[tmp.x][tmp.y] = 1;
map[tmp.x][tmp.y] = map[now.x][now.y] + 1;
q.push(tmp);
}
}
q.pop();
}
outans();
}
void init()
{
N s;
fill(map[0], map[0]+ 401*401, -1);
cin >> n >> m >> s.x >> s.y;
bfs(s);
}
int main()
{
init();
system("pause");
return 0;
}