Here is a square matrix of n * nn∗n, each lattice has its value (nn must be odd), and the center value is n * nn∗n. Its spiral decline along the center of the square matrix (the way of spiral decline is shown in the following figure:)
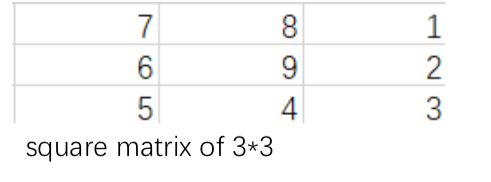

The grid in the lower left corner is (1,1) and the grid in the upper right corner is (n , n)
Now I can choose mm squares to build palaces, The beauty of each palace is equal to the digital sum of the value of the land which it is located. Such as (the land value is 123213123213,the beautiful values of the palace located on it is 1+2+3+2+1+3=121+2+3+2+1+3=12) (666666 -> 1818) (456456 ->1515)
Next, we ask pp times to the sum of the beautiful values of the palace in the matrix where the lower left grid(x_1,y_1x1,y1), the upper right square (x_2,y_2x2,y2).
Input
The first line has only one number TT .Representing TT-group of test data (Tle 5)(T≤5)
The next line is three number: n m pn m p
The mm lines follow, each line contains two integers the square of the palace (x, y )(x,y)
The pp lines follow, each line contains four integers : the lower left grid (x_1,y_1)(x1,y1) the upper right square (x_2,y_2)(x2,y2)
Output
Next, p_1+p_2...+p_Tp1+p2...+pT lines: Represent the answer in turn(n le 10^6)(m , p le 10^5)(n≤106)(m,p≤105)
样例输入
1 3 4 4 1 1 2 2 3 3 2 3 1 1 1 1 2 2 3 3 1 1 3 3 1 2 2 3
样例输出
5 18 23 17
思路:
题目的意思是给你一个n*n的矩阵 但是n很大 我们显然不能用前缀和数组来维护 但是考虑到点只有1e6个 所以我们可以用树状数组来维护y轴 那么这个其实是经典的二维偏序问题 最后我们要解决的其实就是螺旋矩阵的映射问题 对于(i,j)O(1)求出对应的权值:
一种思路是求圈数k 然后k圈的第一个权值:F(k)=F(k-1)+4*(n-1-2*(k-1))
我们可以推出递推式 F(k)=1+4*(k-1)*(n-k+1)
最后下右和左上分别讨论一下即可

#include <bits/stdc++.h> using namespace std; typedef long long ll; const int N = 1e6+7; struct node{ ll x,y,v,id; friend bool operator < (node a,node b){ if(a.x!=b.x) return a.x<b.x; if(a.y!=b.y) return a.y<b.y; return a.id<b.id; } }p[N]; ll getv(ll x,ll y,ll n){ ll t=min(x,min(y,min(n-y+1,n-x+1))); ll res=1+4*(t-1)*(n-t+1); ll ans; if(x>=y) ans=res+2*(n-t+1)-x-y; else ans=res+2*(n-2*(t-1)-1)+x+y-2*t; ll xx=0; while(ans){ xx+=(ans%10); ans/=10; } return xx; } ll C[N]; ll lowbit(ll x){ return x&(-x); } void add(ll x,ll v){ while(x<=N){ C[x]+=v; x+=lowbit(x); } } ll ask(ll x){ ll ans=0; while(x){ ans+=C[x]; x-=lowbit(x); } return ans; } ll ans[N]; int main(){ int t; scanf("%d",&t); while(t--){ memset(C,0,sizeof(C)); memset(ans,0,sizeof(ans)); ll n,m,pp; scanf("%lld%lld%lld",&n,&m,&pp); for(int i=0;i<m;i++){ ll x,y; scanf("%lld%lld",&x,&y); p[i].x=x; p[i].y=y; p[i].v=getv(x,y,n); p[i].id=0; } int cnt=m-1; for(int i=1;i<=pp;i++){ ll x1,y1,x2,y2; scanf("%lld%lld%lld%lld",&x1,&y1,&x2,&y2); ++cnt; p[cnt].x=x1-1; p[cnt].y=y1-1; p[cnt].v=1; p[cnt].id=i; ++cnt; p[cnt].x=x2; p[cnt].y=y2; p[cnt].v=1; p[cnt].id=i; ++cnt; p[cnt].x=x1-1; p[cnt].y=y2; p[cnt].v=0; p[cnt].id=i; ++cnt; p[cnt].x=x2; p[cnt].y=y1-1; p[cnt].v=0; p[cnt].id=i; } sort(p,p+cnt+1); for(int i=0;i<=cnt;i++){ if(p[i].id){ if(p[i].v==1) ans[p[i].id]+=ask(p[i].y); else ans[p[i].id]-=ask(p[i].y); }else{ add(p[i].y,p[i].v); } } for(int i=1;i<=pp;i++){ printf("%lld ",ans[i]); } } }
