Dijkstra And Floyd C++

一.Dijkstra 算法

//在这里采用两种方式实现Dijkstra算法，经过测试两种方式：第一种：通过Dist【】让每一个顶点中Dist[]中寻找最短路径的点；第二种方式：从已经收录的顶点的相邻顶点中选择出最短路//径的的顶点，此种方式适合用于稠密图，减少点的遍历。


#include<iostream>
 #include<malloc.h>
 using namespace std;
 #define INF (100000)

 //相连顶点的信息
 typedef struct AdjNode{
    int Weight;
    int CostValue;
    int Adj;
    AdjNode *next;
AdjNode():Weight(NULL),CostValue(NULL),next(NULL){};
 }PtrToAdjVNode;

 //表头信息,每个表头的节点必须要进行标记，对表头进行标记
 typedef struct Vnode{
     PtrToAdjVNode *FirstEdge;
     int Flag;
 }AdjLink[10];

 typedef struct AdjGraph{
 int VerterNum;
 int EdgeNum;
 AdjLink LG;
 }LGraph;

 LGraph *Graph=new LGraph;
 void Insert(int A,int B,int C,int D)
 {
    PtrToAdjVNode *Ptr=new PtrToAdjVNode,*Rear;
    Ptr->Adj=B;
    Ptr->Weight=C;Ptr->CostValue=D;Ptr->next=NULL;
    if(!Graph->LG[A].FirstEdge)
    {
        Graph->LG[A].FirstEdge=Ptr;
    }
    else
    {
        Rear=Graph->LG[A].FirstEdge;
        while(Rear->next!=NULL)
        {
            Rear=Rear->next;
        }
        Rear->next=Ptr;
    }
 }
void CreateGraph(int VerNum,int EdgeNum)
 {//顶点从0开始
     int i;Graph->VerterNum=VerNum;Graph->EdgeNum=EdgeNum;
         for(i=0;i<VerNum;i++)
         {
             Graph->LG[i].Flag=NULL;
             Graph->LG[i].FirstEdge=NULL;
         }
         int NN,MM,KK,CC;
         for(i=0;i<EdgeNum;i++)
         {
            cin>>NN>>MM>>KK>>CC;
            Insert(NN,MM,KK,CC);
         }
 }


 int Get_Weight(int Start,int FindNum)
 {
     PtrToAdjVNode *Rear=Graph->LG[Start].FirstEdge;
     int Value=INF;
     if(Start==FindNum)
         return 0;
     while(Rear)
     {
         if(Rear->Adj==FindNum)
             
             {   
                        Value=Rear->Weight;
                        break;
            }
         else
         {
             Rear=Rear->next;
         }

     }
     return Value;
 }
 void Search(int prev[],int Start,int end)
 {
    //简单摆Dijkstra算法遍历
     int i=end,j=0;int *rev=new int[Graph->VerterNum];
     //倒序的路径
     for(i=end;i!=Start;i=prev[i])
     {
        cout<<"["<<i<<"] ";
        rev[j++]=i;
     }
     cout<<i<<endl;
 }

 void Dijkstra(int dist1[],int prev1[],int Vstart,int Vend)
 {
    //防止出现两条相等路径，最外面只将从Start---End点上的最短路径上顶点在表头上标记
     //最外面只标记最短路径,最好只标记与顶点相邻的分叉点
     /***第一步计算出S点与相邻点的dist,同时初始化*/
     int prev[10],dist[10],flag[10];
     int i;//int *flag=new int[Graph->VerterNum];
     for(i=0;i<Graph->VerterNum;i++)
     {
        
        flag[i]=0;
        dist[i]=Get_Weight(Vstart,i);//只能够得到他么最短路径
        if(dist[i]<INF)
            prev[i]=Vstart;
        else
            prev[i]=-1;
     }
     //接下来是Dijkstra 核心，从U集合中选取一个最短路径的点加入S集合
     //同时更新比较经过k 点与不经过K点到k 的相邻点上距离。

     prev[Vstart]=Vstart;flag[Vstart]=1;
     int m,n,kIndex,j;
     int MIndex=Vstart;
     int Min,Tmp; int Min1=INF,K1;

     for(m=0;m<Graph->VerterNum;m++)//大循环保证每个点都能遍历
     {
         Min=INF;Min1=INF;
        //从U中挑选出离S集合最近的点,通过比较,将各个顶点与S中点相比较
         for(n=0;n<Graph->VerterNum;n++)
         {
             //从没有遍历的点中找到最短路径的点
             
             if(Graph->LG[n].FirstEdge &&Graph->LG[n].Flag==false && !flag[n] )
             {
                 if(dist[n]<Min)
                 {
                     Min=dist[n];
                     kIndex=n;
                 }
             }
         }
         /**上面步骤主要是从相近点中找到最短路径的点,dist存储各个点情况，只有路径就可以到达，保证找到最终点*/
         //如果找到最终点刚好在最短路径上，可以用之下方法
         //只从点的相邻点中找路径，flag表示已经遍历dist存储各个点情况
         PtrToAdjVNode *Rear=Graph->LG[MIndex].FirstEdge; //从相邻点中找最短路径，保证最终点在路径上，但是找出图中最短的点
         while(Rear)
         {
             if(flag[Rear->Adj]==0)
             {
                 if(dist[Rear->Adj]<Min1)
                 {
                     Min1=dist[Rear->Adj];
                     MIndex=Rear->Adj;
                 }
             }
             Rear=Rear->next;
         }
          flag[MIndex]=1;
        
         //不断更新dist同prev
        for(j=0;j<Graph->VerterNum;j++)
        {
            Tmp=Get_Weight(MIndex,j);
            
                Tmp=(Tmp==INF)?INF:(Min1+Tmp);
            
                if(!flag[j] && Graph->LG[j].Flag==false && dist[j]>Tmp)//只有在修改时候才能进行prev修改
                {    dist[j]=Tmp;
                    prev[j]=MIndex;
                }
            }
        
        }
     //对路径的回溯
     Search(prev,Vstart,Vend);

         }
    
 
 int main()
 {
    int VerNum,EdgeNum,VerStart,Verend;
    cin>>VerNum>>EdgeNum>>VerStart>>Verend;
    CreateGraph(VerNum,EdgeNum);

    //选择出最短路径，如果有相同最短路径在计算出最小花费
    int *dist=new int[VerNum]; int *prev=new int[VerNum];
    Dijkstra(dist,prev,VerStart,Verend);
 return 0;
 }

 

Dijkstra算法主要是单源路径的最短算法，计算的是起始点到其他顶点的最短路径；算法具体：

1.S集合中表示收录的最短路径的点集合，U剩余点的集合，Dist[]表示起始点到其他点最短路径，每一次从dist中选择出最短路径的点e（这种方式能够选出多条路径）；

2.对dist和prev矩阵通过新加入的点进行更新。

现在只是解决了最短路径的问题，单路径中出现相等路径怎么用Dijkstra算法计算出相同不同顶点有相同路径算法。

下面这个算法针对计算多条路径：方法，在表头列表中增加一项Prev，记录遍历整个的过程，特别记录到达某点时候dist[i]=Tmp 处值，在这里最有可能会发生相同路径的特需点

模拟图

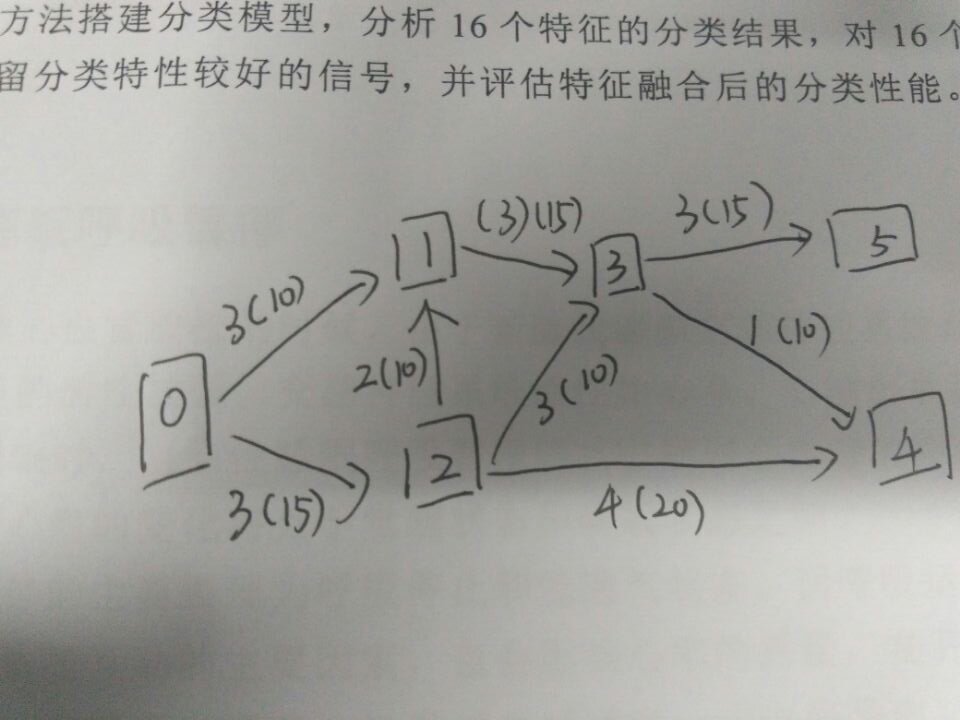
在列表prev中贮存Start到此点中最短路径的前一个点

#include<iostream>
 #include<malloc.h>
 using namespace std;
 #define INF (100000)

 //相连顶点的信息
 typedef struct AdjNode{
    int Weight;
    int CostValue;
    int Adj;
    AdjNode *next;
AdjNode():Weight(NULL),CostValue(NULL),next(NULL){};
 }PtrToAdjVNode;

 //表头信息,每个表头的节点必须要进行标记，对表头进行标记
 typedef struct Vnode{
     PtrToAdjVNode *FirstEdge;
     int prev[5];//记录与此节点距离最近的父节点
     int pcnt;
 }AdjLink[10];

 typedef struct AdjGraph{
 int VerterNum;
 int EdgeNum;
 AdjLink LG;
 }LGraph;

 LGraph *Graph=new LGraph;
 void Insert(int A,int B,int C,int D)
 {
    PtrToAdjVNode *Ptr=new PtrToAdjVNode,*Rear;
    Ptr->Adj=B;
    Ptr->Weight=C;Ptr->CostValue=D;Ptr->next=NULL;
    if(!Graph->LG[A].FirstEdge)
    {
        Graph->LG[A].FirstEdge=Ptr;
    }
    else
    {
        Rear=Graph->LG[A].FirstEdge;
        while(Rear->next!=NULL)
        {
            Rear=Rear->next;
        }
        Rear->next=Ptr;
    }
 }
void CreateGraph(int VerNum,int EdgeNum)
 {//顶点从0开始
     int i;Graph->VerterNum=VerNum;Graph->EdgeNum=EdgeNum;
         for(i=0;i<VerNum;i++)
         {
             Graph->LG[i].pcnt=NULL;
             Graph->LG[i].FirstEdge=NULL;
             memset(Graph->LG[i].prev,-1,sizeof(int)*5);
         }
         int NN,MM,KK,CC;
         for(i=0;i<EdgeNum;i++)
         {
            cin>>NN>>MM>>KK>>CC;
            Insert(NN,MM,KK,CC);
         }
 }


 int Get_Weight(int Start,int FindNum)
 {
     PtrToAdjVNode *Rear=Graph->LG[Start].FirstEdge;
     int Value=INF;
     if(Start==FindNum)
         return 0;
     while(Rear)
     {
         if(Rear->Adj==FindNum)
             
             {   
                        Value=Rear->Weight;
                        break;
            }
         else
         {
             Rear=Rear->next;
         }

     }
     return Value;
 }
 void Search(int prev[],int Start,int end)
 {
    //简单摆Dijkstra算法遍历
     int i=end,j=0;int *rev=new int[Graph->VerterNum];
     //倒序的路径
     for(i=end;i!=Start;i=prev[i])
     {
        cout<<"["<<i<<"] ";
        rev[j++]=i;
     }
    cout<<"["<<i<<"] ";
    rev[j]=Start;
    
    int pathCost=0;
    PtrToAdjVNode *Rear;int K=1;
    while(j>0)
    {
        Rear=Graph->LG[rev[j]].FirstEdge;
        
        if(Rear->next && K)
        {//防止出现双等路径，只标记第一个路径上，这种方式不行的
            //Graph->LG[rev[j]].Flag=true;
            K=0;

        }

        while(Rear)
        {
            if(rev[j-1]==Rear->Adj)
            {    
                pathCost+=Rear->CostValue;
                break;
            }
            else
            {    
                Rear=Rear->next;
            }
        }
        j=j-1;
    }
    cout<<"最短路径上花费"<<pathCost<<endl;

 }
 int Calculate(int A,int B)
 {//计算出两个地图之间花费
     PtrToAdjVNode *Rear=Graph->LG[A].FirstEdge;
     int SiglePath=0;
    while(Rear)
    {
        if(B==Rear->Adj)
            {    
                SiglePath=Rear->CostValue;
                break;
            }
            else
            {    
                Rear=Rear->next;
            }
    }
    return SiglePath;
 }
 void PathCost(int start,int end)
 {
 //多条相等路径，比较相同同时对其进行
     int Trarget=end,Trarget1;
     int *path=new int[Graph->VerterNum];
     int i=0;int cost=0;
     while (Trarget!=start)
     {  
         path[i++]=Trarget;
         if(Graph->LG[Trarget].pcnt==1)
         {
             
             Trarget1=Graph->LG[Trarget].prev[0];
             cost+=Calculate(Graph->LG[Trarget].prev[0],Trarget);
             Trarget=Trarget1;
         }
         else
         {
             //从一系列相等的之中挑选出最小花费路径
            // path[i++]=Trarget;
             int MinINf=INF,Tp;
             for(int j=0;j<Graph->LG[Trarget].pcnt;j++)
             {
                 Tp=Calculate(Graph->LG[Trarget].prev[j],Trarget);
                 if(Tp<MinINf)
                 {
                    MinINf=Tp;
                    
                    Trarget1=Graph->LG[Trarget].prev[j];
                 }
             }
             cost+=MinINf;
             Trarget=Trarget1;
         }
        
     }
     path[i]=start;
     cout<<"多条相等路径中花费最小前："<<cost<<endl;
     for(;i>=0;i--)
     {
     cout<<"["<<path[i]<<"] ";
     }

     
 }
 void Dijkstra(int dist1[],int prev1[],int Vstart,int Vend)
 {
    //防止出现两条相等路径，最外面只将从Start---End点上的最短路径上顶点在表头上标记
     //最外面只标记最短路径,最好只标记与顶点相邻的分叉点
     /***第一步计算出S点与相邻点的dist,同时初始化*/
     int prev[10],dist[10],flag[10];
     int i;//int *flag=new int[Graph->VerterNum];
     for(i=0;i<Graph->VerterNum;i++)
     {
        
        flag[i]=0;
        dist[i]=Get_Weight(Vstart,i);//只能够得到他么最短路径
        if(dist[i]<INF)
        {    prev[i]=Vstart;
        Graph->LG[i].prev[Graph->LG[i].pcnt++]=Vstart;
         }
        else
            prev[i]=-1;
     }
     //接下来是Dijkstra 核心，从U集合中选取一个最短路径的点加入S集合
     //同时更新比较经过k 点与不经过K点到k 的相邻点上距离。

     prev[Vstart]=Vstart;flag[Vstart]=1;
     int m,n,kIndex,j;
     int MIndex=Vstart;
     int Min,Tmp; int Min1=INF,K1;

     for(m=0;m<Graph->VerterNum;m++)//大循环保证每个点都能遍历
     {
         Min=INF;Min1=INF;
        //从U中挑选出离S集合最近的点,通过比较,将各个顶点与S中点相比较
         for(n=0;n<Graph->VerterNum;n++)
         {
             //从没有遍历的点中找到最短路径的点，使用最小堆的方式，每一次的时候可以从最小堆中抛出dist中最短路径，减少运算
             
             if(Graph->LG[n].FirstEdge  && !flag[n] )
             {
                 if(dist[n]<Min)
                 {
                     Min=dist[n];
                     kIndex=n;
                 }
             }
         }
         /**上面步骤主要是从相近点中找到最短路径的点,dist存储各个点情况，只有路径就可以到达，保证找到最终点*/
         //如果找到最终点刚好在最短路径上，可以用之下方法
         //只从点的相邻点中找路径，flag表示已经遍历dist存储各个点情况
         PtrToAdjVNode *Rear=Graph->LG[MIndex].FirstEdge; //从相邻点中找最短路径，保证最终点在路径上，但是找出图中最短的点
         while(Rear)
         {//缺点，如果算多条相等路径，无法计算出来，如果想得出多条路径，判断此点相连的最短路径的点是否有多条。static对其进行储存。这样可以得出多条路径
             if(flag[Rear->Adj]==0)
             {
                 if(dist[Rear->Adj]<Min1)
                 {
                     Min1=dist[Rear->Adj];
                     MIndex=Rear->Adj;
                 }
             }
             Rear=Rear->next;
         }
          flag[kIndex]=1;
        
         //不断更新dist同prev
        for(j=0;j<Graph->VerterNum;j++)
        {
            Tmp=Get_Weight(kIndex,j);
            
                Tmp=(Tmp==INF)?INF:(Min+Tmp);
            
                if(!flag[j]  && dist[j]>Tmp)//只有在修改时候才能进行prev修改
                {    
                    dist[j]=Tmp;
                    prev[j]=kIndex;
                    Graph->LG[j].prev[Graph->LG[j].pcnt++]=kIndex;
                }
                else if(dist[j]==Tmp && dist[j]!=INF && !flag[j] && kIndex!=j)
                {
                    Graph->LG[j].prev[Graph->LG[j].pcnt++]=kIndex;
                    flag[kIndex]=1;
                }
            }
        
        }
     //对路径的回溯

     Search(prev,Vstart,Vend);
     //多条相等的路径存取在头列表中如何对其进行遍历
     PathCost(Vstart,Vend);

         }
    
 
 int main()
 {
    int VerNum,EdgeNum,VerStart,Verend;
    cin>>VerNum>>EdgeNum>>VerStart>>Verend;
    CreateGraph(VerNum,EdgeNum);

    //选择出最短路径，如果有相同最短路径在计算出最小花费
    int *dist=new int[VerNum]; int *prev=new int[VerNum];
        Dijkstra(dist,prev,VerStart,Verend);
 return 0;
 }

 二.Floyed 算法（o(N^3)）在C语言中明显如何发生溢出

多源路径最短算法：