1.算法复杂度与设计的数据结构 有关 设计成有一个数组id,id[] 元素保存其相连接的点的编号值 如下所示,采用这种类型的数据结构图
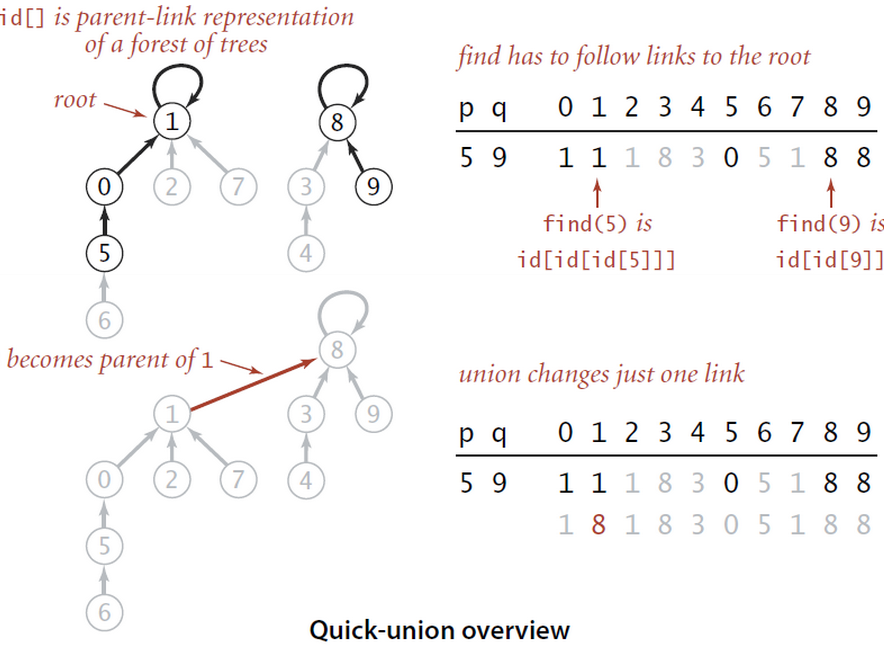
1 public int Find(int p) 2 { 3 //找出分量的名车,寻找分量的根结点值 4 //寻找p节点所在组的根节点,根节点具有性质id[root] = root 5 while(p!=id[p]) 6 p=id[p]; 7 return p; 8 } 9 10 public void union(int p,int q) 11 { 12 // Give p and q the same root 13 int pRoot=Find(p); 14 int qRoot=Find(q); 15 if(pRoot==qRoot) 16 return; 17 id[pRoot]=qRoot; 18 count--; 19 }
对于这种 Union:1. 在树建立过程出,树的最终形态严重依赖于输入数据本身的性质,比如数据是否排序,是否随机分布等等。比如在输入数据是有序的情况下,构造的BST会退化成一个链表。在我们这个问题中,也是会出现的极端情况的
当然采用 红黑树或者二叉搜索树的方式进行区分
2. id[pRoot]=qRoot;出现一种情形让树明显的倾斜,解决这种问题 必须要比较Union时候 树的大小,让较小树连接到较大树上 ---对原有数组进行小修改 用 id[root]=-(树的数量);负号保证找到其是根结点
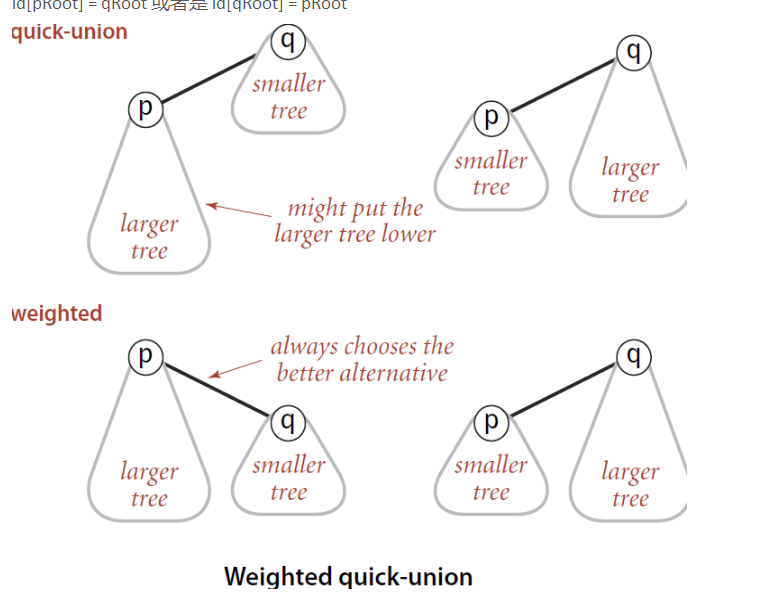
1 public void weight_union(int p,int q) 2 { 3 int pRoot=Find(p); 4 int qRoot=Find(q); 5 if(pRoot==qRoot) 6 return; 7 if(id[pRoot]<id[qRoot]) 8 { 9 id[qRoot]=pRoot; 10 id[pRoot]+=id[qRoot]; 11 } 12 else 13 { 14 id[pRoot]=qRoot; 15 id[qRoot]+=id[pRoot]; 16 } 17 }