数据结构与算法简记--最短路径算法

最短路径算法（Shortest Path Algorithm）

---

 地图寻路最优路径

距离最短

红灯最少

速度最快

建模

使用有向有权图(graph)表示：岔口为顶点，岔口相连为边，单行线建立单向边，双行线建立双向边，岔口之间的距离为边的权重。

• public class Graph { // 有向有权图的邻接表表示
    private LinkedList<Edge> adj[]; // 邻接表
    private int v; // 顶点个数
  
    public Graph(int v) {
      this.v = v;
      this.adj = new LinkedList[v];
      for (int i = 0; i < v; ++i) {
        this.adj[i] = new LinkedList<>();
      }
    }
  
    public void addEdge(int s, int t, int w) { // 添加一条边
      this.adj[s].add(new Edge(s, t, w));
    }
  
    private class Edge {
      public int sid; // 边的起始顶点编号
      public int tid; // 边的终止顶点编号
      public int w; // 权重
      public Edge(int sid, int tid, int w) {
        this.sid = sid;
        this.tid = tid;
        this.w = w;
      }
    }
    // 下面这个类是为了dijkstra实现用的
    private class Vertex {
      public int id; // 顶点编号ID
      public int dist; // 从起始顶点到这个顶点的距离
      public Vertex(int id, int dist) {
        this.id = id;
        this.dist = dist;
      }
    }
  }

经典单源最短路径算法（一个顶点到一个顶点）： Dijkstra 算法

• // 因为Java提供的优先级队列，没有暴露更新数据的接口，所以我们需要重新实现一个
  private class PriorityQueue { // 根据vertex.dist构建小顶堆
    private Vertex[] nodes;
    private int count;
    public PriorityQueue(int v) {
      this.nodes = new Vertex[v+1];
      this.count = v;
    }
    public Vertex poll() { // TODO: 留给读者实现... }
    public void add(Vertex vertex) { // TODO: 留给读者实现...}
    // 更新结点的值，并且从下往上堆化，重新符合堆的定义。时间复杂度O(logn)。
    public void update(Vertex vertex) { // TODO: 留给读者实现...} 
    public boolean isEmpty() { // TODO: 留给读者实现...}
  }
  
  public void dijkstra(int s, int t) { // 从顶点s到顶点t的最短路径
    int[] predecessor = new int[this.v]; // 用来还原最短路径
    Vertex[] vertexes = new Vertex[this.v];
    for (int i = 0; i < this.v; ++i) {
      vertexes[i] = new Vertex(i, Integer.MAX_VALUE);
    }
    PriorityQueue queue = new PriorityQueue(this.v);// 小顶堆
    boolean[] inqueue = new boolean[this.v]; // 标记是否进入过队列
    vertexes[s].dist = 0;
    queue.add(vertexes[s]);
    inqueue[s] = true;
    while (!queue.isEmpty()) {
      Vertex minVertex= queue.poll(); // 取堆顶元素并删除
      if (minVertex.id == t) break; // 最短路径产生了
      for (int i = 0; i < adj[minVertex.id].size(); ++i) {
        Edge e = adj[minVertex.id].get(i); // 取出一条minVetex相连的边
        Vertex nextVertex = vertexes[e.tid]; // minVertex-->nextVertex
        if (minVertex.dist + e.w < nextVertex.dist) { // 更新next的dist
          nextVertex.dist = minVertex.dist + e.w;
          predecessor[nextVertex.id] = minVertex.id;
          if (inqueue[nextVertex.id] == true) {
            queue.update(nextVertex); // 更新队列中的dist值
          } else {
            queue.add(nextVertex);
            inqueue[nextVertex.id] = true;
          }
        }
      }
    }
    // 输出最短路径
    System.out.print(s);
    print(s, t, predecessor);
  }
  
  private void print(int s, int t, int[] predecessor) {
    if (s == t) return;
    print(s, predecessor[t], predecessor);
    System.out.print("->" + t);
  }

• 算法解析
  • 从优先级队列中取出 dist 最小的顶点 minVertex，然后考察这个顶点可达的所有顶点（代码中的 nextVertex）。
  • 如果 minVertex 的 dist 值加上 minVertex 与 nextVertex 之间边的权重 w 小于 nextVertex 当前的 dist 值，也就是说，存在另一条更短的路径，经过 minVertex 到达 nextVertex。那我们就把 nextVertex 的 dist 更新为 minVertex 的 dist 值加上 w。
  • 然后，把 nextVertex 加入到优先级队列中。
  • 重复这个过程，直到找到终止顶点 t 或者队列为空。
  • 两个额外的变量：predecessor 数组和 inqueue 数组
    • predecessor 数组的作用是为了还原最短路径，它记录每个顶点的前驱顶点。通过递归的方式，将这个路径打印出来。
    • inqueue 数组是为了避免将一个顶点多次添加到优先级队列中。更新了某个顶点的 dist 值之后，如果这个顶点已经在优先级队列中了，就不要再将它重复添加进去了。
• 图示
• 
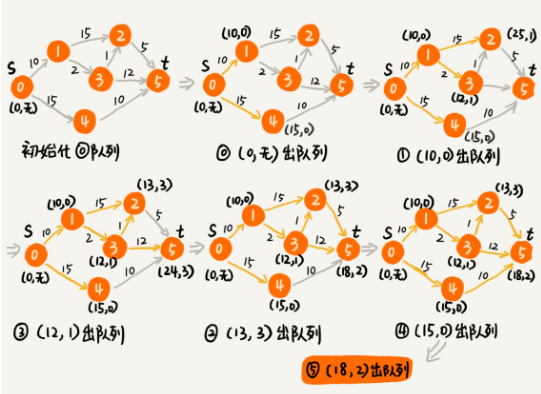
• 时间复杂度：O（V * E）

获取翻译结果高分TOP K

• 借助 Dijkstra 算法的核心思想，高效地解决：
• 每个单词的可选翻译是按照分数从大到小排列的，所以 a0​b0​c0​ 肯定是得分最高组合结果。
• 我们把 a0​b0​c0​ 及得分作为一个对象，放入到优先级队列中。
• 每次从优先级队列中取出一个得分最高的组合，并基于这个组合进行扩展。
• 扩展的策略是每个单词的翻译分别替换成下一个单词的翻译。比如 a0​b0​c0​ 扩展后，会得到三个组合，a1​b0​c0​、a0​b1​c0​、a0​b0​c1​。把扩展之后的组合，加到优先级队列中。
• 重复这个过程，直到获取到 k 个翻译组合或者队列为空。
• 

总结

Dijkstra 算法的核心思想：

确定当前最优结果，基于此结果不断扩展；

使用优先级队列，存储扩展结果；

每次1组堆顶元素出队，n组基于堆顶扩展的结果入队；

达到目标则终止操作，根据最后的出队结果打印路径就是最终结果。