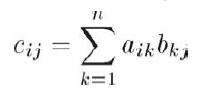矩阵是3D数学的重要基础,它主要用来描述两个坐标系间的关系,通过定义一种运算而将一个坐标系中的向量转换到另一个坐标系中。在线性代数中,矩阵就是以行和列形式组织的矩形数字块,向量是标量的数组,矩阵是向量的数组。
矩阵的维度和记法
矩阵的维度被定义为它包含了多少行多少列,一个 r x c 矩阵有r行c列。用黑体大写字母表示矩阵,如:M、A、R。需要引用矩阵的分量时,采用下标法,常使用对应的斜体小写字母,如下面的3 x 3矩阵所示:
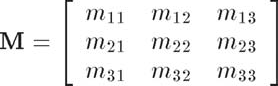
方阵
行数和列数相同的矩阵称作方阵,方阵的对角线元素就是方阵中行号和列号相同的元素。其他元素均为非对角元素,简单的说,方阵的对角元素就是方阵对角线上的元素。
如果所有非对角元素都为0,那么称这种矩阵为对角矩阵。单位矩阵是一种特殊的对角矩阵,n维单位矩阵记作In,是nxn矩阵,对角线元素为1,其他元素为0.
单位矩阵非常特殊,因为它是矩阵的乘法单位元。其基本性质是用任意一个矩阵乘以单位矩阵,都将得到原矩阵。所以在某种意义上,单位矩阵对矩阵的作用就犹如1对于标量的作用。
向量作为矩阵使用
矩阵的行数和列数可以是任意正整数,当然也包括1。一个n维向量能被当作 1 x n 矩阵或 n x 1 矩阵。1 x n 矩阵称作行向量,n x 1 矩阵称作列向量。行向量平着写,列向量竖着写。
转置
考虑一个 r x c 矩阵M,M的转置记作MT,是一个 c x r 矩阵,它的列由M的行组成,可以从另一方面理解,即沿着矩阵的对角线翻折。

对于向量来说,转置将使行向量变成列向量,使列向量成为行向量,见公式7.3:
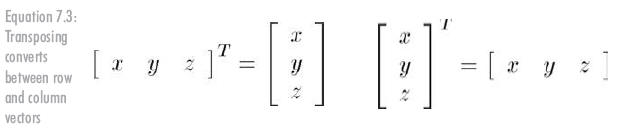
标量和矩阵的乘法
矩阵M能和标量k相乘,结果是一个和M维数相同的矩阵。矩阵和标量相乘的记法如公式7.4所示,标量经常写在左边,不需要写乘号。这种乘法法则很直观,即用k乘以M中的每个元素。
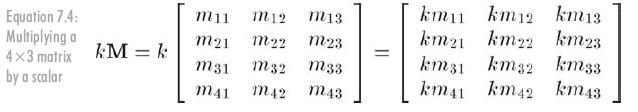
矩阵乘法
某些情况下,两个矩阵能够相乘,决定矩阵能否相乘以及怎样计算结果的法则初看起来有些奇怪。一个r x n矩阵A能够乘以一个n x c矩阵B,结果是一个r x c矩阵,记作AB。
例如,设A为4 x 2矩阵,B为2 x 5矩阵,那么结果AB为4 x 5矩阵:
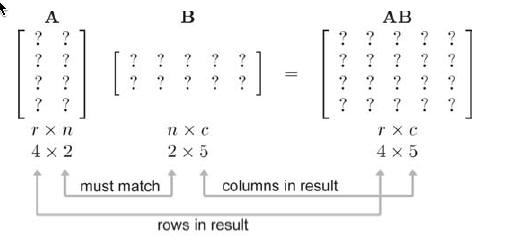
如果矩阵A的列数和B的行数不匹配,则乘法AB无意义。
矩阵乘法计算如下:记r x n矩阵A与n x c矩阵B的积r x c矩阵AB为C。C的任意元素Cij等于A的第i行向量与B的第j列向量的点乘结果。
正式定义为: