kNN处理iris数据集-使用交叉验证方法确定最优 k 值

基本流程：

1、计算测试实例到所有训练集实例的距离；
2、对所有的距离进行排序，找到k个最近的邻居；
3、对k个近邻对应的结果进行合并，再排序，返回出现次数最多的那个结果。

交叉验证：

对每一个k，使用验证集计算，记录k对应的错误次数，取错误数最小的k

# -*- coding: utf-8 -*-
import os
import pandas as pd
import matplotlib.pyplot as plt
import math
import operator

#按照8:2的比例分割数据
#testSetIndex : 第几组为测试样本，取值范围0 - 4
def splitData(trainSet, testSet, testSetIndex):
    #data = pd.read_csv('iris.txt', skiprows=0, skipfooter=0, sep=r's+', encoding="utf-8", engine='python', header=None)
    data = pd.read_csv('iris.txt', encoding="utf-8", engine='python', header=None)

    for i in range(150):
        if testSetIndex == (i % 50) / 10:
            testSet.append(data.iloc[i])
        else:
            trainSet.append(data.iloc[i])
    return

#计算欧氏距离
#instance1 : 实例1
#instance2 : 实例2
#dimension ：维度
def computeDistance(instance1, instance2, dimension):
    distance = 0
    for i in xrange(dimension):
        #print(instance1[i], instance2[i])
        distance += pow((instance1[i] - instance2[i]), 2)
    return math.sqrt(distance)

#trainSet : 训练样本集
#instance : 实例数据
#k : 1 - 120
def kNN(trainSet, instance, k):
    distances = []
    dimension = len(instance) - 1
    #计算测试实例到训练集实例的距离
    for i in xrange(len(trainSet)):
        dist = computeDistance(instance, trainSet[i], dimension)
        distances.append((trainSet[i], dist))
    #对所有的距离进行排序
    distances.sort(key=operator.itemgetter(1))
    neighbors = []
    #返回k个最近邻
    for i in range(k):
        neighbors.append(distances[i][0])

    #对k个近邻进行合并，返回最多的那个
    listClass = {}
    for i in xrange(len(neighbors)):
        response = neighbors[i][4]
        if response in listClass:
            listClass[response] += 1
        else:
            listClass[response] = 1
    #排序
    sortResult = sorted(listClass.iteritems(), key = operator.itemgetter(1), reverse=True)
    return sortResult[0][0]

def main():
    trainSet = []     #训练数据集
    testSet = []      #测试数据集
    #1. 数据分割8:2
    splitData(trainSet, testSet, 4)

    #2. 使用交叉验证方法确定最优 k 值，并给出在该情形下分类器的错误分类率
    errCountSet = [0] * 120
    #9总数据切割方式，对每一个k，记录k对应的总错误次数
    for j in xrange(0, 5):
        trainSet = []
        testSet = []
        splitData(trainSet, testSet, j)
        for k in xrange(0, 120):
            #对每一个k，使用验证集计算，记录k对应的错误次数
            for i in xrange(len(testSet)):
                trainResult = kNN(trainSet, testSet[i], k + 1)
                if trainResult != testSet[i][4]:
                    errCountSet[k] = errCountSet[k] + 1

    #取错误数最小的k 有多个
    min = 1
    for i in xrange(0, 120):
        errCountSet[i] = errCountSet[i] / (30 * 5.0)
        if min > errCountSet[i]:
            min = errCountSet[i]
            #k = i + 1

    #打印错误率最小的k值
    for i in xrange(0, 120):
        if min == errCountSet[i]:
            print i + 1, min

    fig = plt.figure(figsize=(20, 15))
    ax1 = fig.add_subplot(111)
    #ax2 = fig.add_subplot(122)
    ax1.plot(range(1, 121), errCountSet)
    ax1.set_xlabel('k')
    ax1.set_ylabel('Error Rate')
    plt.show()


    return


if __name__ == "__main__":
    main()

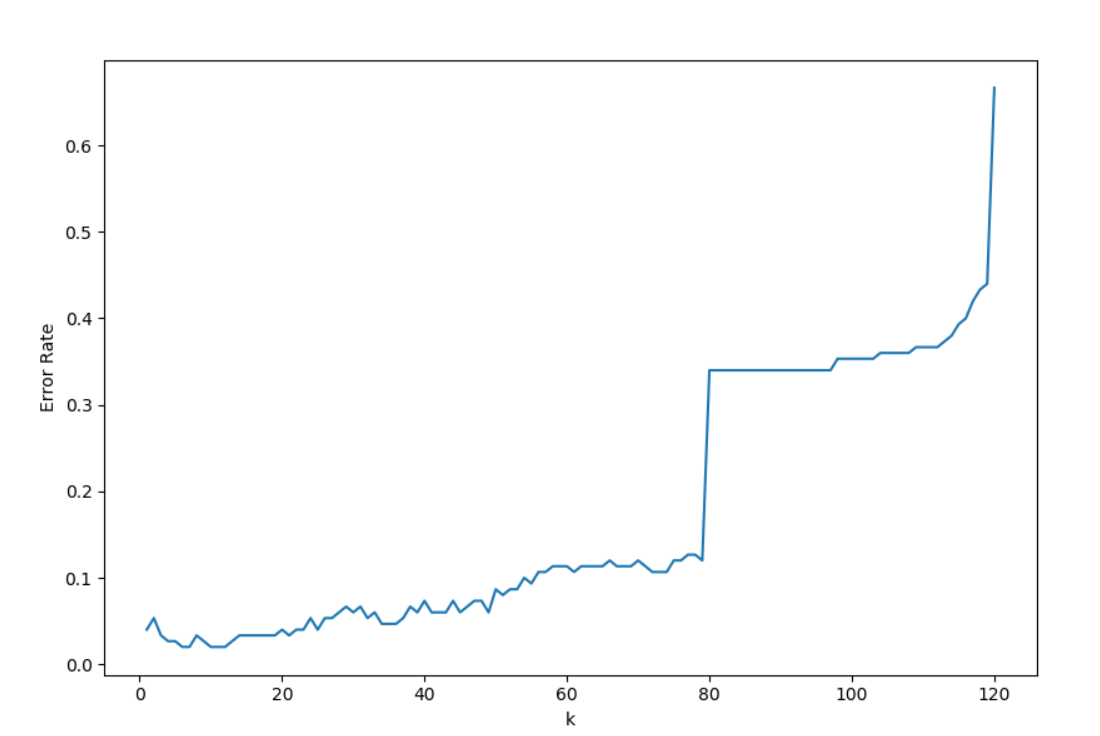
分别使用参数k=1~120进行实验，并进行交叉验证，错误分类率曲线如下：