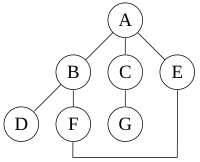
Depth-first search:
访问顺序: A, B, D, F, E, C, G.
Pseudocode
Input: A graph G and a vertex v of G
Output: A labeling of the edges in the connected component of v as discovery edges and back edges
1 procedure DFS(G,v): 2 label v as explored 3 for all edges e in G.adjacentEdges(v) do 4 if edge e is unexplored then 5 w ← G.adjacentVertex(v,e) 6 if vertex w is unexplored then 7 label e as a discovery edge 8 recursively call DFS(G,w) 9 else 10 label e as a back edge
Breadth-first search
Algorithm
The algorithm uses a queue data structure to store intermediate results as it traverses the graph, as follows:
- Enqueue the root node
- Dequeue a node and examine it
- If the element sought is found in this node, quit the search and return a result.
- Otherwise enqueue any successors (the direct child nodes) that have not yet been discovered.
- If the queue is empty, every node on the graph has been examined – quit the search and return "not found".
- If the queue is not empty, repeat from Step 2.
Note: Using a stack instead of a queue would turn this algorithm into a depth-first search.
Pseudocode
Input: A graph G and a root v of G
1 procedure BFS(G,v): 2 create a queue Q 3 enqueue v onto Q 4 mark v 5 while Q is not empty: 6 t ← Q.dequeue() 7 if t is what we are looking for: 8 return t 9 for all edges e in G.adjacentEdges(t) do 12 u ← G.adjacentVertex(t,e) 13 if u is not marked: 14 mark u 15 enqueue u onto Q 16 return none