树状数组和线段树的总结

先说树状数组吧  主要有lowbit，update，getsum

int lowbit(int x)
{
    return x&(-x);
}

int update(int x,int date)
{
    while(x<=y)
    {
        c[x]+=date;
        x+=lowbit(x);
    }
}

int getsum(int x)
{
    int ans=0;
    while(x>0)
    {
        ans+=c[x];
        x-=lowbit(x);
    }
    return ans;
}

lowbit的作用就是找到该节点的父节点或子节点   图 （https://www.cnblogs.com/George1994/p/7710886.html）

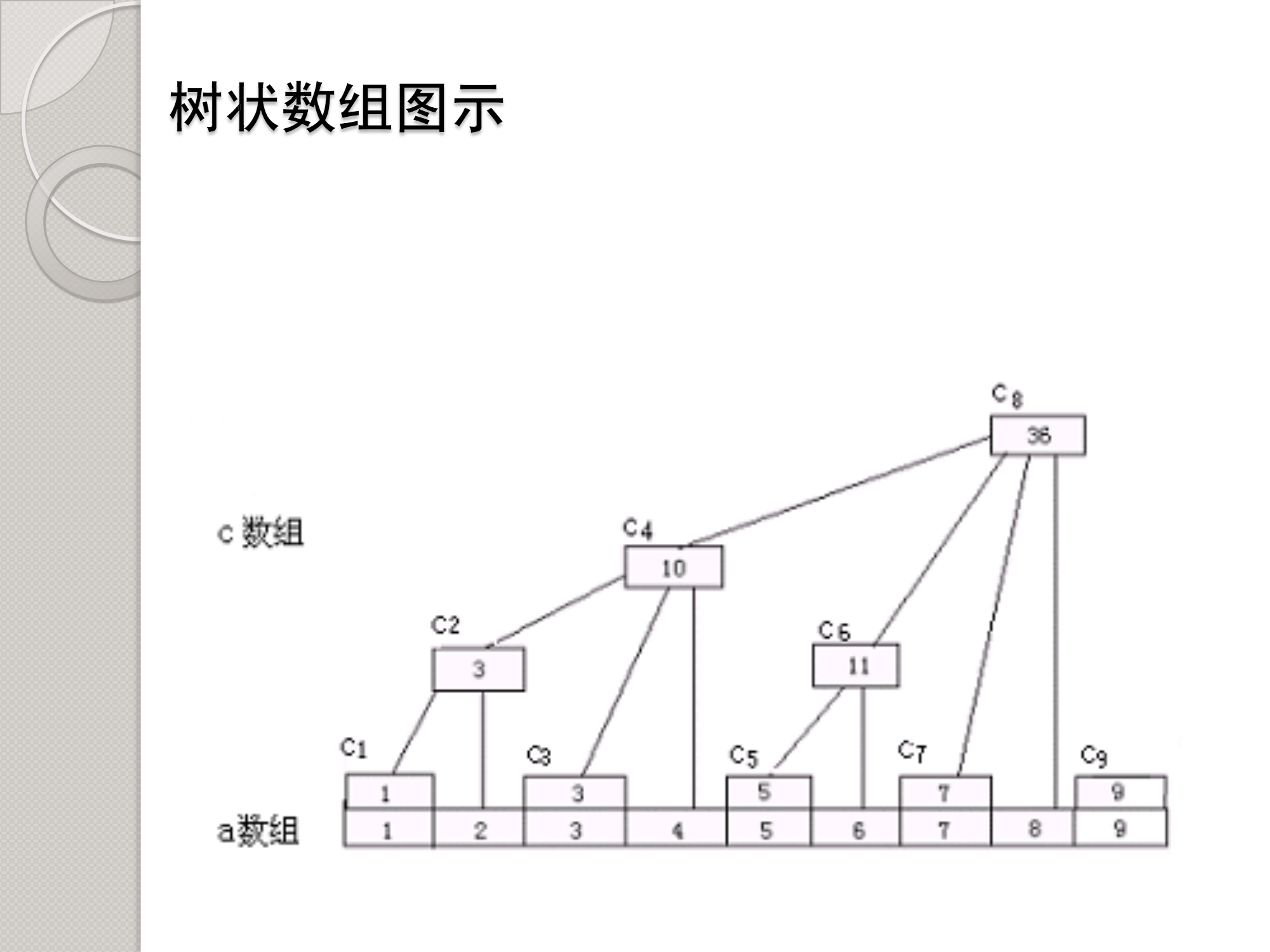
注意了  a数组存的是原来的数  c数组的意义代表着c[i] 就是前i项的和

线段树的话

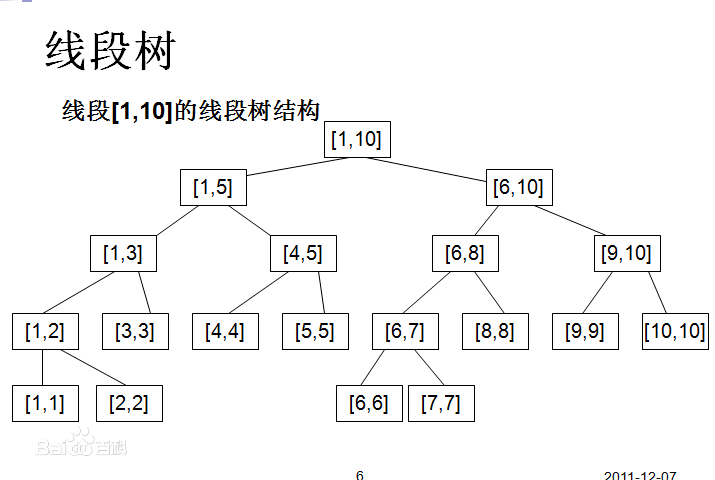
差不多两个数组搞定一个tree【n】和一个add【n】

先是建立树

线段树是从1这个节点开始的

void build(int l,int r,int k)//l，r为建树的范围 
{
    if(l==r)
    {
        cin>>tree[k];
        return ;
    }
    int m=(l+r)>>1;
    build(l,m,k<<1);//递归建立数 
    build(m+1,r,k<<1|1);
    tree[k]=tree[k<<1]+tree[k<<1|1];//求和 
}

自我觉得这个是比较灵活的，对这个改动一下就成为不同的功能，比如最大值

void build(int l,int r,int k)
{
    if(l==r)
    {
        cin>>tree[k];
        return ;
    }
    int m=(l+r)>>1;
    build(l,m,k<<1);
    build(m+1,r,k<<1|1);
    //tree[k]=tree[k<<1]+tree[k<<1|1];
    tree[k]=max(tree[k<<1],tree[k<<1|1]); 
}

这样就变成了父节点 为子节点的最大值

然后是点更新

void update(int ee,int c,int l,int r,int k)
{
    if(l==r)
    {
        tree[k]+=c;
        //tree[k]=c;  这样就是更改这个数，而不是加 
        return ;
    }
    int m=(l+r)>>1;
    if(ee<=m) update(ee,c,l,m,k<<1);//ee为需要更新的叶子节点，通过递归找 
    else update(ee,c,m+1,r,k<<1|1);
    tree[k]=tree[k<<1]+tree[k<<1|1];
}

然后是区间更新  ，这里需要懒标记，这个确实比较难理解

void update(int x,int y,int c,int l,int r,int k)//x，y为需要更新区间，l，r为k这一节点的管理范围 
{
    if(x<=l&&y>=r)
    {
        tree[k]=c*(r-l+1);//这一点为c乘以这一点管理的数量
        add[k]=c;//把这一点标记一下，为懒标记
        return;//注意是结束了 
    }
    int m=(l+r)>>1;
    pushdown(k,m-l+1,r-m);//下推标记
    if(x<=m) update(x,y,c,l,m,k<<1);
    if(y>m) update(x,y,c,m+1,r,k<<1|1);//注意 这里不是else 而是都要更新并查找 
    tree[k]=tree[k<<1]+tree[k<<1|1]; 
} 

void pushdown(int k,int ln,int rn)//ln,rn为左子树，右子树的数字数量。 
{
    if(add[k])
    {
        add[k<<1]+=add[k];
        add[k<<1|1]+=add[k];//传递这个标记
        
        sum[k<<1]+=add[k]*ln;
        sum[k<<1|1]+=add[k]*rn;
        add[k]=0;
    }
} 

上面是要求和的下推标记，但如果说是这道题

POJ - 2299 

为这个区间都改变成一样的数，而不是相加一样的数

void pushdown(int k,int ln,int rn){
    if(add[k]){
        add[k<<1]=add[k];
        add[k<<1|1]=add[k];

        sum[k<<1]=add[k]*ln;
        sum[k<<1|1]=add[k]*rn;
        add[k]=0;
    }
}

最后是区间求和

int query(int x,int y,int l,int r,int k)
{
    if(x<=l&&r<=y)
    {
        return tree[k];
    }
    int m=(l+r)>>1;
    pushdown(k,m+1-l,r-m);
    
    int ans=0;
    if(x<=m) ans+=query(x,y,l,m,k<<1);
    if(y>m) ans+=query(x,y,m+1,r,k<<1|1);
    return ans;
}