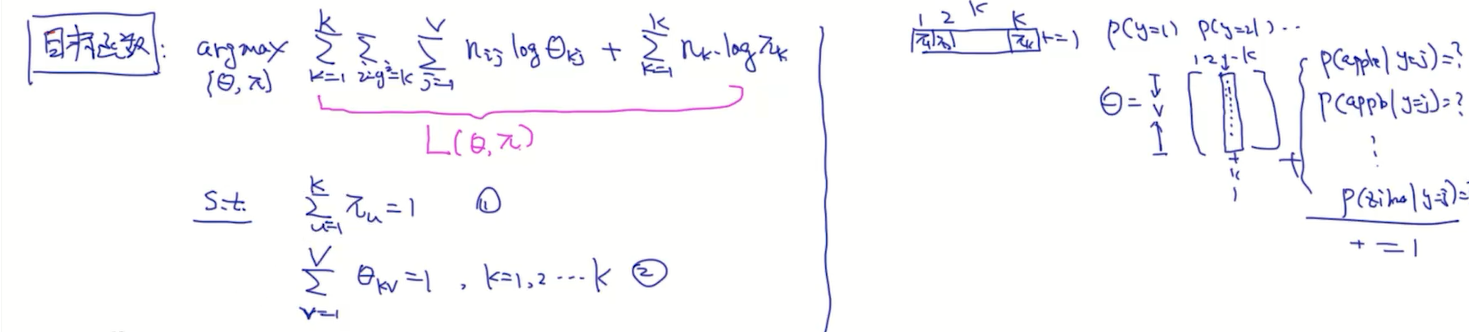1.词性
2.马尔科夫模型与维特比
3.蒙特卡罗
4.构建目标函数
词性标准
In corpus linguistics, part-of-speech tagging (POS tagging or also called grammatical tagging or word-category disambiguation,
is the process of marking up the words in a text (corpus) as corresponding to a particular part of speech, based on both its definition, as well as its context —ie.
relationship with adjacent and related words in a phrase, sentence, or paragraph.
A simplified form of this is commonly taught to school-age children, in the identification of words as nouns, verbs, adjectives, adverbs, etc.

隐含马尔可夫模型(Hidden Markov Model)
隐含马尔可夫模型并不是俄罗斯数学家马尔可夫发明的,而是美国数学家鲍姆提出的,隐含马尔可夫模型的训练方法(鲍姆-韦尔奇算法)也是以他名字命名的。隐含马尔可夫模型一直被认为是解决大多数自然语言处理问题最为快速、有效的方法。
马尔可夫假设
随机过程中各个状态St的概率分布,只与它的前一个状态St-1有关,即P(St|S1,S2,S3,…,St-1) = P(St|St-1)。
比如,对于天气预报,硬性假定今天的气温只与昨天有关而和前天无关。当然这种假设未必适合所有的应用,但是至少对以前很多不好解决的问题给出了近似解。
马尔可夫链
符合马尔可夫假设的随机过程称为马尔可夫过程,也称为马尔可夫链。
在这个马尔可夫链中,四个圈表示四个状态,每条边表示一个可能的状态转换,边上的权值是转移概率。
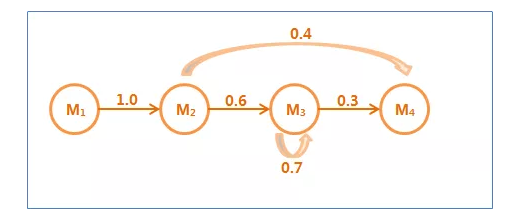
隐含马尔可夫链是上述马尔可夫链的一个扩展:任一时刻t的状态St是不可见的。所以观察者没法通过观察到一个状态序列S1,S2,S3,…,ST来推测转移概率等参数。
但是隐含马尔可夫模型在每个时刻t会输出一个符号Ot,而且Ot和St相关且仅和St相关。这称为独立输出假设。
隐含马尔可夫模型的结构如下图,其中隐含的状态S1,S2,S3,…是一个典型的马尔可夫链。鲍姆把这种模型称为“隐含”马尔可夫模型。
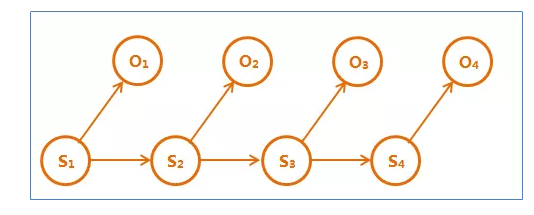
隐含马尔可夫模型的三个基本问题
1、给定一个模型,如何计算某个特定的输出序列的概率?
Forward-Backward算法
2、给定一个模型和某个特定的输出序列,如何找到最可能产生这个输出的状态序列?
维特比算法
3、给定足够量的观测数据,如何估计隐含马尔可夫模型的参数?
训练隐含马尔可夫模型更实用的方式是仅仅通过大量观测到的信号O1,O2,O3,….就能推算模型参数的P(St|St-1)和P(Ot|St)的方法(无监督训练算法),其中主要使用鲍姆-韦尔奇算法。
隐含马尔可夫模型的五元组
HMM是一个五元组(O , Q , O0,A , B):
1、O:{o1,o2,…,ot}是状态集合,也称为观测序列。
2、Q:{q1,q2,…,qv}是一组输出结果,也称为隐序列。
3、Aij = P(qj|qi):转移概率分布
4、Bij = P(oj|qi):发射概率分布
5、O0是初始状态,有些还有终止状态。
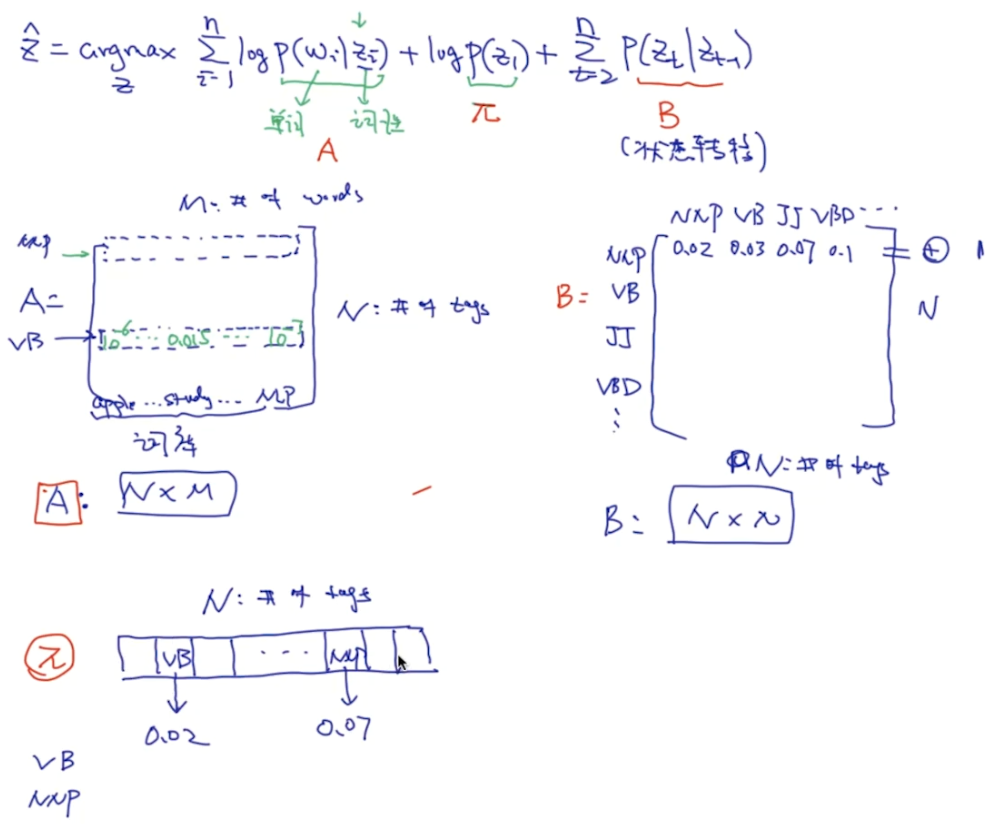
构建词性与词频--词袋:

tag2id, id2tag = {}, {} # maps tag to id . tag2id: {"VB": 0, "NNP":1,..} , id2tag: {0: "VB", 1: "NNP"....}
word2id, id2word = {}, {} # maps word to id
for line in open('traindata.txt'):
items = line.split('/')
word, tag = items[0], items[1].rstrip() # 抽取每一行里的单词和词性
if word not in word2id:
word2id[word] = len(word2id)
id2word[len(id2word)] = word
if tag not in tag2id:
tag2id[tag] = len(tag2id)
id2tag[len(id2tag)] = tag
M = len(word2id) # M: 词典的大小、# of words in dictionary
N = len(tag2id) # N: 词性的种类个数 # of tags in tag set
print((M,N))


# 构建 pi, A, B import numpy as np pi = np.zeros(N) # 每个词性出现在句子中第一个位置的概率, N: # of tags pi[i]: tag i出现在句子中第一个位置的概率 A = np.zeros((N, M)) # A[i][j]: 给定tag i, 出现单词j的概率。 N: # of tags M: # of words in dictionary B = np.zeros((N,N)) # B[i][j]: 之前的状态是i, 之后转换成转态j的概率 N: # of tags
读入数据

prev_tag = "" for line in open('traindata.txt'): items = line.split('/') wordId, tagId = word2id[items[0]], tag2id[items[1].rstrip()] if prev_tag == "": # 这意味着是句子的开始 pi[tagId] += 1 A[tagId][wordId] += 1 else: # 如果不是句子的开头 A[tagId][wordId] += 1 B[tag2id[prev_tag]][tagId] += 1 if items[0] == ".": prev_tag = "" else: prev_tag = items[1].rstrip() print(A.shape) print(B.shape) print(pi.shape)
标准化(概率化)

# normalize pi = pi/sum(pi) for i in range(N): A[i] /= sum(A[i]) B[i] /= sum(B[i]) # 到此为止计算完了模型的所有的参数: pi, A, B

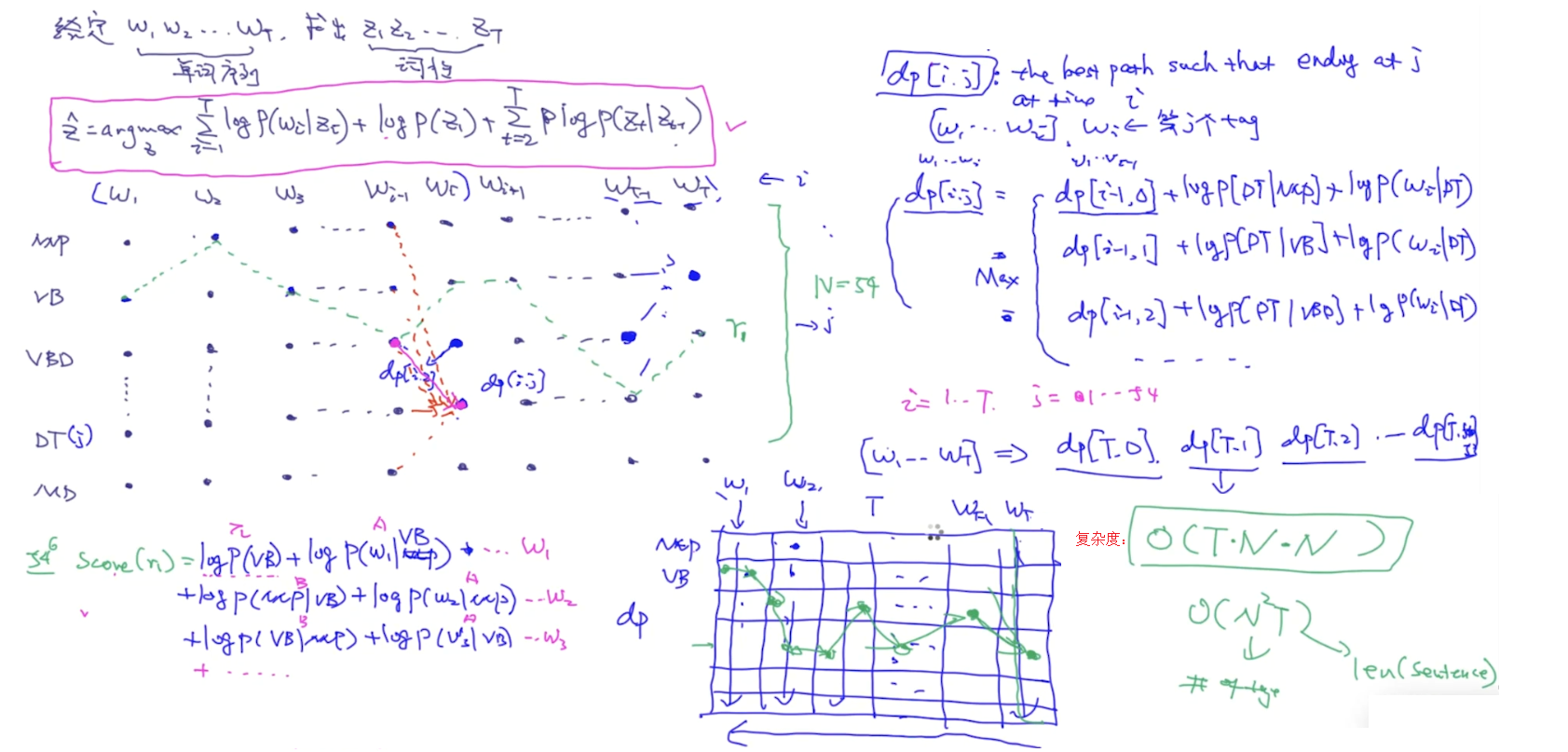

def log(v): if v == 0: return np.log(v+0.000001) return np.log(v) def viterbi(x, pi, A, B): """ x: user input string/sentence: x: "I like playing soccer" pi: initial probability of tags A: 给定tag, 每个单词出现的概率 B: tag之间的转移概率 """ x = [word2id[word] for word in x.split(" ")] # x: [4521, 412, 542 ..] T = len(x) dp = np.zeros((T,N)) # dp[i][j]: w1...wi, 假设wi的tag是第j个tag ptr = np.array([[0 for x in range(N)] for y in range(T)] ) # T*N # TODO: ptr = np.zeros((T,N), dtype=int) for j in range(N): # basecase for DP算法 dp[0][j] = log(pi[j]) + log(A[j][x[0]]) for i in range(1,T): # 每个单词 for j in range(N): # 每个词性 # TODO: 以下几行代码可以写成一行(vectorize的操作, 会使得效率变高) dp[i][j] = -9999999 for k in range(N): # 从每一个k可以到达j score = dp[i-1][k] + log(B[k][j]) + log(A[j][x[i]]) if score > dp[i][j]: dp[i][j] = score ptr[i][j] = k # decoding: 把最好的tag sequence 打印出来 best_seq = [0]*T # best_seq = [1,5,2,23,4,...] # step1: 找出对应于最后一个单词的词性 best_seq[T-1] = np.argmax(dp[T-1]) # step2: 通过从后到前的循环来依次求出每个单词的词性 for i in range(T-2, -1, -1): # T-2, T-1,... 1, 0 best_seq[i] = ptr[i+1][best_seq[i+1]] # 到目前为止, best_seq存放了对应于x的 词性序列 for i in range(len(best_seq)): print (id2tag[best_seq[i]])
结果:
x = "Social Security number , passport number and details about the services provided for the payment" viterbi(x, pi, A, B)

拓展:

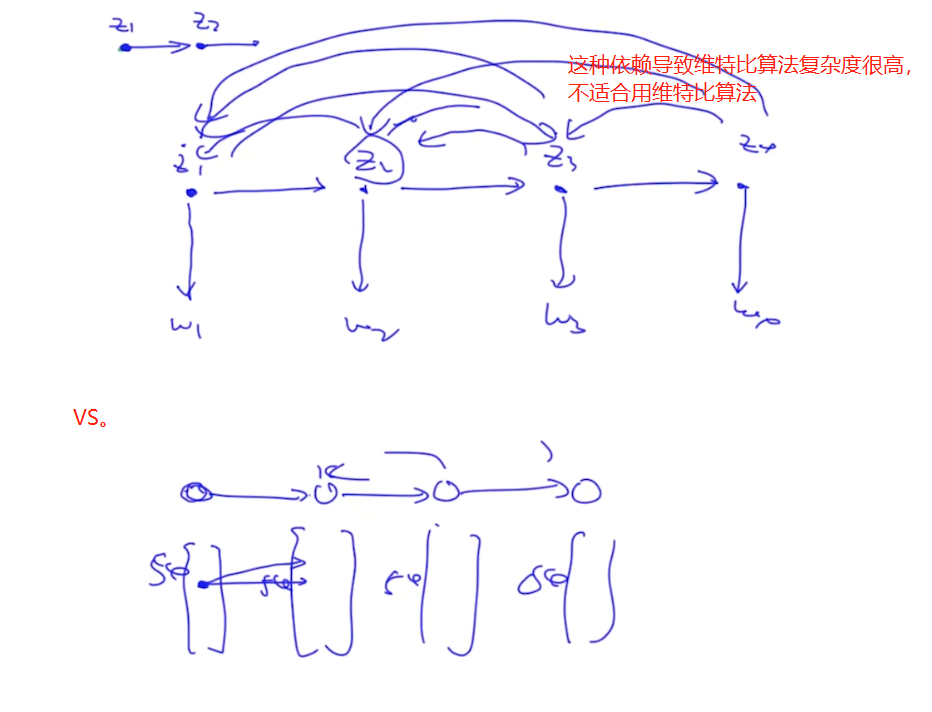
蒙特卡罗

构建目标函数

实验次数太少会导致不准确,只有观测的数据越来愈多的时候才会更准确。
MLE与MAP之间的关系
最大似然估计(MLE)和最大后验概率(MAP)都是用于估计概率分布。它们之所以相似,因为它们得到的都是一个单一逼近,而不是一个完整的概率分布。
在机器学习里面,MLE很常见,有时候我们甚至在不知情的情况下用到它。
例如,当我们用数据集拟合高斯分布时,把数据集样本均值和样本方差,用作高斯分布的参数,这就是MLE。 因为如果我们对高斯函数的均值和方差求偏导数,并优化使其最大(即求导数为零的点),那么我们得到的是计算样本均值和样本方差的函数。
另一个例子,机器学习和深度学习(神经网络等)中的大多数分类问题,都可以解释为MLE——softmax cross entropy loss。
Maximum Likelihood Estimation or MLE
我们先看看MLE,现在我们有一个关于θ的似然函数:
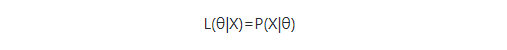
那么MLE就是:
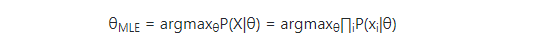
在这里,P(xi|θ)≤1,相乘的结果由于取数值小于1的乘积会随着这些项数量的增加而逼近0,特别在计算机上,很容易产生计算下溢。因此,我们对原有函数做一下变换,取对数log,使其每一项相乘变换为每一项相加。因为对数函数仍然是单调增加,所以最大化原有的函数与最大化取对数之后的函数是等价的。变换后,我们得到如下函数:
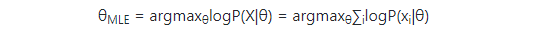
通过梯度下降(上升)方法对θ优化,求出上述函数最大值,这就是最大似然逼近(MLE)。
Maximum A Posteriori Estimation or MAP
我们再来看MAP,根据贝叶斯公式,后验概率定义如下:
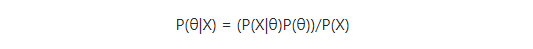
我们可以把分母拿掉,因为P(X)不受θ影响,得到:
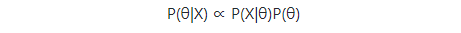
因此
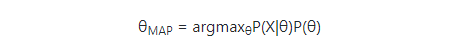
同样,取对数,得到

对比MLE,MAP只是多了一项P(θ),就是说,最大化似然函数加权先验θ概率,就是MAP。
MLE is a special case of MAP
来看一个特殊例子,假如P(θ)是一个均匀分布,MAP函数如下:
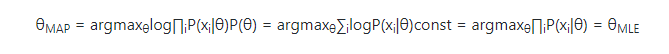
可见,MLE是MAP的一个特例。
同时当样本越来愈大的时候MAP 会趋近于 MLE


朴素贝叶斯: