红黑树red-black tree

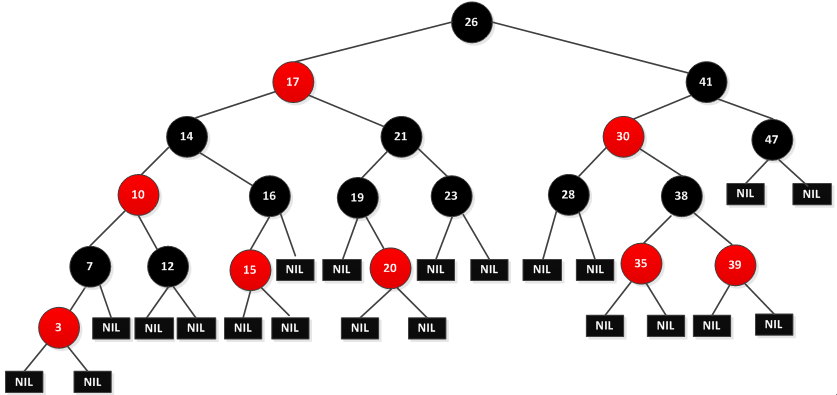
书籍：《算法导论》第13章

红黑树性质：
1. 每个节点要么red要么black。
2. 根节点是black节点。
3. 叶子节点是black节点。
4. red节点的左右儿子节点都是black节点。
5. 从同一节点出发，到达可达的叶子节点路径上，黑色节点个数都一样。

节点数据结构：

class RBNode {

    RBNode left , right ,parent;

    int color;

}

红黑树是相对平衡的树证明：
红黑树可以保证：

h <= 2*lg(n+1) ，n表示红黑树的内部节点数，除了叶子节点和根节点都是内部节点。h表示树的高度。
证明：
定义：bh(x):black height，黑高度，指从节点x到叶子节点的路径上黑节点个数。
1. 使用归纳证明，以x为根的红黑树，内部节点个数n至少为2^bh(x) -1 个。

下面通过"数学归纳法"开始论证高度为h的红黑树，它的包含的内节点个数至少为 2^bh(x)-1个"。 

(01) 当树的高度h=0时，
内节点个数是0，bh(x) 为0，2^bh(x)-1 也为 0。显然，原命题成立。

(02) 当h>0，且树的高度为 h-1 时，它包含的节点个数至少为 2^{bh(x)-1}-1。这个是根据(01)推断出来的！

下面，由树的高度为 h-1 的已知条件推出“树的高度为 h 时，它所包含的节点树为 2^bh(x)-1”。

当树的高度为 h 时，
对于节点x(x为根节点)，其黑高度为bh(x)。
对于节点x的左右子树，它们黑高度为 bh(x) 或者 bh(x)-1。
根据(02)的已知条件，我们已知 "x的左右子树，即高度为 h-1 的节点，它包含的节点至少为 2^{bh(x)-1}-1 个"；

所以，节点x所包含的节点至少为 ( 2^{bh(x)-1}-1 ) + ( 2^{bh(x)-1}-1 ) + 1 = 2^{bh(x)-1}。即节点x所包含的节点至少为 2^{bh(x)-1} 。
因此，原命题成立。

由(01)、(02)得出，"高度为h的红黑树，它的包含的内节点个数至少为 2^bh(x)-1个"。
因此，“一棵含有n个节点的红黑树的高度至多为2log(n+1)”。

2. 假设红黑树的高度为h，由性质4可知红黑树的黑高度bh(root)>=h/2，因此，可得
n >= 2^(h/2)-1
化简得：
h <= 2*lg(n+1) 得证。