P2668 斗地主
题目描述
牛牛最近迷上了一种叫斗地主的扑克游戏。斗地主是一种使用黑桃、红心、梅花、方片的A到K加上大小王的共54张牌来进行的扑克牌游戏。在斗地主中,牌的大小关系根据牌的数码表示如下:3<4<5<6<7<8<9<10<J<Q<K<A<2<小王<大王,而花色并不对牌的大小产生影响。每一局游戏中,一副手牌由n张牌组成。游戏者每次可以根据规定的牌型进行出牌,首先打光自己的手牌一方取得游戏的胜利。
现在,牛牛只想知道,对于自己的若干组手牌,分别最少需要多少次出牌可以将它们打光。请你帮他解决这个问题。
需要注意的是,本题中游戏者每次可以出手的牌型与一般的斗地主相似而略有不同。
具体规则如下:
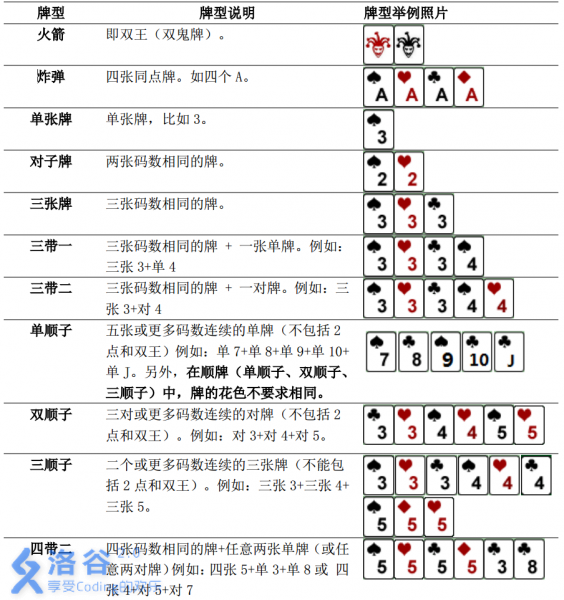
输入输出格式
输入格式:
第一行包含用空格隔开的2个正整数T和n,表示手牌的组数以及每组手牌的张数。
接下来T组数据,每组数据n行,每行一个非负整数对aibi表示一张牌,其中ai示牌的数码,bi表示牌的花色,中间用空格隔开。特别的,我们用1来表示数码A,11表示数码J,12表示数码Q,13表示数码K;黑桃、红心、梅花、方片分别用1-4来表示;小王的表示方法为01,大王的表示方法为02。
输出格式:
共T行,每行一个整数,表示打光第i手牌的最少次数。
输入输出样例
1 8 7 4 8 4 9 1 10 4 11 1 5 1 1 4 1 1
3
1 17 12 3 4 3 2 3 5 4 10 2 3 3 12 2 0 1 1 3 10 1 6 2 12 1 11 3 5 2 12 4 2 2 7 2
6
说明
样例1说明
共有1组手牌,包含8张牌:方片7,方片8,黑桃9,方片10,黑桃J,黑桃5,方片A以及黑桃A。可以通过打单顺子(方片7,方片8,黑桃9,方片10,黑桃J),单张牌(黑桃5)以及对子牌(黑桃A以及方片A)在3次内打光。
对于不同的测试点, 我们约定手牌组数T与张数n的规模如下:
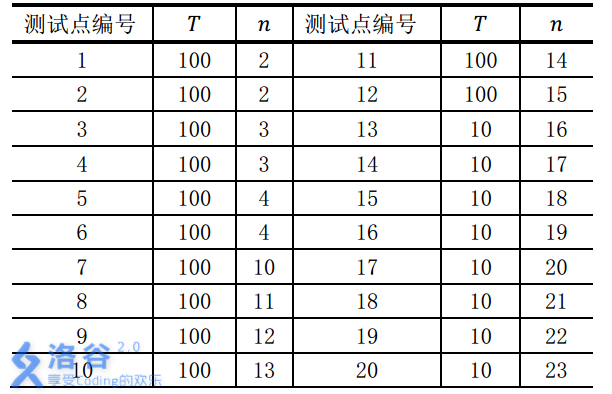
数据保证:所有的手牌都是随机生成的。
思路:
加点小技巧,用dp实现找最小,而不用贪心,解决拆开出牌更优的问题
dfs+dp水过
上代码:
#include<iostream> #include<cstdio> #include<cstring> #include<cmath> using namespace std; const int MAXN=24; int T,n,p,hs,ans; int dp[MAXN][MAXN][MAXN][MAXN],card_num[MAXN],happen[MAXN/4]; int take_num[5]= {0,5,3,2}; int read(int & n) { char c='-'; int x=0; while(c<'0'||c>'9')c=getchar(); while(c>='0'&&c<='9') { x=x*10+(c-48); c=getchar(); } n=x; } int calc(int one,int two,int three,int four,int king) { if(king==1) { // 只有一张大小王 one++;// 看做单牌处理 king=0; } if(king==0) return dp[four][three][two][one]; else return min(dp[four][three][two][one+2],dp[four][three][two][one]+1); } void dfs(int now) { //now是指已经操作的次数 if(now>ans) return ; memset(happen,0,sizeof(happen));// 初始化 for(int i=2; i<=14; i++) happen[card_num[i]]++; ans=min(ans,now+calc(happen[1],happen[2],happen[3],happen[4],card_num[0])); for(int k=1; k<=3; k++) { // 顺子 for(int i=3; i<=14; i++) { int j; for(j=i; j<=14&&card_num[j]>=k; j++) { card_num[j]-=k; if(j-i+1>=take_num[k]) dfs(now+1); } for(j--; j>=i; j--) card_num[j]+=k; } } } int main() { read(T); read(n); memset(dp,1,sizeof dp); dp[0][0][0][0]=0; // dp[i][j][k][l]表示打出i套四张,j套三张,k套两站,l张单牌所需要的最少步数 for(int i=0; i<=n; i++) //四张 for(int j=0; j<=n; j++) //三张 for(int k=0; k<=n; k++) //两张 for(int l=0; l<=n; l++) //一张 if(i*4+j*3+k*2+l*1<=n) { dp[i][j][k][l]=i+j+k+l;//最坏的情况 if(i) { if(k>=2) dp[i][j][k][l]=min(dp[i][j][k][l],dp[i-1][j][k-2][l]+1); // 四带一对对牌 if(l>=2) dp[i][j][k][l]=min(dp[i][j][k][l],dp[i-1][j][k][l-2]+1); // 一对单牌 dp[i][j][k][l]=min(dp[i][j][k][l],dp[i-1][j][k][l]+1); //啥都不带 } if(j) { if(k) dp[i][j][k][l]=min(dp[i][j][k][l],dp[i][j-1][k-1][l]+1); // 3带对 if(l) dp[i][j][k][l]=min(dp[i][j][k][l],dp[i][j-1][k][l-1]+1); // 3带单 dp[i][j][k][l]=min(dp[i][j][k][l],dp[i][j-1][k][l]+1); // 什么都不带 } if(k) dp[i][j][k][l]=min(dp[i][j][k][l],dp[i][j][k-1][l]+1); if(l) dp[i][j][k][l]=min(dp[i][j][k][l],dp[i][j][k][l-1]+1); } while(T--) { memset(card_num,0,sizeof(card_num));// 初始化 ans=n; for(int i=1; i<=n; i++) { read(p); read(hs); if(p==0) card_num[0]++;//大小王 else if(p==1) card_num[14]++;// A else card_num[p]++; } dfs(0); printf("%d ",ans); } return 0; }
P1197 [JSOI2008]星球大战
题目描述
很久以前,在一个遥远的星系,一个黑暗的帝国靠着它的超级武器统治者整个星系。某一天,凭着一个偶然的机遇,一支反抗军摧毁了帝国的超级武器,并攻下了星系中几乎所有的星球。这些星球通过特殊的以太隧道互相直接或间接地连接。
但好景不长,很快帝国又重新造出了他的超级武器。凭借这超级武器的力量,帝国开始有计划地摧毁反抗军占领的星球。由于星球的不断被摧毁,两个星球之间的通讯通道也开始不可靠起来。现在,反抗军首领交给你一个任务:给出原来两个星球之间的以太隧道连通情况以及帝国打击的星球顺序,以尽量快的速度求出每一次打击之后反抗军占据的星球的连通快的个数。(如果两个星球可以通过现存的以太通道直接或间接地连通,则这两个星球在同一个连通块中)。
输入输出格式
输入格式:
输入文件第一行包含两个整数,N (1 <= N <= 2M) 和M (1 <= M <= 200,000),分别表示星球的数目和以太隧道的数目。星球用0~N-1的整数编号。
接下来的M行,每行包括两个整数X, Y,其中(0<=X<>Y<N),表示星球X和星球Y之间有以太隧道。注意所有的以太隧道都是双向的。
接下来一行是一个整数K,表示帝国计划打击的星球个数。
接下来的K行每行一个整数X,满足0<=X<N,表示帝国计划打击的星球编号。帝国总是按输入的顺序依次摧毁星球的。
输出格式:
输出文件的第一行是开始时星球的连通块个数。
接下来的K行,每行一个整数,表示经过该次打击后现存星球的连通块个数。
输入输出样例
8 13 0 1 1 6 6 5 5 0 0 6 1 2 2 3 3 4 4 5 7 1 7 2 7 6 3 6 5 1 6 3 5 7
1 1 1 2 3 3
说明
[JSOI2008]
思路:
求最强连通分量,因为打击某个点比较难实现,所以我们可以试着倒叙添点,然后依次求连通分量
上代码:
#include<iostream> #include<cstdio> using namespace std; const int maxx = 400003; int n,m,u,v,head[maxx],num_edge,k; int dad[maxx],hit[maxx],vis[maxx],ans[maxx]; struct Edge{ int pre,to; }edge[maxx]; void build_edge(int u,int v) { edge[++num_edge].pre = head[u]; edge[num_edge].to = v; head[u] = num_edge; } int find(int x) { if(dad[x] != x) dad[x] = find(dad[x]); return dad[x]; } void unionn(int a,int b) { int t1 = find(a),t2 = find(b); if(t1!=t2) dad[t1] = t2; } int main() { scanf("%d%d",&n,&m); for(int i=0; i<n; i++) dad[i] = i; for(int i=0; i<m; i++) { scanf("%d%d",&u,&v); build_edge(u,v); build_edge(v,u); } scanf("%d",&k); for(int i=0; i<k; i++) { scanf("%d",&hit[i]); vis[hit[i]] = 1; } for(int i=0; i<n; i++) { if(!vis[i]) { for(int j=head[i]; j; j=edge[j].pre) { int q = edge[j].to; if(!vis[q]) unionn(i,q); } } } for(int i=0; i<n; i++) if(!vis[i] && find(i) == i) ans[k]++; for(int i=k-1; i>=0; i--) { int tot = 0; vis[hit[i]] = 0; for(int j=head[hit[i]]; j; j=edge[j].pre) { int p = edge[j].to; if(!vis[p]) { int a = find(hit[i]),b = find(p); if(a != b) { dad[a] = b; tot++; } } } ans[i] = ans[i+1]-tot+1; } for(int i=0; i<=k; i++) printf("%d ",ans[i]); return 0; }
P1514 引水入城
题目描述
在一个遥远的国度,一侧是风景秀美的湖泊,另一侧则是漫无边际的沙漠。该国的行政区划十分特殊,刚好构成一个N 行M 列的矩形,如上图所示,其中每个格子都代表一座城市,每座城市都有一个海拔高度。
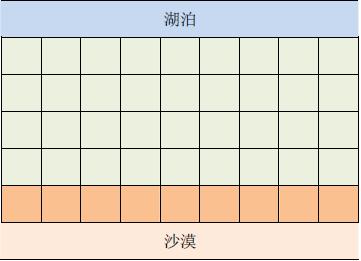
为了使居民们都尽可能饮用到清澈的湖水,现在要在某些城市建造水利设施。水利设施有两种,分别为蓄水厂和输水站。蓄水厂的功能是利用水泵将湖泊中的水抽取到所在城市的蓄水池中。
因此,只有与湖泊毗邻的第1 行的城市可以建造蓄水厂。而输水站的功能则是通过输水管线利用高度落差,将湖水从高处向低处输送。故一座城市能建造输水站的前提,是存在比它海拔更高且拥有公共边的相邻城市,已经建有水利设施。由于第N 行的城市靠近沙漠,是该国的干旱区,所以要求其中的每座城市都建有水利设施。那么,这个要求能否满足呢?如果能,请计算最少建造几个蓄水厂;如果不能,求干旱区中不可能建有水利设施的城市数目。
输入输出格式
输入格式:
输入文件的每行中两个数之间用一个空格隔开。输入的第一行是两个正整数N 和M,表示矩形的规模。接下来N 行,每行M 个正整数,依次代表每座城市的海拔高度。
输出格式:
输出有两行。如果能满足要求,输出的第一行是整数1,第二行是一个整数,代表最少建造几个蓄水厂;如果不能满足要求,输出的第一行是整数0,第二行是一个整数,代表有几座干旱区中的城市不可能建有水利设施。
输入输出样例
【输入样例1】 2 5 9 1 5 4 3 8 7 6 1 2 【输入样例2】 3 6 8 4 5 6 4 4 7 3 4 3 3 3 3 2 2 1 1 2
【输出样例1】 1 1 【输出样例2】 1 3
说明
【样例1 说明】
只需要在海拔为9 的那座城市中建造蓄水厂,即可满足要求。
【样例2 说明】
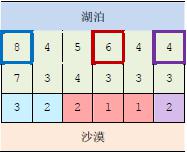
上图中,在3 个粗线框出的城市中建造蓄水厂,可以满足要求。以这3 个蓄水厂为源头
在干旱区中建造的输水站分别用3 种颜色标出。当然,建造方法可能不唯一。
【数据范围】
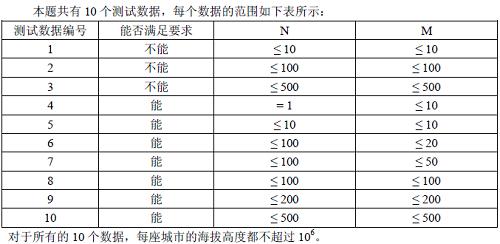
思路:
看数据范围,我们就知道此题是道骗分题。。。
30分做法:前三个点,不能满足要求,so we make a easy dfs 水过
40分做法:前三个点水过,第4个点枚举。。。
80分做法:漂亮的dfs(研究题目发现一个蓄水厂会给某个区间送水,so线段覆盖),then we found 有两个点TLE,偷窥数据发现这两个点是不能满足条件的情况
AC做法:80分做法+30分做法。。。。当然这是在看了数据的情况下的做法,so 想要一步AC的思思思~~~
上代码:
#include<iostream> #include<cstdio> #include<algorithm> using namespace std; const int maxx = 501; int n,m,map[maxx][maxx],ans; bool vis[maxx][maxx],visit[maxx]; int dx[4]={1,-1,0,0}, dy[4]={0,0,1,-1}; struct Node{ int l,r; Node() { //初始化 l = 10000; r = -1; } }node[maxx]; int Min(int a,int b) { return a < b ? a:b; } int Max(int a,int b) { return a > b ? a:b; } bool bianjie(int x,int y) { if(x>0 && x<=n && y>0 && y<=m) return true; return false; } int no_dfs(int x,int y) { //30分搜索 if(x == n) ans++; vis[x][y] = true; for(int i=0; i<4; i++) { int xx=x+dx[i], yy=y+dy[i]; if(map[xx][yy] < map[x][y] && !vis[xx][yy] && bianjie(xx,yy)) { no_dfs(xx,yy); } } } int normal_dfs(int x,int y,int ID) { //80分搜索 if(x == n) { node[ID].l = Min(node[ID].l,y); node[ID].r = Max(node[ID].r,y); if(!visit[y]) visit[y] = true; } for(int i=0; i<4; i++) { int xx=x+dx[i], yy=y+dy[i]; if(map[xx][yy] < map[x][y] && bianjie(xx,yy)) { normal_dfs(xx,yy,ID); } } } bool cmp(Node a,Node b) { if(a.l != b.l) return a.l < b.l; else return a.r > b.r; } int main() { scanf("%d%d",&n,&m); for(int i=1; i<=n; i++) for(int j=1; j<=m; j++) scanf("%d",&map[i][j]); for(int i=1; i<=m; i++) if(!vis[1][i]) no_dfs(1,i); if(ans != m) { printf("0 %d",m-ans); return 0; } for(int i=1; i<=m; i++) normal_dfs(1,i,i); sort(node+1,node+m+1,cmp); int q = 0,tot = 0,zz = 0; for(int i=1; i<=m; i++) { if(node[i].l > m) continue; if(node[i].l <= q+1) zz = Max(zz, node[i].r); else { q = zz; tot++; zz = Max(zz, node[i].r); } } if(q != m) tot++; printf("1 %d",tot); return 0; }
P1314 聪明的质监员
题目描述
小T 是一名质量监督员,最近负责检验一批矿产的质量。这批矿产共有 n 个矿石,从 1到n 逐一编号,每个矿石都有自己的重量 wi 以及价值vi 。检验矿产的流程是:
1 、给定m 个区间[Li,Ri];
2 、选出一个参数 W;
3 、对于一个区间[Li,Ri],计算矿石在这个区间上的检验值Yi:
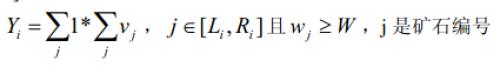
这批矿产的检验结果Y 为各个区间的检验值之和。即:Y1+Y2...+Ym
若这批矿产的检验结果与所给标准值S 相差太多,就需要再去检验另一批矿产。小T
不想费时间去检验另一批矿产,所以他想通过调整参数W 的值,让检验结果尽可能的靠近
标准值S,即使得S-Y 的绝对值最小。请你帮忙求出这个最小值。
输入输出格式
输入格式:
输入文件qc.in 。
第一行包含三个整数n,m,S,分别表示矿石的个数、区间的个数和标准值。
接下来的n 行,每行2个整数,中间用空格隔开,第i+1 行表示 i 号矿石的重量 wi 和价值vi。
接下来的m 行,表示区间,每行2 个整数,中间用空格隔开,第i+n+1 行表示区间[Li,Ri]的两个端点Li 和Ri。注意:不同区间可能重合或相互重叠。
输出格式:
输出文件名为qc.out。
输出只有一行,包含一个整数,表示所求的最小值。
输入输出样例
5 3 15 1 5 2 5 3 5 4 5 5 5 1 5 2 4 3 3
10
说明
【输入输出样例说明】
当W 选4 的时候,三个区间上检验值分别为 20、5 、0 ,这批矿产的检验结果为 25,此
时与标准值S 相差最小为10。
【数据范围】
对于10% 的数据,有 1 ≤n ,m≤10;
对于30% 的数据,有 1 ≤n ,m≤500 ;
对于50% 的数据,有 1 ≤n ,m≤5,000;
对于70% 的数据,有 1 ≤n ,m≤10,000 ;
对于100%的数据,有 1 ≤n ,m≤200,000,0 < wi, vi≤10^6,0 < S≤10^12,1 ≤Li ≤Ri ≤n 。
思路:
二分答案+前缀和 (二分W)
注意读懂题目啊。。。。这个题可能是语文老师出的吧![]()
为什么用前缀和??因为有区间啊,一般有区间的还要求和的都用前缀和吧2333
上代码:
#include<iostream> #include<cstdio> #include<cstdlib> #define LL long long using namespace std; const int maxx = 200003; int n,m,w[maxx],v[maxx],L[maxx],R[maxx]; LL S,num[maxx],sum[maxx]; int l=1e7,r=0; LL Lmin(LL a,LL b) { return a > b ? b : a; } int max(int a,int b) { return a > b ? a : b; } LL check(int x) { LL YY=0; for(int i=1; i<=n; i++) { sum[i]=sum[i-1]; num[i]=num[i-1]; if(w[i]>=x) sum[i]+=v[i],num[i]++; } for(int i=1; i<=m; i++) { LL tot_weight = sum[R[i]] - sum[L[i]-1]; LL tot_num = num[R[i]] - num[L[i]-1]; YY+=tot_weight * tot_num; } return YY; } void works() { int mid; LL ans = 1e11; while(l<=r) { mid = (l+r)>>1; LL Y = check(mid); if(Y < S) r = mid-1; if(Y > S) l = mid+1; if(Y == S) { printf("0 "); return ; } ans = Lmin(ans,abs(S-Y)); } printf("%lld ",ans); } void reads() { scanf("%d%d%lld",&n,&m,&S); for(int i=1; i<=n; i++) scanf("%d%d",&w[i],&v[i]), r=max(r,w[i]),l=min(l,w[i]); for(int i=1; i<=m; i++) scanf("%d%d",&L[i],&R[i]); works(); } int main() { reads(); return 0; }
P1772 [ZJOI2006]物流运输
题目描述
物流公司要把一批货物从码头A运到码头B。由于货物量比较大,需要n天才能运完。货物运输过程中一般要转停好几个码头。物流公司通常会设计一条固定的运输路线,以便对整个运输过程实施严格的管理和跟踪。由于各种因素的存在,有的时候某个码头会无法装卸货物。这时候就必须修改运输路线,让货物能够按时到达目的地。但是修改路线是—件十分麻烦的事情,会带来额外的成本。因此物流公司希望能够订一个n天的运输计划,使得总成本尽可能地小。
输入输出格式
输入格式:
第一行是四个整数n(l≤n≤100)、m(l≤m≤20)、K和e。n表示货物运输所需天数,m表示码头总数,K表示每次修改运输路线所需成本。接下来e行每行是一条航线描述,包括了三个整数,依次表示航线连接的两个码头编号以及航线长度(>0)。其中码头A编号为1,码头B编号为m。单位长度的运输费用为1。航线是双向的。再接下来一行是一个整数d,后面的d行每行是三个整数P(1<P<m),a,b(1≤a≤b≤n)。表示编号为P的码头从第a天到第b天无法装卸货物(含头尾)。同一个码头有可能在多个时间段内不可用。但任何时间都存在至少一条从码头A到码头B的运输路线。
输出格式:
包括了一个整数表示最小的总成本。总成本=n天运输路线长度之和+K*改变运输路线的次数。
输入输出样例
5 5 10 8 1 2 1 1 3 3 1 4 2 2 3 2 2 4 4 3 4 1 3 5 2 4 5 2 4 2 2 3 3 1 1 3 3 3 4 4 5
32
说明
【样例输入说明】
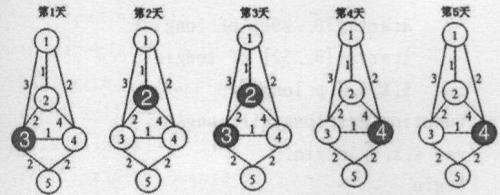
上图依次表示第1至第5天的情况,阴影表示不可用的码头。
【样例输出说明】
前三天走1-4-5,后两天走1-3-5,这样总成本为(2+2)*3+(3+2)*2+10=32。
_NOI导刊2010提高(01)
思路:
spfa+dp
f[i]表示到第i天的最小花费
cost[i][j] 表示从第i天到第j天可行的最短路,由于数据范围很小,可以预处理cost
状态转移方程 f[i] = min { f[j] + cost[j+1][i] * (i-j) + k} (0<=j<i)
上代码:
#include<algorithm> #include<iostream> #include<cstring> #include<cstdio> #include<queue> using namespace std; const int INF=1e9; int n,m,k,e,num_edge,head[1101],d,x,y,z; struct Edge{ int pre,to,w; }edge[1101]; int dis[101],cost[110][110],f[110]; bool pd[25][110],vis[110]; queue<int>q; void add(int u,int v,int w) { edge[++num_edge].pre = head[u]; edge[num_edge].to = v; edge[num_edge].w = w; head[u] = num_edge; } int had(int num,int l,int r) { for(int i=l; i<=r; i++) if(pd[num][i]) return false; return true; } int spfa(int a,int b) { if(!had(1,a,b)) return INF; memset(vis,0,sizeof(vis)); while(!q.empty()) q.pop(); for(int i=1; i<=m; i++) dis[i]=INF; q.push(1); vis[1]=true; dis[1]=0; while(!q.empty()) { int u=q.front(); q.pop(); for(int i=head[u]; i ; i=edge[i].pre) { int w=edge[i].w, v=edge[i].to; if(!had(v,a,b)) continue; if(dis[v]>dis[u]+w) { dis[v] = dis[u]+w; if(!vis[v]) { q.push(v); vis[u] = true; } } } vis[u] = false; } if(dis[m]==INF) return INF; else return dis[m]*(b-a+1); } int main() { scanf("%d%d%d%d",&n,&m,&k,&e); for(int i=1; i<=e; i++) { scanf("%d%d%d",&x,&y,&z); add(x,y,z); add(y,x,z); } scanf("%d",&d); for(int i=1; i<=d; i++) { int l,r; scanf("%d%d%d",&x,&l,&r); for(int j=l; j<=r; j++) pd[x][j] = true; } for(int i=1; i<=n; i++) for(int j=i; j<=n; j++) cost[i][j]=spfa(i,j); f[0]=0; for(int i=1; i<=n; i++) f[i] = cost[1][i]; for(int i=2; i<=n; i++) for(int j=i-1; j>=1; --j) if(cost[j+1][i]!=INF) f[i]=min(f[i],f[j]+cost[j+1][i]+k); else break; printf("%d",f[n]); return 0; }
P2285 [HNOI2004]打鼹鼠
题目描述
鼹鼠是一种很喜欢挖洞的动物,但每过一定的时间,它还是喜欢把头探出到地面上来透透气的。根据这个特点阿牛编写了一个打鼹鼠的游戏:在一个n*n的网格中,在某些时刻鼹鼠会在某一个网格探出头来透透气。你可以控制一个机器人来打鼹鼠,如果i时刻鼹鼠在某个网格中出现,而机器人也处于同一网格的话,那么这个鼹鼠就会被机器人打死。而机器人每一时刻只能够移动一格或停留在原地不动。机器人的移动是指从当前所处的网格移向相邻的网格,即从坐标为(i,j)的网格移向(i-1, j),(i+1, j),(i,j-1),(i,j+1)四个网格,机器人不能走出整个n*n的网格。游戏开始时,你可以自由选定机器人的初始位置。
现在知道在一段时间内,鼹鼠出现的时间和地点,请编写一个程序使机器人在这一段时间内打死尽可能多的鼹鼠。
输入输出格式
输入格式:
从文件input.txt中读入数据,文件第一行为n(n<=1000), m(m<=10000),其中m表示在这一段时间内出现的鼹鼠的个数,接下来的m行中每行有三个数据time,x,y表示有一只鼹鼠在游戏开始后time个时刻,在第x行第y个网格里出现了一只鼹鼠。Time按递增的顺序给出。注意同一时刻可能出现多只鼹鼠,但同一时刻同一地点只可能出现一只鼹鼠。
输出格式:
输出文件output.txt中仅包含一个正整数,表示被打死鼹鼠的最大数目。
输入输出样例
2 2 1 1 1 2 2 2
1
思路:
i枚举鼹鼠,j枚举之后的鼹鼠,j鼹鼠要在自己和i鼹鼠+1(原来鼹鼠+新打死的鼹鼠)之间取max
因为time按递增顺序排序,j从i+1枚举,保证times[j]-times[i]>=0;
答案是取最大。。。
上代码:
#include<iostream> #include<cstdio> #include<cstdlib> using namespace std; const int M = 10010; int n,m,times[M],x[M],y[M]; int f[M],ans; int main() { scanf("%d%d",&n,&m); for(int i=1; i<=m; i++) { scanf("%d%d%d",×[i],&x[i],&y[i]); f[i]=1; } for(int i=1; i<=m; i++) { for(int j=i+1; j<=m; j++) if(abs(x[i]-x[j])+abs(y[i]-y[j])<=times[j]-times[i]) f[j]=max(f[j],f[i]+1); ans=max(ans,f[i]); } printf("%d",ans); return 0; }
P3203 [HNOI2010]BOUNCE 弹飞绵羊
题目描述
某天,Lostmonkey发明了一种超级弹力装置,为了在他的绵羊朋友面前显摆,他邀请小绵羊一起玩个游戏。游戏一开始,Lostmonkey在地上沿着一条直线摆上n个装置,每个装置设定初始弹力系数ki,当绵羊达到第i个装置时,它会往后弹ki步,达到第i+ki个装置,若不存在第i+ki个装置,则绵羊被弹飞。绵羊想知道当它从第i个装置起步时,被弹几次后会被弹飞。为了使得游戏更有趣,Lostmonkey可以修改某个弹力装置的弹力系数,任何时候弹力系数均为正整数。
输入输出格式
输入格式:
第一行包含一个整数n,表示地上有n个装置,装置的编号从0到n-1,接下来一行有n个正整数,依次为那n个装置的初始弹力系数。第三行有一个正整数m,接下来m行每行至少有两个数i、j,若i=1,你要输出从j出发被弹几次后被弹飞,若i=2则还会再输入一个正整数k,表示第j个弹力装置的系数被修改成k。对于20%的数据n,m<=10000,对于100%的数据n<=200000,m<=100000
输出格式:
对于每个i=1的情况,你都要输出一个需要的步数,占一行。
输入输出样例
4 1 2 1 1 3 1 1 2 1 1 1 1
2 3
思路:
分块思想。。。
上代码:
#include<iostream> #include<cmath> #include<cstdio> #include<cstdlib> using namespace std; /* sizes表示块的大小 num表示块的个数 belong[i]表示第i个点在第几个块里 l[i]表示第i块的左边界的坐标 r[i]表示第i块的左边界的坐标 step[i]表示从i跳当前块还需要几步 nxt[i]表示下一步到达的点 */ const int M = 200010; int n,k[M]; int sizes,num,belong[M],l[1000],r[1000],step[M],nxt[M],m; void handle() { sizes=sqrt(n); num=sizes; if(n%num) num++; for(int i=0; i<n; i++) belong[i]=(i-1)/sizes; for(int i=1; i<=num; i++) { l[i]=(i-1)*sizes; r[i]=i*sizes-1; } r[num]=n; for(int i=n-1; i>=0; i--) { int now = i+k[i]; if(now>=n) step[i]=1,nxt[i]=-1; else { if(belong[i]==belong[now]) { step[i]=step[now]+1;//now在i之后,倒叙枚举now先处理,如果从now跳一步出界,从i跳一步到now,那么从i跳出界为now+1 nxt[i]=nxt[now]; //step[i]记录的是从i跳几步会跳出当前块 把大区间转换成一块一块来处理 所以now和i不属于同一块意思就是从i点一步就可以跳出所在块 所以等于1 } else { step[i]=1; nxt[i]=now; } } } } int cale(int pos) { int ans=0; while(pos!=-1) { ans+=step[pos]; pos=nxt[pos]; } return ans; } int main() { scanf("%d",&n); for(int i=0; i<n; i++) scanf("%d",&k[i]); handle(); scanf("%d",&m); for(int i=1; i<=m; i++) { int type; scanf("%d",&type); if(type==1) { int j; scanf("%d",&j); printf("%d ",cale(j)); } else { int a,b; scanf("%d%d",&a,&b); k[a]=b; for(int i=a; i>=l[belong[a]]; i--) { int now = i+k[i]; if(now>=n) step[i]=1,nxt[i]=-1; else { if(belong[i]==belong[now]) { step[i]=step[now]+1;//now在i之后,倒叙枚举now先处理,如果从now跳一步出界,从i跳一步到now,那么从i跳出界为now+1 nxt[i]=nxt[now]; //step[i]记录的是从i跳几步会跳出当前块 把大区间转换成一块一块来处理 所以now和i不属于同一块意思就是从i点一步就可以跳出所在块 所以等于1 } else { step[i]=1; nxt[i]=now; } } } } } return 0; }
自己选的路,跪着也要走完!!!