P1379 八数码难题
题目描述
在3×3的棋盘上,摆有八个棋子,每个棋子上标有1至8的某一数字。棋盘中留有一个空格,空格用0来表示。空格周围的棋子可以移到空格中。要求解的问题是:给出一种初始布局(初始状态)和目标布局(为了使题目简单,设目标状态为123804765),找到一种最少步骤的移动方法,实现从初始布局到目标布局的转变。
输入输出格式
输入格式:
输入初始状态,一行九个数字,空格用0表示
输出格式:
只有一行,该行只有一个数字,表示从初始状态到目标状态需要的最少移动次数(测试数据中无特殊无法到达目标状态数据)
输入输出样例
283104765
4
题解:
bfs
代码:

#include<map> #include<cstdio> #include<iostream> using namespace std; const int M = 5000010; char s; string cs; int a[M][5][5],b[M][5]; int dx[4]= {1,0,-1,0}, dy[4]= {0,1,0,-1}; int bfs() { map<string,int>mm; register int head=0,tail=1,xx,yy; b[1][3]=1; do { head++; for(register int i=0; i<4; i++) { xx = b[head][1]+dx[i]; yy = b[head][2]+dy[i]; if(xx>0&&xx<4&&yy>0&&xx<4) { tail++; b[tail][1]=xx; b[tail][2]=yy; b[tail][3]=b[head][3]+1; for(register int q=1; q<=3; q++) for(register int j=1; j<=3; j++) a[tail][q][j]=a[head][q][j]; cs=" ";//重置cs字符串 swap(a[tail][b[head][1]][b[head][2]],a[tail][xx][yy]);//将0和另一个搜索到的数交换 cs+=(char)a[tail][1][1]+'A'; cs+=(char)a[tail][1][2]+'A'; cs+=(char)a[tail][1][3]+'A'; cs+=(char)a[tail][2][1]+'A'; cs+=(char)a[tail][2][2]+'A'; cs+=(char)a[tail][2][3]+'A'; cs+=(char)a[tail][3][1]+'A'; cs+=(char)a[tail][3][2]+'A'; cs+=(char)a[tail][3][3]+'A'; if(mm[cs]) { tail--; continue; } mm[cs]=1; if(a[tail][1][1]==1 && a[tail][1][2]==2 && a[tail][1][3]==3 && a[tail][2][1]==8 && a[tail][2][2]==0 && a[tail][2][3]==4 && a[tail][3][1]==7 && a[tail][3][2]==6 && a[tail][3][3]==5) return b[head][3]; } } } while(head<tail); return 0; } int main() { for(register int i=1; i<=3; i++) { for(register int j=1; j<=3; j++) { cin>>s; a[1][i][j]=s-'0';//转换成数字,存入三维数组 if(a[1][i][j]==0) { b[1][1]=i;//寻找0的位置,进入队列 b[1][2]=j; } } } printf("%d",bfs()); return 0; }
P1312 Mayan游戏
题目描述
Mayan puzzle是最近流行起来的一个游戏。游戏界面是一个 7 行5 列的棋盘,上面堆放着一些方块,方块不能悬空堆放,即方块必须放在最下面一行,或者放在其他方块之上。游戏通关是指在规定的步数内消除所有的方块,消除方块的规则如下:
1 、每步移动可以且仅可以沿横向(即向左或向右)拖动某一方块一格:当拖动这一方块时,如果拖动后到达的位置(以下称目标位置)也有方块,那么这两个方块将交换位置(参见输入输出样例说明中的图6 到图7 );如果目标位置上没有方块,那么被拖动的方块将从原来的竖列中抽出,并从目标位置上掉落(直到不悬空,参见下面图1 和图2);
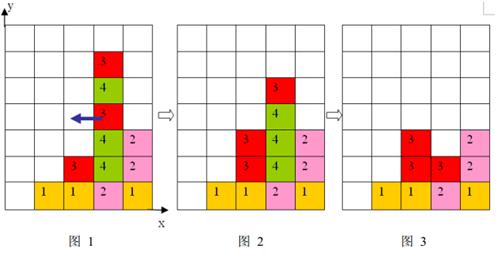
2 、任一时刻,如果在一横行或者竖列上有连续三个或者三个以上相同颜色的方块,则它们将立即被消除(参见图1 到图3)。
注意:
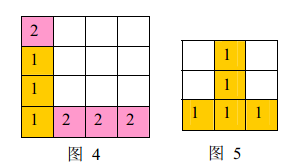
a) 如果同时有多组方块满足消除条件,几组方块会同时被消除(例如下面图4 ,三个颜色为1 的方块和三个颜色为 2 的方块会同时被消除,最后剩下一个颜色为 2 的方块)。
b) 当出现行和列都满足消除条件且行列共享某个方块时,行和列上满足消除条件的所有方块会被同时消除(例如下面图5 所示的情形,5 个方块会同时被消除)。
3 、方块消除之后,消除位置之上的方块将掉落,掉落后可能会引起新的方块消除。注意:掉落的过程中将不会有方块的消除。
上面图1 到图 3 给出了在棋盘上移动一块方块之后棋盘的变化。棋盘的左下角方块的坐标为(0, 0 ),将位于(3, 3 )的方块向左移动之后,游戏界面从图 1 变成图 2 所示的状态,此时在一竖列上有连续三块颜色为4 的方块,满足消除条件,消除连续3 块颜色为4 的方块后,上方的颜色为3 的方块掉落,形成图 3 所示的局面。
输入输出格式
输入格式:
输入文件mayan.in,共 6 行。
第一行为一个正整数n ,表示要求游戏通关的步数。
接下来的5 行,描述 7*5 的游戏界面。每行若干个整数,每两个整数之间用一个空格隔开,每行以一个0 结束,自下向上表示每竖列方块的颜色编号(颜色不多于10种,从1 开始顺序编号,相同数字表示相同颜色)。
输入数据保证初始棋盘中没有可以消除的方块。
输出格式:
输出文件名为mayan.out
如果有解决方案,输出 n 行,每行包含 3 个整数x,y,g ,表示一次移动,每两个整数之间用一个空格隔开,其中(x ,y)表示要移动的方块的坐标,g 表示移动的方向,1 表示向右移动,-1表示向左移动。注意:多组解时,按照 x 为第一关健字,y 为第二关健字,1优先于-1 ,给出一组字典序最小的解。游戏界面左下角的坐标为(0 ,0 )。
如果没有解决方案,输出一行,包含一个整数-1。
输入输出样例
3
1 0
2 1 0
2 3 4 0
3 1 0
2 4 3 4 0
2 1 1
3 1 1
3 0 1
说明
【输入输出样例说明】
按箭头方向的顺序分别为图6 到图11
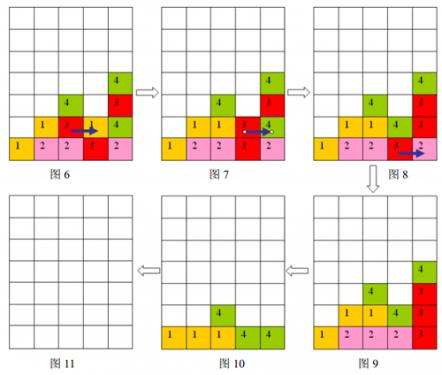
样例输入的游戏局面如上面第一个图片所示,依次移动的三步是:(2 ,1 )处的方格向右移动,(3,1 )处的方格向右移动,(3 ,0)处的方格向右移动,最后可以将棋盘上所有方块消除。
【数据范围】
对于30% 的数据,初始棋盘上的方块都在棋盘的最下面一行;
对于100%的数据,0 < n≤5 。
noip2011提高组day1第3题
题解:
按照题目描述进行搜索,考虑如何实现,交换(带色格和带色格交换、带色格和空白格交换)和下落
代码:

#include<cmath> #include<cstdio> #include<cstring> #include<cstdlib> #include<iostream> #define max(x,y) ((x)<(y)?(y):(x)) #define min(x,y) ((x)<(y)?(x):(y)) using namespace std; int a[8][6],t[10][3]; int n; bool vis[8][6]; void init() { scanf("%d",&n); int x,now=1; for(int i=1; i<=5; i++) { now=1; while(scanf("%d",&x)==1 && x!=0) a[now++][i]=x; } } int flag1,flag2; inline int check() { flag1=flag2=0; memset(vis,0,sizeof(vis)); for(int i=1; i<=7; i++) for(int j=1; j<=5; j++) { if(a[i][j]) flag1=1;//f1判断是否存在有颜色的格子 if(j<=3&&a[i][j]&&a[i][j]==a[i][j+1]&&a[i][j]==a[i][j+2]) vis[i][j]=vis[i][j+1]=vis[i][j+2]=1,flag2=1; //三个横排连着 if(i<=5&&a[i][j]&&a[i][j]==a[i+1][j]&&a[i][j]==a[i+2][j]) vis[i][j]=vis[i+1][j]=vis[i+2][j]=1,flag2=1; //三个竖排连着 } if(flag1==0) return 10; return flag2; } inline void print(int step) {//记录交换 for(int i=1; i<=step; i++) printf("%d %d %d ",t[i][1],t[i][2],t[i][0]); exit(0); } inline void ans(int x,int y,int g,int step) { t[step][1]=y-1,t[step][2]=x-1,t[step][0]=g; return ; } inline void down() {//下落 for(int i=1; i<=7; i++) for(int j=1; j<=5; j++) if(vis[i][j]) a[i][j]=0;//除去已经消除的方格的颜色 for(int j=1; j<=5; j++) for(int i=1; i<=7; i++) { if(!a[i][j]) for(int k=i+1; k<=7; k++) { if(a[k][j]) { a[i][j]=a[k][j]; a[k][j]=0; break; } } } } inline void move(int x,int y,int g) {//交换两个方格 swap(a[x][y],a[x][y+g]); memset(vis,0,sizeof(vis)); down();//处理下落情况 while(check()==1) down();//如果有三个连通,消去,并下落 } int cnt[10]; inline void dfs(int step) { if(check()==10) print(step); if(step>=n) return; int b[8][6]; memcpy(b,a,sizeof b); memset(cnt,0,sizeof cnt); for(int i=1; i<=7; i++) for(int j=1; j<=5; j++) cnt[a[i][j]]++;//cnt[i]存颜色为i的格子总数 for(int i=1; i<=10; i++) if(cnt[i]==1 || cnt[i]==2) return;//如果存在一种颜色的格子<3,那么一定不能完全消掉 for(int j=1; j<=5; j++) for(int i=1; i<=7; i++) { if(!a[i][j]) continue;//如果是空格子,跳过 if(j!=5 && a[i][j]!=a[i][j+1]) { //可交换 ans(i,j,1,step+1); move(i,j,1); dfs(step+1); memcpy(a,b,sizeof a); } if(j!=1 && !a[i][j-1]) { //与空白格交换 ans(i,j,-1,step+1); move(i,j,-1); dfs(step+1); memcpy(a,b,sizeof b); } } } int main() { init(); dfs(0); printf("-1 "); }
P2296 寻找道路
题目描述
在有向图G 中,每条边的长度均为1 ,现给定起点和终点,请你在图中找一条从起点到终点的路径,该路径满足以下条件:
1 .路径上的所有点的出边所指向的点都直接或间接与终点连通。
2 .在满足条件1 的情况下使路径最短。
注意:图G 中可能存在重边和自环,题目保证终点没有出边。
请你输出符合条件的路径的长度。
输入输出格式
输入格式:
输入文件名为road .in。
第一行有两个用一个空格隔开的整数n 和m ,表示图有n 个点和m 条边。
接下来的m 行每行2 个整数x 、y ,之间用一个空格隔开,表示有一条边从点x 指向点y 。
最后一行有两个用一个空格隔开的整数s 、t ,表示起点为s ,终点为t 。
输出格式:
输出文件名为road .out 。
输出只有一行,包含一个整数,表示满足题目᧿述的最短路径的长度。如果这样的路径不存在,输出- 1 。
输入输出样例
3 2
1 2
2 1
1 3
-1
6 6
1 2
1 3
2 6
2 5
4 5
3 4
1 5
3
说明
解释1:
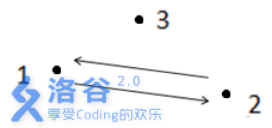
如上图所示,箭头表示有向道路,圆点表示城市。起点1 与终点3 不连通,所以满足题
目᧿述的路径不存在,故输出- 1 。
解释2:
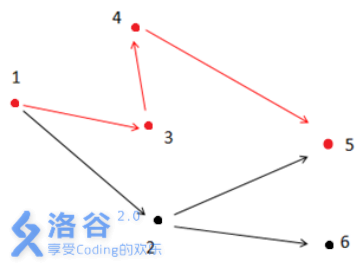
如上图所示,满足条件的路径为1 - >3- >4- >5。注意点2 不能在答案路径中,因为点2连了一条边到点6 ,而点6 不与终点5 连通。
对于30%的数据,0<n≤10,0<m≤20;
对于60%的数据,0<n≤100,0<m≤2000;
对于100%的数据,0<n≤10,000,0<m≤200,000,0<x,y,s,t≤n,x≠t。
题解:
图上搜索
反向bfs(判断是否与终点连通)+最短路
代码:

#include<queue> #include<cstdio> #include<cstring> #include<iostream> using namespace std; const int M = 400010; const int N = 10010; int n,m,x,y,head[N],num_edge,s,t,dis[M],vis[M],v[M]; queue<int>q,que; struct Edge{ int from,to,len; }edge[M],e[M]; int h[N],num,numb[N],chu[N]; void add(int u,int v) { edge[++num_edge].from = head[u]; edge[num_edge].to = v; head[u]=num_edge; e[num_edge].from = h[v]; e[num_edge].to = u; h[v]=num_edge; } void bfs(int t) { que.push(t); v[t]=1; while(!que.empty()) { int k=que.front(); que.pop(); for(int j=h[k]; j; j=e[j].from) { int too=e[j].to; numb[too]++;//反向点的入度 if(!v[too]) { v[too]=1; que.push(too); } } } } //反向点的入度 == 正向图的初度 void spfa(int s,int t) { for(int i=1; i<=n; i++) dis[i]=0x7fffffff; dis[s]=0; vis[s]=1; q.push(s); while(!q.empty()) { int k=q.front(); q.pop(); for(int i=head[k]; i; i=edge[i].from) { int v=edge[i].to; if(dis[v]>dis[k]+1 && numb[v]==chu[v]) { //若反向点的入度 == 正向图的初度,说明在反向bfs中,没有筛掉一条边,也就说明改点与终点是连通的 dis[v]=dis[k]+1; if(!vis[v]) { vis[v]=1; q.push(v); } } } } if(dis[t]==0x7fffffff) printf("-1"); else printf("%d",dis[t]); } int main() { scanf("%d%d",&n,&m); for(int i=1; i<=m; i++) { scanf("%d%d",&x,&y); add(x,y); chu[x]++;//正向图的初度 }; scanf("%d%d",&s,&t); bfs(t); spfa(s,t); return 0; }
自己选的路,跪着也要走完!!!
