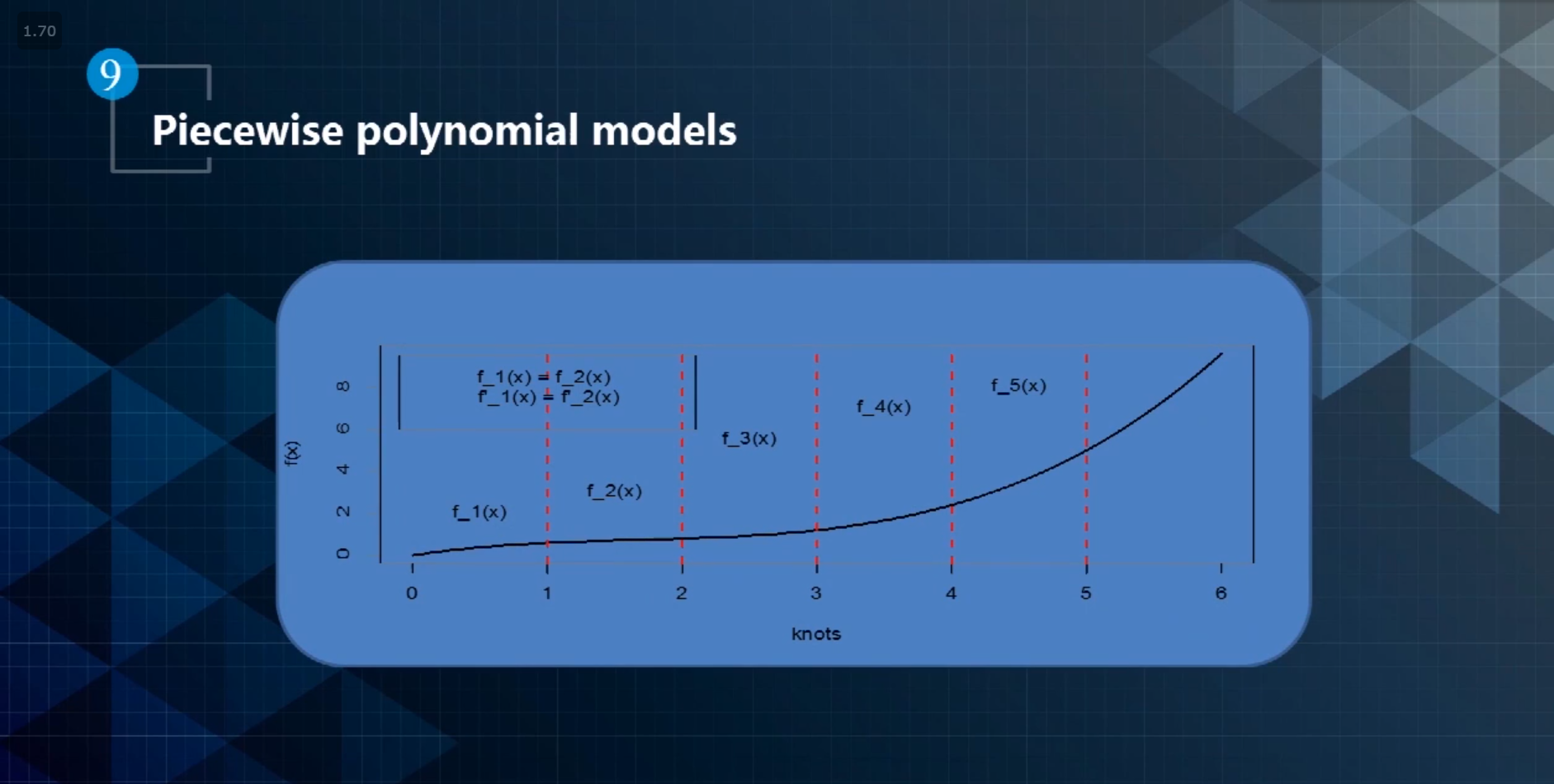
运动规划
与环境相结合
1.建立车辆模型
2.将运动规划与车辆模型结合
如何去表示一个曲线的走向?
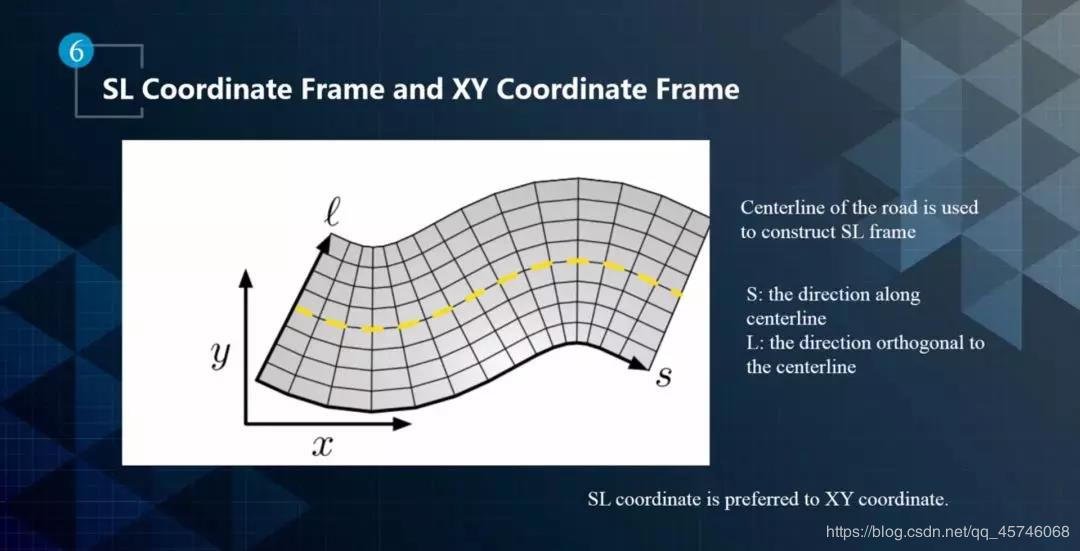
找出其方程表示:坐标系可以使用XY坐标系和SL坐标系
SL坐标系也叫做frenet frame:它以道路中心线为参考,S表示道路中心线的方向,L表示与道路中心线垂直的方向。
在结构化道路上行驶的时候,SL坐标系比XY坐标系更加贴合实际需求。
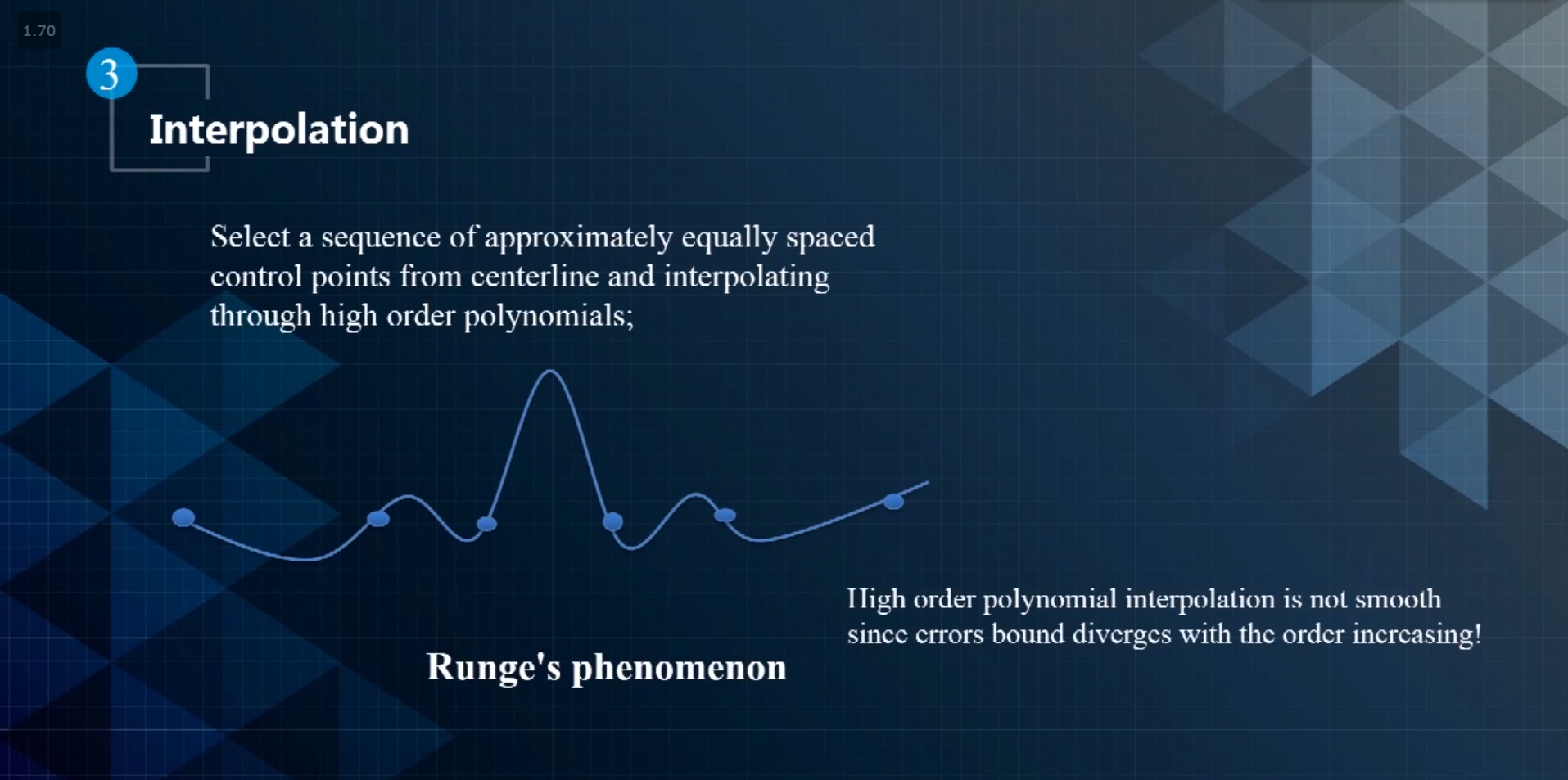
Interpolation
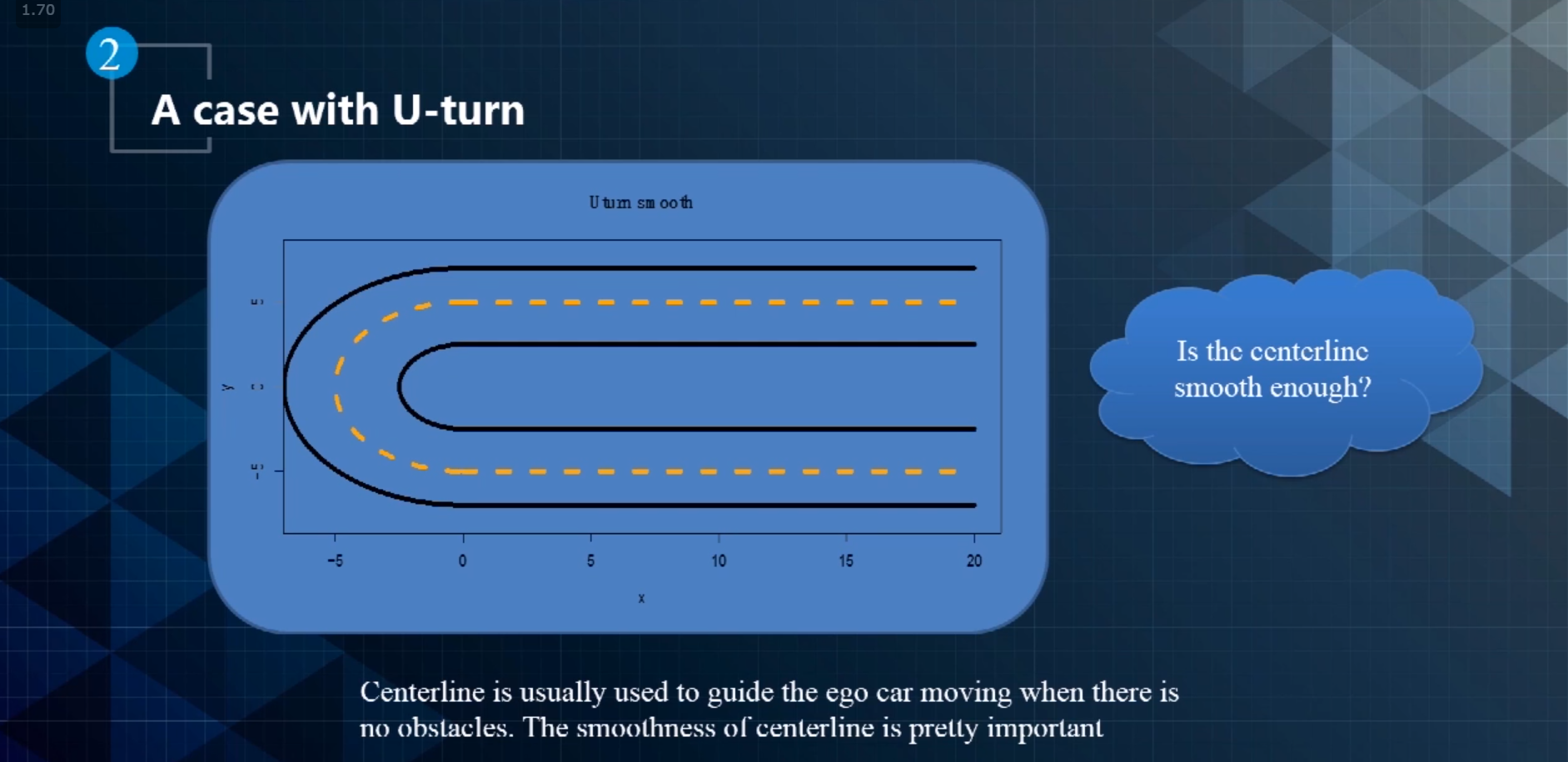
U型弯道举例:
- 在轨迹上以等距离的方式随机选择一些点,然后用高阶多项插值的方式来近似表示轨迹,对多项式进行优化。但是高阶多项式不能用于平滑,因为高阶的多项式抖动太大,没有办法控制幅度,这就是常说的龙格现象
Bezier Spline
Bezier Spline 曲线是由一系列控制点定义的,例如 到 ,其中 n 代表曲线的阶数。如下图所示,分别给出 1 阶、2 阶、3 阶 Bezier Spline 曲线的表示形式。通过对它们做平滑,得到平滑的曲线,例如二阶平滑保证曲线的曲率平滑。但是这种方法的缺点是,除了起始点和终点,其它控制点不能保证会被得到的曲线经过。


精确的模型举例:
Spline 2D
注意旋转不变性
螺旋曲线spiral path——通过极坐标的形式定义(满足起点和终点的约束)

Spline 2D 与Spiral Path的区别
Spiral Path 和 Spline 2D 有什么区别呢?任何的曲线在足够密的时候都可以用Piecewise Spiral path 或者是 Piecewise Polynomial 表示。但是它们的出发点不一样,Polynomial 计算很快很简单,Spline 2D 是一个凸空间里面生成一个 Spline 曲线。Spiral Path 是从 Configuration Space 出发。理论上来讲,螺旋曲线生成的线是要比 Spline 更好处理,对一些极端情况处理更好。