P2331 [SCOI2005]最大子矩阵

在 @[hs巨佬](https://www.cnblogs.com/FloraLOVERyuuji/) 的提醒下, 发现本题还可以暴力的 $O(N^3)$ 转移, 但是我太菜了, 没想出来, 只想出来$O(N^2)$的麻烦的转移方法,,,

---

分析一下, 发现当前一行的转移可以只和上一行的状态有关, 当然, 状态有些复杂. 于是拿出纸笔分析一下.
一开始以为只有这四种情况: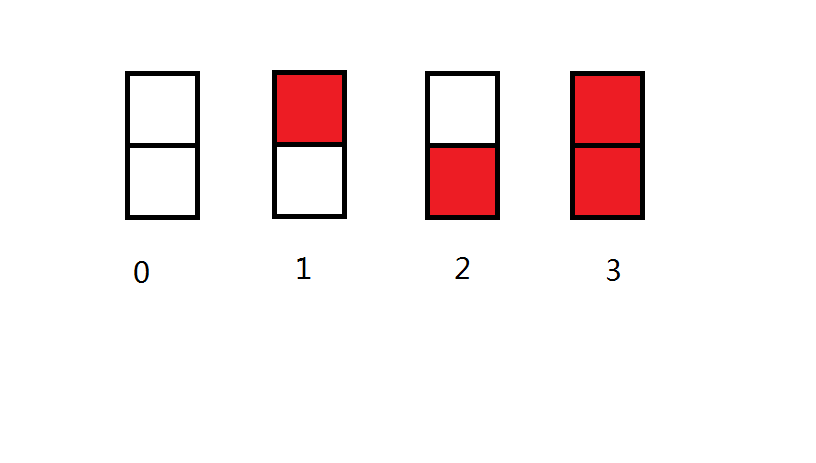

结果交上去WA了好几发,,,

实际上, 情况(3)没有那么简单. 这个上下都涂色的方案应该有两种小情况, 分别是: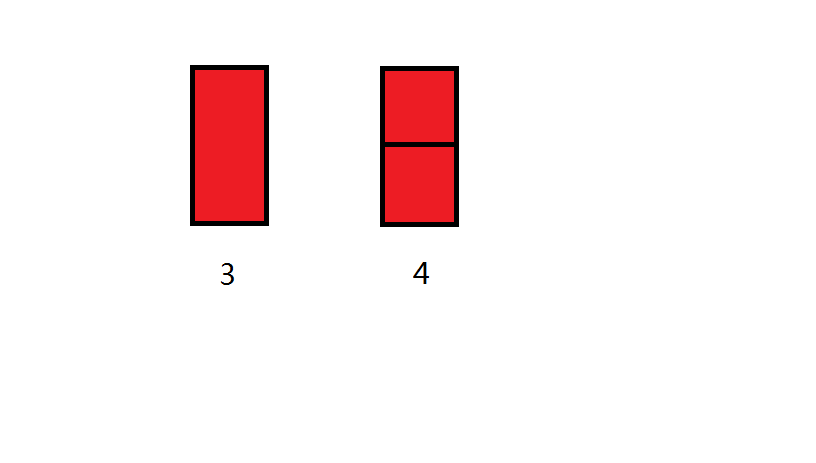

一种是竖着的一个矩形, 一种是横着的跟前面拼起来的两个小矩形. 易证这两种情况完全不同.
所以说, 以后分析的时候一定要细致, 不能只看图的啊,,,

#include <cstdio>
#include <cstring>
#include <cassert>
#include <iostream>
#include <algorithm>
using namespace std;
const int MAXN = 1e2 + 10;
const int MAXK = 10 + 2;
inline int read()
{
    int x = 0; char ch = getchar(); bool flag = false;
    while(!isdigit(ch)) flag |= (ch == '-'), ch = getchar();
    while(isdigit(ch)) x = x * 10 + ch - '0', ch = getchar();
    return flag ? -x : x;
}

int N, M, K;
int a[MAXN][2], sum[MAXN][2];
int f[MAXN][MAXK][5];

int main()
{
    cin>>N>>M>>K;
    for(int i = 1; i <= N; i++)
        for(int j = 1; j <= M; j++) a[i][j] = read();
    for(int i = 1; i <= N; i++)
        for(int j = 1; j <= M; j++) sum[i][j] = sum[i - 1][j] + a[i][j];

    if(M == 1){
        for(int i = 1; i <= N; i++)
            for(int k = 1; k <= K; k++){
                f[i][k][0] = max(f[i - 1][k][0], f[i - 1][k][1]);
                f[i][k][1] = max(f[i - 1][k - 1][0], f[i - 1][k][1]) + a[i][1];
            }
        cout<<max(f[N][K][0], f[N][K][1])<<endl;
    }
    else {
        memset(f, -0x3f, sizeof(f));
        for(int i = 0; i <= N; i++)
            for(int j = 0; j <= K; j++) f[i][j][0] = 0;
                
        for(int i = 1; i <= N; i++)
            for(int k = 1; k <= K; k++){
                f[i][k][0] = max(max(max(f[i - 1][k][0], f[i - 1][k][1]), max(f[i - 1][k][2], f[i - 1][k][3])), f[i - 1][k][4]);
                f[i][k][1] = max(max(max(f[i - 1][k - 1][0], f[i - 1][k][1]), max(f[i - 1][k - 1][2], f[i - 1][k - 1][3])), f[i - 1][k][4]) + a[i][1];
                f[i][k][2] = max(max(max(f[i - 1][k - 1][0], f[i - 1][k - 1][1]), max(f[i - 1][k][2], f[i - 1][k - 1][3])), f[i - 1][k][4]) + a[i][2];
                f[i][k][3] = max(max(max(f[i - 1][k - 1][0], f[i - 1][k - 1][1]), max(f[i - 1][k - 1][2], f[i - 1][k][3])), f[i - 1][k - 1][4]) + a[i][1] + a[i][2];
                f[i][k][4] = max(max(f[i - 1][k - 1][1], f[i - 1][k - 1][2]), f[i - 1][k][4]) + a[i][1] + a[i][2];
                if(k >= 2) f[i][k][4] = max(f[i][k][4], max(f[i - 1][k - 2][3], f[i - 1][k - 2][0]) + a[i][1] + a[i][2]);
            }
        cout<<max(max(max(f[N][K][0], f[N][K][1]), max(f[N][K][2], f[N][K][3])), f[N][K][4])<<endl;
    }
    return 0;
}