P2216 [HAOI2007]理想的正方形

这个题以前做过但是没有写出来, 今天又想了一下, 做出来了. 首先考虑暴力. 考虑枚举每个矩形的右下角, 然后暴力 $O(N^2)$ 转移, 总体复杂度是 $O(ABN^2)$ 的. 观察重复计算的区域: 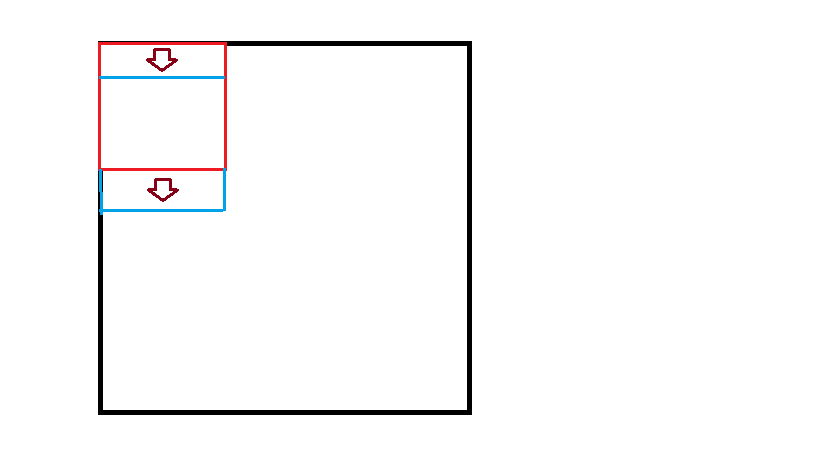 考虑从红色矩形转移到蓝色矩形, 很明显红蓝重合的一部分是可以重复利用的. 横向也是一个道理. 关于如何重复利用, 有很多人是利用单调队列来处理的, 但是我感觉有点麻烦, 就牺牲了 $O(logN)$ 的复杂度, 用`multiset`来处理. 具体来说, 对每一行开一个`multiset`, 每次列变化的时候维护里面的元素, 这样就能很快的求出当前矩阵的最大, 最小值. 这样, 时间复杂度为 $O(kABlogN)$, 理论可以通过. 顺便吐槽一句, `multiset`的常数有点大啊, 开了 $O2$ 才艹过去,,,

#include <set>
#include <cstdio>
#include <cstring>
#include <cassert>
#include <iostream>
#include <algorithm>
using namespace std;
const int MAXN = 1e3 + 10;
inline int read()
{
    int x = 0; char ch = getchar();
    while(!isdigit(ch)) ch = getchar();
    while(isdigit(ch)) x = x * 10 + ch - '0', ch = getchar();
    return x;
}

int A, B, N;
int a[MAXN][MAXN];
multiset<int> S[MAXN];

int main()
{
    cin>>A>>B>>N;
    for(int i = 1; i <= A; i++)
        for(int j = 1; j <= B; j++) a[i][j] = read();

    for(int i = 1; i <= A; i++)
        for(int j = 1; j <= N; j++) S[i].insert(a[i][j]);

    int ans = (1 << 30);
    for(int j = N; j <= B; j++){
        multiset<int> mx, mn;
        for(int i = 1; i <= N; i++) 
            mx.insert(*S[i].rbegin()), mn.insert(*S[i].begin());

        for(int i = N; i <= A; i++) {
            ans = min(ans, *mx.rbegin() - *mn.begin());
            if(i < A){
                mx.insert(*S[i + 1].rbegin()), mn.insert(*S[i + 1].begin());
                mx.erase(mx.find(*S[i - N + 1].rbegin())), mn.erase(mn.find(*S[i - N + 1].begin()));
            }
        }

        if(j < B){
            for(int i = 1; i <= A; i++)
                S[i].insert(a[i][j + 1]), S[i].erase(S[i].find(a[i][j - N + 1]));
        }
    }
    cout<<ans<<endl;
    return 0;
}