返回一个二维整数数组中最大子数组的和

题目:返回一个二维整数数组中最大子数组的和。
要求：
输入一个二维整形数组，数组里有正数也有负数。
数组中连续的一个或多个整数组成一个子数组，每个子数组都有一个和。
求所有子数组的和的最大值。

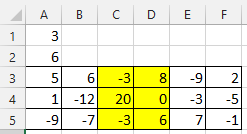
 思路：参考上一次的编程，求的是一维数组中，子数组和的最大值。这次是二维数组，如果将二维数组看作一维数组来解决的话，问题就行的通了。于是，首先要解决的是如何把二维数组当作一维来思考。分析：当最大子数组是一行的话，就直接是上一次的问题，用动态规划即可求出最大子数组的和。若最大子数组是两行时，这时就需要考虑是这两行中的连续的那几列构成的数组之和最大。这时，先把同一列上的元素相加成为一个一维数组，在用动态规划来求出行上最大值数组之和。同理，若最大子数组是三行、四行...n行时，问题就可以解决了。假设输入的是n*m的数组，则时间复杂度为（m*n^2）.

实现代码如下：

//返回一个二位数组中最大子数组的和   2016/4/6 
#include<iostream>
using namespace std;
int dp(int array[],int i)
{
	int dp[100][2],j,S;
	dp[0][0]=array[0];
    dp[0][1]=array[0];
    for(j=1;j<i;j++)
    {
        dp[j][0]=max(dp[j-1][0],dp[j-1][1]);
        
        dp[j][1]=max(array[j],(dp[j-1][1]+array[j]));
    }
    S=max(dp[i-1][0],dp[i-1][1]);
    return S;
}
int main(){
	int Array[100][100],len,wid;
	cin>>len>>wid;
	for(int i=0;i<wid;i++)
	{
		for(int j=0;j<len;j++)
		{
			cin>>Array[i][j];
		}
	}
	int Max[wid],MAX=0;
	for(int i=0;i<wid;i++)
	{
		int temp_Array[len];
		for(int ii=0;ii<len;ii++){
		temp_Array[ii]=Array[i][ii];
		}
		Max[i]=dp(temp_Array,len);
		if(i<len-1)
		{
			for(int count=i+1;count<wid;count++)
			{
				for(int j=0;j<len;j++)
				{
					temp_Array[j]=temp_Array[j]+Array[count][j];
				}
				int temp_max=dp(temp_Array,len);
				Max[i]=max(Max[i],temp_max);
			}
		} 
		MAX=max(MAX,Max[i]);
	}
	cout<<MAX;
	return 0;
} 

运行截图：

总结：一个问题，当有了思路，就成功了一半。有了方向，只管往前走，就可以做到。