首先,建图:建图就是存边;
可以用邻接矩阵,邻接表;但在这篇总结中用vector<int> q[1005];来存储每个节点连接的节点;
其次:图的遍历:DFS,BFS,拓卜排序;
DFS; 栈;
void DFS(int x){
vis[x]=1;
s.push(x);
for(int i=0;i<edge[x].size() ;i++){
if(!vis[edge[x][i]]){
DFS(edge[x][i]);
}
}
}
BFS : 队列;
void BFS(int x){
queue<int> q;
vis2[x]=1;
q.push(x);
while(!q.empty()){
int r=q.front();
for(int i=0;i<point[r].size() ;i++){
if(!vis2[point[r][i]]){
q.push(point[r][i]);
vis2[point[r][i]]=1;
}
}
q.pop();
}
}
拓卜排序:主要是有向图,有先后顺序;循环将入度为0的点入队!
void topo(){
int i;
for(i=1;i<=n;i++){
if(rud[i]==0){
q.push(i);
}
}
while(!q.empty() ){
temp=q.front() ;
q.pop() ;
for(i=0;i<edge[temp].size() ;i++){
t=edge[temp][i];
rud[t]--;
if(rud[t]==0){
q.push(t);
}
}
}
}
例题:
题目描述
一条单向的铁路线上,依次有编号为 1,2,…,n1, 2, …, n 1,2,…,n的 nn n个火车站。每个火车站都有一个级别,最低为 111 级。现有若干趟车次在这条线路上行驶,每一趟都满足如下要求:如果这趟车次停靠了火车站 xxx,则始发站、终点站之间所有级别大于等于火车站x xx 的都必须停靠。(注意:起始站和终点站自然也算作事先已知需要停靠的站点)
例如,下表是5 5 5趟车次的运行情况。其中,前4 44 趟车次均满足要求,而第 555 趟车次由于停靠了 333 号火车站(222 级)却未停靠途经的 666 号火车站(亦为 222 级)而不满足要求。
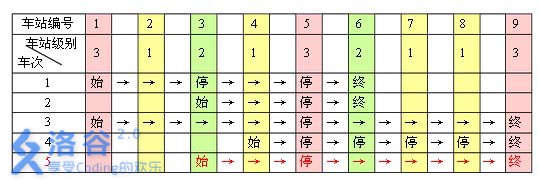
现有 mmm 趟车次的运行情况(全部满足要求),试推算这n nn 个火车站至少分为几个不同的级别。
输入格式
第一行包含 222 个正整数 n,mn, mn,m,用一个空格隔开。
第 i+1i + 1i+1 行(1≤i≤m)(1 ≤ i ≤ m)(1≤i≤m)中,首先是一个正整数 si(2≤si≤n)s_i(2 ≤ s_i ≤ n)si(2≤si≤n),表示第i ii 趟车次有 sis_isi 个停靠站;接下来有si s_isi个正整数,表示所有停靠站的编号,从小到大排列。每两个数之间用一个空格隔开。输入保证所有的车次都满足要求。
输出格式
一个正整数,即 nnn 个火车站最少划分的级别数。
输入输出样例
9 2 4 1 3 5 6 3 3 5 6
2
9 3 4 1 3 5 6 3 3 5 6 3 1 5 9
3
说明/提示
对于20% 20\%20%的数据,1≤n,m≤10
对于 50%50\%50%的数据,1≤n,m≤100
对于 100%100\%100%的数据,1≤n,m≤1000
主要是建图,没有停靠的点小于停靠的点;建一条边;给个下标;
代码:
#include<iostream>
#include<vector>
#include<queue>
#include<string.h>
using namespace std;
int n,m;
int num;
int s;
vector<int> stop;
bool vis[1005];//标记哪些点停;
vector<int> edge[1005];
bool v[1005][1005];//标记是否建边;
int rud[1005];
int ind[1005];
queue<int> q;
int ans;
int t;
int temp;
void topo(){
int i;
for(i=1;i<=n;i++){
if(rud[i]==0){
q.push(i);
}
}
while(!q.empty() ){
temp=q.front() ;
q.pop() ;
for(i=0;i<edge[temp].size() ;i++){
t=edge[temp][i];
rud[t]--;
ind[t]=ind[temp]+1;
if(rud[t]==0){
q.push(t);
ans=max(ans,ind[t]);
}
}
}
}
int main(){
cin>>n>>m;
for(int i=0;i<m;i++){
cin>>num;
stop.clear() ;
memset(vis,0,sizeof(vis));
for(int j=0;j<num;j++){
cin>>s;
stop.push_back(s);
vis[s]=1;
}
for(int j=stop[0];j<stop[num-1];j++){
if(!vis[j]){
for(int k=0;k<num;k++){
if(!v[j][stop[k]]){
edge[j].push_back(stop[k]);
rud[stop[k]]++;
v[j][stop[k]]=1;
}
}
}
}
}
topo();
cout<<ans+1<<endl;
}