Binary Tree Maximum Path Sum

Given a binary tree, find the maximum path sum.

The path may start and end at any node in the tree.

For example:
Given the below binary tree,

       1
      / 
     2   3

Return 6.

关键点1：

分析：http://fisherlei.blogspot.com/2013/01/leetcode-binary-tree-maximum-path-sum.html

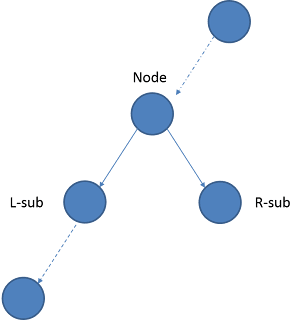
For each node like following, there should be four ways existing for max path:

1. Node only （因为本题中的节点可能是负值！）
2. L-sub + Node
3. R-sub + Node
4. L-sub + Node + R-sub

Keep trace the four path and pick up the max one in the end.  

关键点2：明确递归函数的返回值是什么：这本题中返回值表示通过root节点能走到root的parent的最大和，这个值作为返回对象返给调用父函数。

树结构显然用递归来解，解题关键：

1、对于每一层递归，只有包含此层树根节点的值才可以返回到上层。否则路径将不连续。

2、返回的值最多为根节点加上左右子树中的一个返回值，而不能加上两个返回值。否则路径将分叉。

在这两个前提下有个需要注意的问题，最上层返回的值并不一定是满足要求的最大值，

因为最大值对应的路径不一定包含root的值，可能存在于某个子树上。

因此解决方案为设置全局变量maxSum，在递归过程中不断更新最大值。

参考：http://www.xuebuyuan.com/2102572.html （了解返回值与求得的最大值不是一样的）

因为要计算任意path的最大值， 根据题意要求，可以理解为可以用一笔画完（不重复，不走回头路）的曲线覆盖的节点就算是一条合法的path。

用一个helper函数getSum（TreeNode* root, int &ret）来中序遍历整个tree，这个函数返回值是以root为根的子树的包含root节点本身的一个序列的最大值，ret的值是到遍历完当前root指定的子树后，已经出现过的所有子序列中的最大值； 这样一来，返回至可以被用来继续计算当前root的父亲节点所在的子树的最大值；

这样一来，每处理一个节点的时候可以得到包含其左孩子的一个最大合l，一个包含其右孩子的最大和r， 在考虑节点本身的值val， 我们可以得到4种不同的组合
 (l + val), (r + val), val, (l + val + r),  这四个值取最大的一个来和传入的此前最大的值ret比较并赋值（如果ret小于当前算出的最大值）； 返回值则是max（l, r，0) + val (必须包含当前节点值的一个最大和值)。

C++实现代码：

#include<iostream>
#include<new>
#include<climits>
using namespace std;

//Definition for binary tree
struct TreeNode
{
    int val;
    TreeNode *left;
    TreeNode *right;
    TreeNode(int x) : val(x), left(NULL), right(NULL) {}
};

class Solution
{
public:
    int maxPathSum(TreeNode *root)
    {
        if(root==NULL)
            return 0;
        int res=INT_MIN;
        helper(root,res);
        return res;
    }
    int helper(TreeNode *root,int &res)
    {
        if(root==NULL)
            return 0;
        int left=helper(root->left,res);
        int right=helper(root->right,res);
        int val=root->val;
        if(left>0)
            val+=left;
        if(right>0)
            val+=right;
        int ret=max(root->val,root->val+max(left,right));
        //res指的是所有root中的所有路径的最大值，不一定以root为根，因此不能返回给上层
        res=max(res,max(val,ret));
        //返回值表示的是以root为根的最大值
        return ret;
    }
    void createTree(TreeNode *&root)
    {
        int i;
        cin>>i;
        if(i!=0)
        {
            root=new TreeNode(i);
            if(root==NULL)
                return;
            createTree(root->left);
            createTree(root->right);
        }
    }
};

int main()
{
    Solution s;
    TreeNode *root;
    s.createTree(root);
    cout<<s.maxPathSum(root)<<endl;
}

注意其中ret和res的区别，其实res是包含ret的最大值的，但是res不能用了返回给上层，如果即选择了root的左子树又选择了右子树，则如果返回上层，会出现分支的情况。

简单一点的写法：

class Solution {
public:
    int maxPathSum(TreeNode *root) {
        int ret = INT_MIN;
        getSum(root, ret);
        return ret;
    }
    
private:
    int getSum(TreeNode *node, int &ret) {
        if (node == NULL) return 0;
        int l = getSum(node->left, ret);
        int r = getSum(node->right, ret);
　　　　 //cret是返回值，如果要返回到上层节点root，cret要么是root的左子树与root的和或者是右子树与root的和或者直接就是root的值，取三者中较大的
        int cret = max(node->val, max(l, r) + node->val);
　　　　 //ret维持一个局部的最大值　　
        ret = max(ret, max(cret, l + r + node->val));
        return cret;
    }
};