在移动应用这个行业,国外用户的付费能力是众所周知的,现在很多APP开发商都将市场转向海外。而在海外,用户下载APP的地方只有AppStore和GooglePlay,很多用户都是根据榜单和搜索下载来找到你的应用。那么在AppStore中我们应该如何设置关键字呢?APP覆盖的关键词是否越多越好呢?如何才能提高应用搜索排名呢?
现在有很多的统计工具都可以看见关键字的覆盖率以及关键字的热度。以美团为例,我们可以看到其覆盖大概884个词,这样覆盖词是不是越多越好呢,是否要刻意追求这个数字呢?答案是否定的。
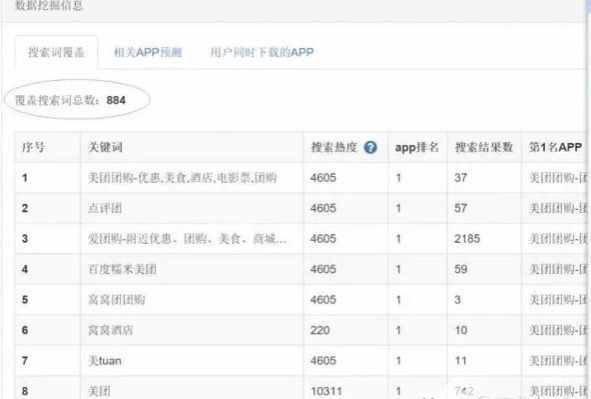
我们先来看看AppStore的关键词命名规则,就知道为什么了?
关键词命中有两种方式,以搜索词“天天飞车”为例:
1.精准匹配。就是你的关键词必须也是“天天飞车”,一模一样的,才能命中。
2.短语匹配。就是可以匹配部分词,或者匹配顺序不一致均可。这种方式一般又分为三种类型:
a,精确包含。即“天天飞车”这个检索词,如关键词为“天天飞车游戏”,“腾讯天天飞车”等形式,都可以名字,因为这些关键词完全包含检索词。
b,同义包含。就是如检索词为“天天飞车”,其分词为“天天”和“飞车”两个词,只要你的关键词包含两个分词即可,不管位置如何。如“天天玩飞车”,“飞车天天跑”,这样的词,都算同义包含,就是包含检索词的所有分词,但位置不一致也可以。
c,核心包含。就是如检索词为“天天飞车”的,其分词为“天天”和“飞车”,则两个词中的一个词命中即可,如”天天“为这个检索的核心词,app的一个关键词为“天天”,则搜索“天天飞车”就能命中这个app,这就算核心包含。当然究竟哪个是核心词,就要看经验判断。换个角度来看,如果填写了“天天”这个关键词,“天天飞车”也能搜到你的app,也算你app覆盖的搜索词。这就是为什么大家都只能写100个字符,而有的app却能覆盖上万个搜索词的关键原因。
熟悉百度广告的童靴可以发现,这个匹配方式和百度搜索广告匹配是基本类似的。具体介绍:
其实,大部分搜索系统均是如此,知道了这一点,理论上你可以造无数个关键词覆盖,如利用核心匹配,添加”助手“这样一个关键词,然后造很多”助手飞车“,”助手我爱“之类的基本没人搜的词,也都能命中你的app,增加2个这样的覆盖词,显然意义不是很大。
因此,看aso的效果,关键还是看搜索词本身的热度,还有你的app的排序位置,一般可用”搜索曝光度“这个指标来衡量。如果清楚了搜索的规则,就自然明白,只看关键词的覆盖数目意义不是很大。当然,也可以做个参考,但不要刻意追求这个数字。
然后根据这个命中规则,也可以清楚的了解所谓的“组词”技术的原理,如你填了两个关键词“腾讯新闻”,“网易新闻”,因为有共同的词“新闻”,因此,可以合并成“腾讯网易新闻”,这样就省下一个词的位置。
用户输入“网易新闻”,也可以命中“腾讯网易新闻”,属于短语匹配–>精确包含。而用户输入“腾讯新闻”,也可以命中“腾讯网易新闻”,就是属于短语匹配–>同义包含。但如果不合并,命中就属于精准匹配。
按照一般的常识,精准匹配肯定是要比短语匹配效果好,得分高。根据我们了解到的,大部分搜索系统中,如果精准匹配算1分的话,短语匹配会有个降权系数,如只能得0.9分,这个取决于具体的系统设计。苹果对短语匹配应该也是有降权的,我们测试过一些词,得分应该是大于0.9的,就是影响不是特别大(国内的安卓市场可以明显发现,精准匹配比短语匹配高不少)。因此,苹果市场的“组词”,不应该刻意的追求,如果是重点保证的词,建议还是做“精准匹配”,一般的词,可以把有重复的词组合到一起,省一些位置,多加几个词。
当然,一个成功的APP推广案例是需要很多推广方式结合才能成功的。包括线上、线下推广,造势,付费推广等等手段。不同的开发商可以结合自身的情况来选择具体的推广方式。如果想了解更多APP海外推广方面的知识,请关注ASOtop1官网!
文/ASOtop1