A Famous Grid
Time Limit: 10000/3000 MS (Java/Others) Memory Limit: 32768/32768 K (Java/Others)
Total Submission(s): 365 Accepted Submission(s): 148
Problem Description
Mr. B has recently discovered the grid named "spiral grid".
Construct the grid like the following figure. (The grid is actually infinite. The figure is only a small part of it.)
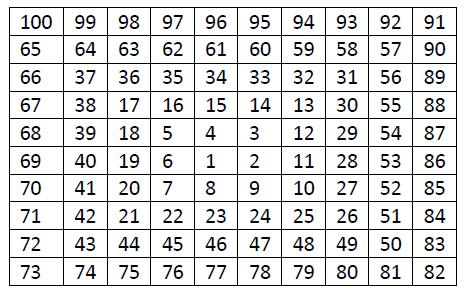
Considering traveling in it, you are free to any cell containing a composite number or 1, but traveling to any cell containing a prime number is disallowed. You can travel up, down, left or right, but not diagonally. Write a program to find the length of the shortest path between pairs of nonprime numbers, or report it's impossible.
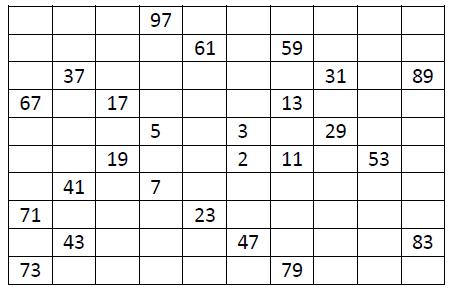
Construct the grid like the following figure. (The grid is actually infinite. The figure is only a small part of it.)

Considering traveling in it, you are free to any cell containing a composite number or 1, but traveling to any cell containing a prime number is disallowed. You can travel up, down, left or right, but not diagonally. Write a program to find the length of the shortest path between pairs of nonprime numbers, or report it's impossible.

Input
Each test case is described by a line of input containing two nonprime integer 1 <=x, y<=10,000.
Output
For each test case, display its case number followed by the length of the shortest path or "impossible" (without quotes) in one line.
Sample Input
1 4 9 32 10 12
Sample Output
Case 1: 1 Case 2: 7 Case 3: impossible
Source
题意应该很容易理解 就是一个蛇形的素数表里面 求两个合数的最短距离
一开始看错题了 以为是1000*1000 后来老吴说是10000*10000 的素数表格 直接做怕超时 所以也就直接放弃了 比赛完之后原来是100*100的表格
瞬间被晕死 虽然BFS没怎么学 但是这次写完之后也稍微有点提高了 继续努力吧 呵呵
 View Code
View Code
1 #include <iostream> 2 #include <fstream> 3 using namespace std; 4 #define max 210 5 #define fmax max*max 6 int p[max][max]; 7 int ss[max][max]; 8 int f[max*max]; 9 bool b[max*max]; 10 int dx[4]= {0, -1, 0, 1}; 11 int dy[4]= {1, 0, -1, 0}; 12 int x1[fmax],y1[fmax]; 13 14 void init() 15 { 16 // freopen("spiral.in","r",stdin); 17 //freopen("out.txt","w",stdout); 18 int sum=1; 19 int x=max/2,y=max/2,i,j; 20 p[x][y]=f[sum++]; 21 for ( i=1;i<max;i++) 22 { 23 for ( j=1;j<=i;j++) 24 { 25 if (i%2) 26 { 27 p[x][++y]=f[sum++]; 28 x1[sum-1]=x; 29 y1[sum-1]=y; 30 } 31 if (i%2==0) 32 { 33 p[x][--y]=f[sum++]; 34 x1[sum-1]=x; 35 y1[sum-1]=y; 36 } 37 } 38 for ( j=1;j<=i;j++) 39 { 40 if (i%2) 41 { 42 p[--x][y]=f[sum++]; 43 x1[sum-1]=x; 44 y1[sum-1]=y; 45 } 46 if (i%2==0) 47 { 48 p[++x][y]=f[sum++]; 49 x1[sum-1]=x; 50 y1[sum-1]=y; 51 } 52 } 53 } 54 } 55 56 void prim() 57 { 58 f[1]=1; 59 for (int i=2;i<max*max;i++) 60 { 61 f[i]=i; 62 if (!b[i]) 63 { 64 f[i]=0; 65 for (int j=i+i;j<max*max;j=j+i) 66 b[j]=1; 67 } 68 } 69 } 70 int ans; 71 int begin,end; 72 int q[fmax*2]; 73 int d[max][max]; 74 75 int bfs(int x,int y) 76 { 77 begin=end=0; 78 q[end++]=x1[x]; 79 q[end++]=y1[x]; 80 memset(d,-1,sizeof(d)); 81 d[x1[x]][y1[x]]=0; 82 while (begin<end) 83 { 84 int x2=q[begin++]; 85 int y2=q[begin++]; 86 if (p[x2][y2]==y) 87 return d[x2][y2]; 88 for (int i=0;i<4;i++) 89 { 90 int x3=x2+dx[i]; 91 int y3=y2+dy[i]; 92 if (x3>=0&&y3>=0&&x3<max&&y3<max&&p[x3][y3]&&d[x3][y3]==-1) 93 { 94 d[x3][y3]=d[x2][y2]+1; 95 q[end++]=x3; 96 q[end++]=y3; 97 } 98 } 99 } 100 return -1; 101 } 102 103 int main() 104 { 105 prim(); 106 init(); 107 int i,xx,yy,j; 108 /* for ( i=0;i<max;i++) 109 { 110 for (j=0;j<max;j++) 111 { 112 cout<<p[i][j]<<" "; 113 } 114 cout<<endl; 115 } 116 */ 117 int cas=1; 118 while (~scanf("%d%d",&xx,&yy)) 119 { 120 //printf("Case %d: ",cas++); 121 ans=0; 122 ans=bfs(xx,yy); 123 if (ans==-1) 124 { 125 printf("Case %d: impossible\n",cas++); 126 } 127 else printf("Case %d: %d\n",cas++,ans); 128 } 129 130 return 0; 131 }
